References
Mosayebi, P., Cobzas, D., Mutrtha A., and Jagersand
Tumor Invasion Margin on the Riemannian Space of Brain Fibers
,
Medical Image Analysis, 2011
Mosayebi P., Cobzas D., Jagersand M. and Murtha A.
Stability effects of finite difference methods on a mathematical tumor growth model
Mathematical Methods in Biomedical Image Analysis (MMBIA 2010), in conjunction with CVPR
Cobzas D., Mosayebi P., Murtha A. and Jagersand M.
Tumor invasion margin on the Riemannian space of brain fibers
International Conference on Medical Image Computing and Computer Assisted
Intervention (MICCAI) 2009
Description
Tumor growth prediction using a geodesic distance on the Riemannian space of brain fibers
Stability effects of finite difference methods on a mathematical tumor growth model
For more detailed description of the project at Parisa's MSc thesis webpage
Stability effects of finite difference methods on a mathematical tumor growth model
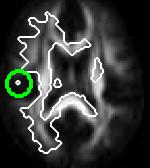
We investigated stability problems of some of the so far proposed finite difference methods for solving the anisotropic diffusion equation, a second order parabolic equation. This equation is used in a variety of applications in physics and image processing. Here, we focus on its usage in formulating brain tumor growth using the Diffusion Weighted Imaging (DWI) technique. Our study shows that the commonly used chain rule method to discretize diffusion equation is unstable. We propose a new 3D stable discretization method with its stability conditions to solve the diffusion equation. The new method uses directional discretization and forward differences. We also extend standard discretization method to 3D. The theoretical and practical comparisons of the three methods both on synthetic and real patient data show that while chain rule model is always unstable and standard discretization is unstable in theory, our proposed directional discretization is stable both in theory and practice.
Tumor growth prediction using a geodesic distance on the Riemannian space of brain fibers
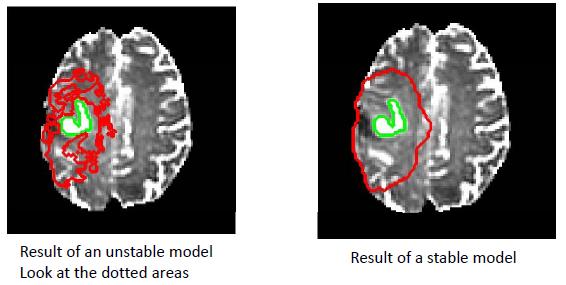
Gliomas are one of the most challenging tumors to treat or control locally. One of the main challenges is determining which areas of the apparently normal brain contain glioma cells, as gliomas are known to infiltrate for several centimeters beyond the clinically apparent lesion visualized on standard CT or MRI.
To ensure that radiation treatment encompasses the whole tumour, including the cancerous cells not revealed by MRI, doctors treat a volume of brain extending 2cm out from the margin of the visible tumour. This expanded volume often includes healthy, non-cancerous brain tissue.
Knowing that glioma cells preferentially spread along nerve fibers, we propose
the use of a geodesic distance on the Riemannian manifold of brain fibers to replace the Euclidean distance used in clinical practice and to correctly identify the tumor invasion margin. The novel model is directly driven by the particular patient DTI data. Furthermore, our method takes into account natural barriers to glioma growth such as the skull, the tentorium cerebelli and the falx cerebri.
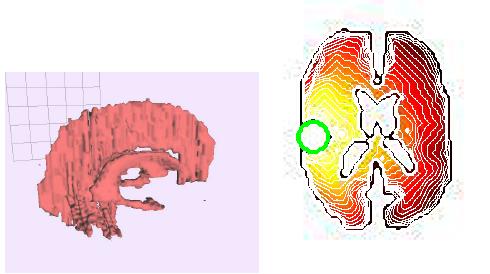
(left): barriers (right): geodesic distance ;
We tested our model on eight different patients by growing the tumor on the DWI scan of the patient and comparing the predicted distance with real growth shown on later MRI scans of the same patient. Comparative results of using Geodesic distance show an improvement vs. uniform (Euclidean) distance.
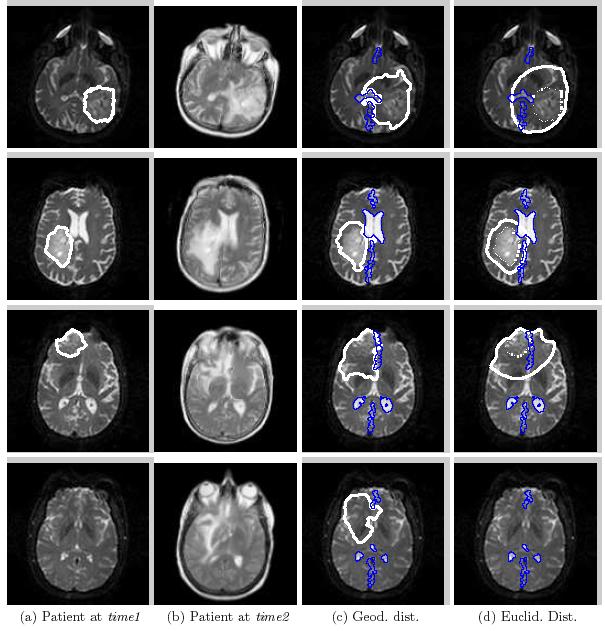
Comparative results for di erent patients of Geodesic (c) and Eu- clidean (d) simulated growth starting from segmented tumor at time1 (a) and linearly registered followed up scans at time2 (MRI-T2 or DWI) (b). Barriers are shown in blue.

Jaccard (overlap) scores for comparing registered ground truth with geodesic and Euclidean growth.
|
|