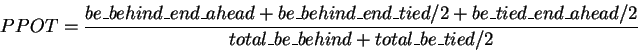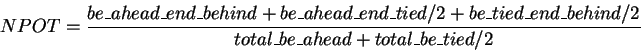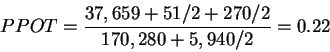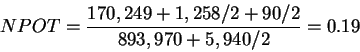


Next: Strategy
Up: Postflop
Previous: Postflop
To assess the quality of a hand after the flop,
the Hand Evaluator combines together
the strength and the potential of the hand in a value
called effective hand strength (EHS). The EHS is an estimate which gives
the probability that the given hand is currently the strongest one, or that
it will become the strongest one by the showdown with the next community cards (potential).
To calculate a hand's strength (HS) against a single opponent,
the Hand Evaluator enumerates all the possible
opponent hands and sums the weights of the hands that would win, lose or tie
the given hand. Recall that the weight of a hand is the probability that an
opponent would still be active with that particular hand.
For instance, assume that Loki's hole cards are A
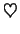 -8
-8
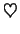 (the same as in the above preflop example), the community cards on the flop are
9
(the same as in the above preflop example), the community cards on the flop are
9
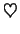 -8
-8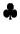 -2
-2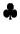 ,
and all weights are equal to 1 (uniform distribution).
From the
,
and all weights are equal to 1 (uniform distribution).
From the
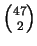 = 1081 possible opponent's two-card hands on the flop:
903 hands lose against Loki's hand, six hands tie and 172 hands defeat
Loki's3.1.
Therefore, Loki's HS is
= 1081 possible opponent's two-card hands on the flop:
903 hands lose against Loki's hand, six hands tie and 172 hands defeat
Loki's3.1.
Therefore, Loki's HS is
To extrapolate the hand strength value to
multiple opponents, the Hand Evaluator raises it to the power of the number of
opponents still active in the game (HSn). For the above example, if there
are four players active in the game (including Loki), the Hand Evaluator
calculates HS
n = (0.84)3 = 0.59.
The potential of a hand can be either positive or negative. Positive
potential (PPOT) is the probability of a hand becoming the strongest one when
it is behind. Negative potential (NPOT) is the probability of a hand
falling behind when it is ahead. Both potentials are
calculated by enumerating all possible opponents' hands and
community cards to come in the next rounds. Potential calculations on
the flop can be done by looking ahead either one round (considering the
45 possible cards on the turn) or two rounds (considering the
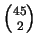 =990possible two-card combinations on the river). PPOT is calculated by adding
the weights of the cases where Loki's hand improves.
=990possible two-card combinations on the river). PPOT is calculated by adding
the weights of the cases where Loki's hand improves.
NPOT is given by:
Consider the same above example. Table 3.1 shows the number of cases where
Loki's hand situation
at the flop changes (or remains the same) by the time the other two community cards are
dealt. Assuming uniform weights, this table shows the
sum of the weights of all the cases.
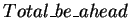 is equal to
the number of cases where Loki's hand on the flop is the strongest one multiplied by
the number of possible next two-card combinations (
903 * 990
= 893,970).
is equal to
the number of cases where Loki's hand on the flop is the strongest one multiplied by
the number of possible next two-card combinations (
903 * 990
= 893,970).
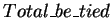 is 5,940 (6 * 990) and
is 5,940 (6 * 990) and
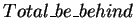 is 170,280
(172 * 990). The total number of cases enumerated in the potential
calculations is
1081 * 990 = 1,070,190. Thus, PPOT for Loki's hand (A
is 170,280
(172 * 990). The total number of cases enumerated in the potential
calculations is
1081 * 990 = 1,070,190. Thus, PPOT for Loki's hand (A
 -8
-8
 )
is
)
is
and NPOT is :
Table 3.1:
Number of cases where Loki's hand situation changes after two community
cards are dealt
| Flop's situation |
River's situation |
Number of cases |
| |
Ahead |
722,463 |
| Ahead |
Behind |
170,249 |
| |
Tied |
1,258 |
| |
Ahead |
37,659 |
| Behind |
Behind |
132,570 |
| |
Tied |
51 |
| |
Ahead |
270 |
| Tied |
Behind |
90 |
| |
Tied |
5,580 |
|



Next: Strategy
Up: Postflop
Previous: Postflop
Lourdes Pena
1999-09-10
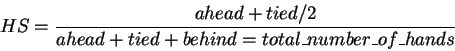
![]() =990possible two-card combinations on the river). PPOT is calculated by adding
the weights of the cases where Loki's hand improves.
=990possible two-card combinations on the river). PPOT is calculated by adding
the weights of the cases where Loki's hand improves.