 |
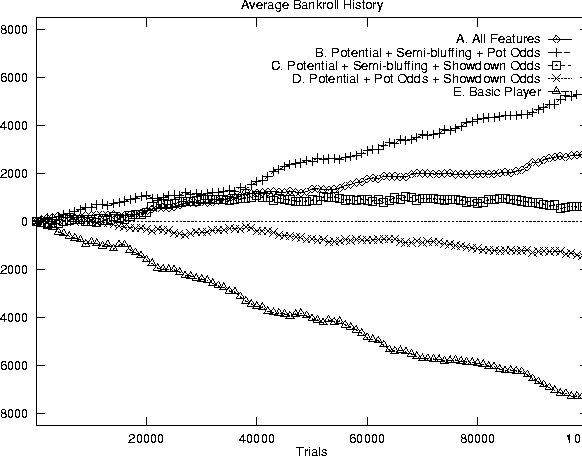
As a sample self-play experiment, we have tested five different versions of Loki together, using different components of the betting strategy, for a 10,000 hand tournament (100,000 trials). We use the average bankroll of the two copies of each version as a metric for performance. The results can be seen in Figure 8.1 (note this is with a 2-4 betting structure). Player A used the entire betting strategy, and B, C, and D each lacked a particular feature (B did not use showdown odds, C did not use pot odds, and D did not use semi-bluffing). Finally, player E used the simple betting strategy from Figure 6.2 (only HSn is used). All five versions used a moderate tightness level, and generic opponent modeling to ensure reasonable weights.
This experiment reveals the danger of over-interpreting self-play simulations. It suggests that every feature except showdown odds is a gain, especially semi-bluffing. Player B won the tournament by a large margin suggesting that Loki is better off without the showdown odds feature. However, in practice this is often not the case. For example, in one long IRC session (4857 games) against a variety of human opponents, showdown odds were considered 883 times and used to call and continue playing 123 times. In these games, Loki later folded 30 times for a total cost of $108 (scaled to a betting structure of 2-4), won 6 games without a showdown, and won 37 of the 87 remaining hands that went to a showdown. The total winnings were $1221 and the total cost (of the initial call and later betting actions) was $818. Thus, the EV of showdown odds was a net gain of $3.28 per decision, or 1.64 small bets (the EV of a folding decision is $0 since there is no cost and there are no winnings). Although this was a good session, the EV for this feature was consistently positive in other sessions. In a longer set of 12,192 games, it was $0.72 per decision (or 0.36 small bets). Although the performance after the decision point is dependent on the performance of the betting strategy overall, Loki would have netted $0 in these situations, instead of a consistent gain, without showdown odds.
Showdown odds was originally added because Loki often over-estimated what its IRC opponents were holding. Bets were taken too seriously and EHS' would be just under the betting threshold. With showdown odds we will typically decide to play a hand which has a PPOT that is just under the calling threshold and an EHS' that is just under the betting threshold. When Loki over-estimates its opponents, showdown odds is usually a gain. However, in self-play, because it plays a very tight game (the other extreme), a bet is not taken seriously enough (EHS' is too high). So when we decide to play the showdown odds it is often a mistake. However, it will be profitable in an environment where opponents are frequently bluffing or otherwise betting too much.
To see the reverse of this effect (showdown odds as a winner in self-play), Figure 8.2 shows the results from an experiment between two copies of A (all features), two copies of B (no showdown odds), and six copies of BPL'. BPL (``Best Player Loose") is a loose non-modeling player, who uses all features of the betting strategy but with reduced thresholds for looser play. This player also uses a fixed weight array for all opponents regardless of their actions (since it performs no re-weighting, a ``reasonable" set of weights is much more realistic than uniform weights). BPL' is the same as BPL, except it ignores the number of opponents (uses HS1 instead of HSn in EHS calculations) for much more aggressive play. In this experiment, it is clear that using showdown odds resulted in a significant performance gain, although both A and B had a large advantage over BPL'.
Because we recognize that the present betting strategy is a potential limitation and is in need of re-designing, we are not particularly interested in the value of each particular feature. Since showdown odds is theoretically a gain (positive expected value) when the weights are accurate, this experiment shows the limitations of the present system and reinforces the need for good opponent modeling. The main focus of our experimentation is to examine the benefits and problems of opponent modeling, including the difference between generic and specific modeling.