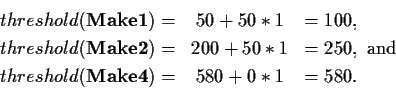


Next: 6.2 Basic Post-Flop Betting
Up: 6. Betting Strategy
Previous: 6. Betting Strategy
Contents
6.1 Pre-Flop Betting Strategy
The implemented pre-flop betting strategy is preliminary and makes
use of expert information. It is sophisticated enough to not hamper
overall performance so that the focus can be put on post-flop
play (the more interesting
portion of the game). Loki examines several variables, uses
the expert knowledge to determine thresholds for various betting
actions, and chooses a strategy:
- Make0: fold if it costs more than zero to continue
playing, otherwise check.
- Call1: fold if it costs two or more bets to continue
(and we have not already voluntarily put money in the pot this round),
otherwise check/call.
- Make1: like Call1 except bet if there has not
been a bet this round (with the big blind this cannot happen
in the pre-flop).
- Call2: always call/check (despite what the name of
this strategy suggests, even more than 2 bets).
- Make2: bet/raise if less than two bet/raises have been made
this round, otherwise call.
- Make4: bet/raise until the betting is capped, otherwise call.
Except for the small blind, which is given special treatment,
Call1 and Call2 are effectively not used, so there are really only 4
different strategies. Once a strategy is selected it is fixed for
all subsequent actions in the pre-flop. The small blind is a
special case due to only having
to call one half of a bet (so Call1 is really Call0.5 and
Call2 is really Call1.5), and has fixed thresholds for these
two strategies.
Call1 (and hence Make1) has a special case folding requirement,
that ``we have not already voluntarily put money in the pot this round."
This is a feature added after testing with human opponents on IRC.
Many players were
very aggressive and would raise frequently. This meant that often
when Loki called the blind with a decent hand (but not Call2 or
better), two or more players would then raise, causing Loki to fold.
Due to this commonly exploited weakness, the kludge is necessary
until some amount of opponent of modeling is implemented into the pre-flop.
The thresholds for selecting a betting strategy
are determined from a set of linear formulas of the form
|
threshold(strategy) = base + increment * position
|
(6.1) |
where strategy is the betting strategy ( e.g. Make1),
base and increment are defined by a human expert (see Appendix
B), and
position is the number of players to act before it is
the small blind's turn again (so, if 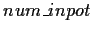 is the number of
players still in the pot, the small blind is position
is the number of
players still in the pot, the small blind is position
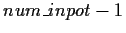 ,
the big blind is position
,
the big blind is position
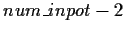 ,
the first player to
act is position
,
the first player to
act is position
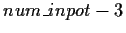 and so on, until the button (dealer)
who is position 0).
and so on, until the button (dealer)
who is position 0).
For example, if Loki is playing tight
against 3-4 players, the [ base, increment] values used for
Make2 are [200,50] (based on Table B.1)
so the formula used is
based on Equation 6.1.
That is, the coefficients used for the linear formula depend
on both the variable (group) and the parameter (tightness).
The variable group is based on the expected number of players
(
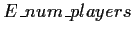 ), which is
), which is
There are three cases of interest for the expected
number of players. We round
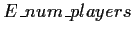 to the
nearest integer and determine the appropriate group based on what
range that value falls in: ``2 players", ``3-4 players" and ``5 or more
players" (see Appendix B).
The state variable
to the
nearest integer and determine the appropriate group based on what
range that value falls in: ``2 players", ``3-4 players" and ``5 or more
players" (see Appendix B).
The state variable
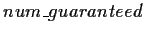 is the number of players
who have already put money in the pot (and have presumably committed
to playing). This includes the blinds as well as ourselves (we assume
we will play).
is the number of players
who have already put money in the pot (and have presumably committed
to playing). This includes the blinds as well as ourselves (we assume
we will play).
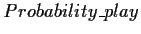 is an expert-defined value for the average playing percentage of
players (by default 0.60). Appropriate opponent modeling
would provide much better estimates for this value, based on
the observation of the current session .
is an expert-defined value for the average playing percentage of
players (by default 0.60). Appropriate opponent modeling
would provide much better estimates for this value, based on
the observation of the current session .
The parameter tightness is a setting which affects the
percentage of hands that Loki will play (indirectly, by selecting
a different set of thresholds). The
three settings are tight, moderate, and loose (the default).
With ten players these roughly translate into playing 18%, 21% and
24% of all hands (the distinction is not large so the terms
are a misnomer - all levels are relatively conservative).
There is one [base, increment] pair per set of
group, strategy and tightness values (Table B.1)
so there are 27 pairs total (since Make0 is
the default strategy only three thresholds are needed for determining
the strategy). Once the thresholds are determined, the actual strategy
selected is dependent on the pre-calculated income rate (IR) of the
hole cards.
Figure 6.1 describes the algorithm for selecting a strategy.
For example, consider a six player game.
We hold A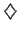 -T
-T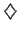 and are playing tight.
The first two players put in blinds, the next two fold, and it
is Loki's turn.
There is still one player, the button, who has not yet acted.
So position = 1,
and are playing tight.
The first two players put in blinds, the next two fold, and it
is Loki's turn.
There is still one player, the button, who has not yet acted.
So position = 1,
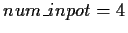 and
and
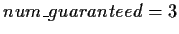 (including
Loki). We then calculate
(including
Loki). We then calculate
and use this to determine group = ``3-4 players".
Then, using Table B.1 we calculate
Finally, we find the value of our hand is IR = 491 and
select the appropriate strategy. Since
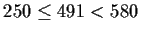 ,
we select the Make2 strategy, and raise.
,
we select the Make2 strategy, and raise.
Figure 6.1:
Pre-Flop Betting Strategy
 |



Next: 6.2 Basic Post-Flop Betting
Up: 6. Betting Strategy
Previous: 6. Betting Strategy
Contents
Denis Papp
1998-11-30
![]() ), which is
), which is
![]() -T
-T![]() and are playing tight.
The first two players put in blinds, the next two fold, and it
is Loki's turn.
There is still one player, the button, who has not yet acted.
So position = 1,
and are playing tight.
The first two players put in blinds, the next two fold, and it
is Loki's turn.
There is still one player, the button, who has not yet acted.
So position = 1,
![]() and
and
![]() (including
Loki). We then calculate
(including
Loki). We then calculate