In practice, hand strength alone is insufficient to assess the quality
of a hand.
Hand potential assesses the probability of the hand improving
(or being overtaken) as additional community cards appear.
Consider the hand 8![]() -7
-7![]() with a flop of 9
with a flop of 9![]() -6
-6![]() -2
-2![]() .
The probability of having the strongest hand is very low,
even against one random opponent (11.5%).
On the other hand, there is tremendous potential for improvement.
With two cards yet to come, any
.
The probability of having the strongest hand is very low,
even against one random opponent (11.5%).
On the other hand, there is tremendous potential for improvement.
With two cards yet to come, any ![]() ,
10, or 5 will give us a flush
or a straight. Hence there is a high probability that
this hand will improve substantially in strength, so the hand has a lot
of value. We need to be aware of how the potential affects hand strength.
,
10, or 5 will give us a flush
or a straight. Hence there is a high probability that
this hand will improve substantially in strength, so the hand has a lot
of value. We need to be aware of how the potential affects hand strength.
This example describes positive potential (PPOT): the probability of pulling ahead when we are behind. We can also compute the negative potential (NPOT): the probability of falling behind given we are ahead. Both of these can be computed by enumeration in real-time. We have 1,081 possible subcases (opposing hands for which we have weights) on the flop and 990 on the turn. For each subcase we can either do a two card look-ahead (consider the 990 combinations of the next two cards on the flop) or a one card look-ahead (45 cards on the flop and 44 on the turn). For each subcase we count how many combinations of upcoming cards result in us being ahead, behind or tied. The total number of cases to be considered is:
The potential for A![]() -Q
-Q![]() /3
/3![]() -4
-4![]() -J
-J![]() with
uniform weighting is shown in Table 5.1. The table shows what
the result would be after seven cards,
for cases where we are ahead, tied or behind after five cards.
For example, if we did not have the
best hand after five cards, then there are 91,981 combinations of cards
(pre-flop and two cards to come) for the opponents that will give
us the best hand. Of the remaining hands, 1,036 will leave us tied
with the best hand, and 346,543 will leave us behind. In other words,
if we are behind we have roughly a
PPOT2 = 21% chance of
winning against one opponent in a showdown.
Additionally, if we are currently ahead and that opponent
plays to the showdown, we have roughly a
NPOT2 = 27% chance of
losing.
with
uniform weighting is shown in Table 5.1. The table shows what
the result would be after seven cards,
for cases where we are ahead, tied or behind after five cards.
For example, if we did not have the
best hand after five cards, then there are 91,981 combinations of cards
(pre-flop and two cards to come) for the opponents that will give
us the best hand. Of the remaining hands, 1,036 will leave us tied
with the best hand, and 346,543 will leave us behind. In other words,
if we are behind we have roughly a
PPOT2 = 21% chance of
winning against one opponent in a showdown.
Additionally, if we are currently ahead and that opponent
plays to the showdown, we have roughly a
NPOT2 = 27% chance of
losing.
If Trow,col refers to the values in the table (for brevity we use B, T, A, and S for Behind, Tied, Ahead, and Sum) then PPOT2 and NPOT2 are calculated by:
Figure 5.2 describes the algorithm for two card look-ahead
from the flop. The parameter w is, as for Figure
5.1, for the weight array of the opponent
(opponent modeling is discussed later), and can simply be a uniform
set of weights.
The HandStrength calculation is easily embedded
within this function, and the one card look-ahead function HandPotential1
is essentially the same as HandPotential2.
In this function, the inner loop is executed
![]() times and so the
Rank function is called
times and so the
Rank function is called
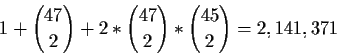
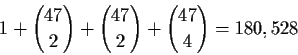
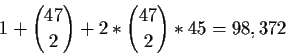
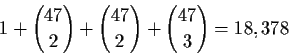
In Table 5.1 we compute the
potential based on two additional cards and it produces
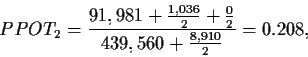 |
(5.7) |
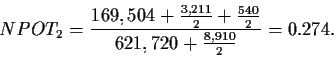 |
(5.8) |