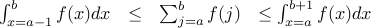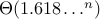algorithms: prologue
Aryabhata
---------
\/ 8 0 1 2 3 = ? (say to 2 decimal places)
2 8 3 . 0 6 <- x
-------------------
\/ 0 8 0 1 2 3.0 0 0 0 <- n
2 4
---
4 0 1
48 3 8 4
-----
1 7 2 3
563 1 6 8 9
-------
3 4 0 0
5660
-------
3 4 0 0 0 0
56606 3 3 9 6 3 6
-----------
3 6 4 <- r
... so n = x*x + 0.0364
------------------
\/ 1 1 0 1 0 1 1 0 1 = ?
1 0 1 0 0 <- x
--------------------
\/ 0 1 1 0 1 0 1 1 0 1 <- n
1 1
---
0 1 0
100
-----
1 0 1 0
1001 1 0 0 1
-------
1 1 1
10100
-----
1 1 1 0 1
101000
---------
1 1 1 0 1 <- r
... so n = x*x + r
Al Khwarizmi
Fibonacci
import time
def fib(n):
if (n<=1):
return n
return fib(n-1) + fib(n-2)
t1 = 1.0
for n in range(100):
now, fn = time.time(), fib(n)
t0, t1 = t1, time.time()-now
print n, fn, t1, "sec, ratio current/prev", t1/t0
estimating runtime
test for runtime in
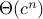 :
:say
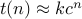
then
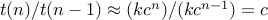
test for runtime in
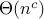 :
:say
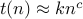
then
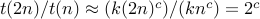
e.g. if
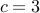 then
then 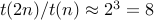
test for runtime in
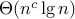 :
:say
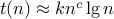
then
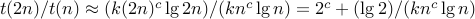
e.g. if
 then
then 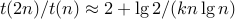
method 1: experiment
execute program, looks like run time in
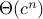 where
where 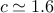
method 2: use theory to estimate
count basic operations as function of n
e.g. count only procedure calls
C(n): number of procedure calls to execute fib(n)
fib(0): only call is fib(0), so C(0) is 1
fib(1): only call is fib(1), so C(1) is 1
fib(2): also calls fib(1), fib(0), so C(2) is 3
for n
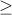 2, C(n)
2, C(n)  1
1 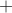 C(n-1)
C(n-1) 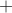 C(n-2)
C(n-2)
prove by induction: T(n) > f(n)
prove T(n) in
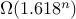
prove by induction: C(n) > f(n)
prove C(n) in
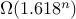
pick one: recursive fibonacci computation is
easy to prove correctness ?
infeasible for
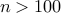 ?
?easy to implement quickly ?
all of the above ?
how to do better ?
write/read instead of recompute (memoization)
def ifib(n):
a,b = 0,1
for _ in range(n):
a, b = b, a+b #
return a
x = 40000
for _ in range(6):
now = time.time()
fx = ifib(x)
print x, time.time() - now, "sec"
x *= 2
I(n): number of #-line executions in ifib(n)
I(n) in
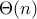 (why?)
(why?)run the above program: roughly, what is time( ifib(2x) ) / time ( ifib(x) ) ?
what does this suggest about runtime of ifib(n) ?
on average, how long does one #-line execution take?
O(1) time ?
O(lg n) time ?
O(n ) time ?
all of the above ?
so runtime of ifib(n) is
in O(n) ?
in O(n lg n) ?
in O(n^2) ?
all of the above ?
big O
f(n) ∈ O( g(n) ) means
f(n), g(n) are functions from positive integers to positive reals
for some positive real constant c, for some positive integer n0, for all positive integers n ≥ n0, f(n) ≤ c g(n)
synonyms
f ∈ O( g )
f(n) = O( g(n) )
f = O( g )
f ∈ Ω( g ) means g ∈ O ( f )
f ∈ Θ( g ) means f ∈ O ( g ) and f ∈ Ω( g )
f(n) ∈ o( g(n) ) means
limit, as n gets large, of f(n)/g(n) = 0
so there is no positive constant c such that f(n) > c g(n) for all n > 0,
so f ∉ Ω( g )
synonyms
f ∈ o( g )
f = o( g )
f(n) = o( g(n) )
c positive constant, f(n) = c g(n) then Θ( f ) = Θ( g )
f(n) ∈ O( g(n) ) then Θ( f(n) + g(n) ) = Θ( g )
if f ∈ o (g) then
f ∈ O( g )
f ∉ Ω( g )
constants 0 < a < b then na ∈ o( nb )
constants 0 < a, 1 < b then na ∈ o( bn )
constants 0 < a,b then (log n)a ∈ o( nb )
L'Hopital's rule
for integer
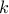 , let
, let 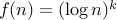
for positive real
 , let
, let 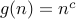
show
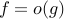
hint: use L'Hopital's rule
for increasing function
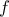 ,
,