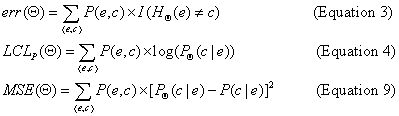This webpage presents a number of results related to the paper
"Structural
Extension to Logistic Regression:
Discriminative Parameter Learning of Belief Net Classifiers"
(ps; pdf),
which appears in
the Machine Learning Journal
special issue on
Probabilistic
Graphical Models for Classification
-- MLJ 59(3), June 2005, p. 297--322.
The bulk of the material in this website also appears in
ps
and
pdf
format.
Report a problem
in this page
We evaluated various algorithms over the standard 25
benchmark datasets used by Friedman et al. [FGG97]: 23 from UCI
repository [BM00], plus “mofn-3-7-10” and “corral”, which were developed by
[KJ97] to study feature selection. Also the same 5-fold
cross validation and Train/Test learning schemas are followed (see
following Table). As part of data preparation, continuous
data are always discretized using the supervised entropy-based approach.
(You can download the discretized data
here.)
| Data set |
|
# Attributes |
# Classes |
# Instances |
| |
|
|
|
Train |
Test |
| 1 |
australian |
14 |
2 |
690 |
CV-5 |
| 2 |
breast |
10 |
2 |
683 |
CV-5 |
| 3 |
chess |
36 |
2 |
2130 |
1066 |
| 4 |
cleve |
13 |
2 |
296 |
CV-5 |
| 5 |
corral |
6 |
2 |
128 |
CV-5 |
| 6 |
crx |
15 |
2 |
653 |
CV-5 |
| 7 |
diabetes |
8 |
2 |
768 |
CV-5 |
| 8 |
flare |
10 |
2 |
1066 |
CV-5 |
| 9 |
german |
20 |
2 |
1000 |
CV-5 |
| 10 |
glass |
9 |
7 |
214 |
CV-5 |
| 11 |
glass2 |
9 |
2 |
163 |
CV-5 |
| 12 |
heart |
13 |
2 |
270 |
CV-5 |
| 13 |
hepatitis |
19 |
2 |
80 |
CV-5 |
| 14 |
iris |
4 |
3 |
150 |
CV-5 |
| 15 |
letter |
16 |
26 |
15000 |
5000 |
| 16 |
lymphography |
18 |
4 |
148 |
CV-5 |
| 17 |
mofn-3-7-10 |
10 |
2 |
300 |
1024 |
| 18 |
pima |
8 |
2 |
768 |
CV-5 |
| 19 |
satimage |
36 |
6 |
4435 |
2000 |
| 20 |
segment |
19 |
7 |
1540 |
770 |
| 21 |
shuttle-small |
9 |
7 |
3866 |
1934 |
| 22 |
soybean-large |
35 |
19 |
562 |
CV-5 |
| 23 |
vehicle |
18 |
4 |
846 |
CV-5 |
| 24 |
vote |
16 |
2 |
435 |
CV-5 |
| 25 |
waveform-21 |
21 |
3 |
300 |
4700 |
Description of data sets used in the experiments; see also [FGG97:
N. Friedman, D. Geiger and M. Goldszmidt. Bayesian Network
Classifiers. Machine Learning 29:131-163, 1997 ]
Top
|
|
Data set |
NB+OFE |
|
NB+ELR |
|
TAN+OFE |
TAN+ELR |
|
GBN+OFE |
|
GBN+ELR |
|
|
1 |
australian |
86.81 |
± |
0.84 |
84.93 |
± |
1.06 |
84.93 |
± |
1.03 |
84.93 |
± |
1.03 |
86.38 |
± |
0.98 |
86.81 |
± |
1.11 |
|
2 |
breast |
97.21 |
± |
0.75 |
96.32 |
± |
0.66 |
96.32 |
± |
0.81 |
96.32 |
± |
0.70 |
96.03 |
± |
0.50 |
95.74 |
± |
0.43 |
|
3 |
chess |
87.34 |
± |
1.02 |
95.40 |
± |
0.64 |
92.40 |
± |
0.81 |
97.19 |
± |
0.51 |
90.06 |
± |
0.92 |
90.06 |
± |
0.92 |
|
4 |
cleve |
82.03 |
± |
2.66 |
81.36 |
± |
2.46 |
80.68 |
± |
1.75 |
81.36 |
± |
1.78 |
84.07 |
± |
1.48 |
82.03 |
± |
1.83 |
|
5 |
corral |
86.40 |
± |
5.31 |
86.40 |
± |
3.25 |
93.60 |
± |
3.25 |
100.00 |
± |
0.00 |
100.00 |
± |
0.00 |
100.00 |
± |
0.00 |
|
6 |
crx |
86.15 |
± |
1.29 |
86.46 |
± |
1.85 |
86.15 |
± |
1.70 |
86.15 |
± |
1.70 |
86.00 |
± |
1.94 |
85.69 |
± |
1.30 |
|
7 |
diabetes |
74.77 |
± |
1.05 |
75.16 |
± |
1.39 |
74.38 |
± |
1.35 |
73.33 |
± |
1.97 |
75.42 |
± |
0.61 |
76.34 |
± |
1.30 |
|
8 |
flare |
80.47 |
± |
1.03 |
82.82 |
± |
1.35 |
83.00 |
± |
1.06 |
83.10 |
± |
1.29 |
82.63 |
± |
1.28 |
82.63 |
± |
1.28 |
|
9 |
german |
74.70 |
± |
0.80 |
74.60 |
± |
0.58 |
73.50 |
± |
0.84 |
73.50 |
± |
0.84 |
73.70 |
± |
0.68 |
73.70 |
± |
0.68 |
|
10 |
glass |
47.62 |
± |
3.61 |
44.76 |
± |
4.22 |
47.62 |
± |
3.61 |
44.76 |
± |
4.22 |
47.62 |
± |
3.61 |
44.76 |
± |
4.22 |
|
11 |
glass2 |
81.25 |
± |
2.21 |
81.88 |
± |
3.62 |
80.63 |
± |
3.34 |
80.00 |
± |
3.90 |
80.63 |
± |
3.75 |
78.75 |
± |
3.34 |
|
12 |
heart |
78.52 |
± |
3.44 |
78.89 |
± |
4.08 |
78.52 |
± |
4.29 |
78.15 |
± |
3.86 |
79.63 |
± |
3.75 |
78.89 |
± |
4.17 |
|
13 |
hepatitis |
83.75 |
± |
4.24 |
86.25 |
± |
5.38 |
88.75 |
± |
4.15 |
85.00 |
± |
5.08 |
90.00 |
± |
4.24 |
90.00 |
± |
4.24 |
|
14 |
iris |
92.67 |
± |
2.45 |
94.00 |
± |
2.87 |
92.67 |
± |
2.45 |
92.00 |
± |
3.09 |
92.00 |
± |
3.09 |
92.00 |
± |
3.09 |
|
15 |
letter |
72.40 |
± |
0.63 |
83.02 |
± |
0.53 |
83.22 |
± |
0.53 |
88.90 |
± |
0.44 |
79.78 |
± |
0.57 |
81.21 |
± |
0.55 |
|
16 |
lymphography |
82.76 |
± |
1.89 |
86.21 |
± |
2.67 |
86.90 |
± |
3.34 |
84.83 |
± |
5.18 |
79.31 |
± |
2.18 |
78.62 |
± |
2.29 |
|
17 |
mofn-3-7-10 |
86.72 |
± |
1.06 |
100.00 |
± |
0.00 |
91.60 |
± |
0.87 |
100.00 |
± |
0.00 |
86.72 |
± |
1.06 |
100.00 |
± |
0.00 |
|
18 |
pima |
75.03 |
± |
2.45 |
75.16 |
± |
2.48 |
74.38 |
± |
2.81 |
74.38 |
± |
2.58 |
75.03 |
± |
2.25 |
74.25 |
± |
2.53 |
|
19 |
satimage |
81.55 |
± |
0.87 |
85.40 |
± |
0.79 |
88.30 |
± |
0.72 |
88.30 |
± |
0.72 |
79.25 |
± |
0.91 |
79.25 |
± |
0.91 |
|
20 |
segment |
85.32 |
± |
1.28 |
89.48 |
± |
1.11 |
89.35 |
± |
1.11 |
89.22 |
± |
1.12 |
77.53 |
± |
1.50 |
77.40 |
± |
1.51 |
|
21 |
shuttle-small |
98.24 |
± |
0.30 |
99.12 |
± |
0.21 |
99.12 |
± |
0.21 |
99.22 |
± |
0.20 |
97.31 |
± |
0.37 |
97.88 |
± |
0.33 |
|
22 |
soybean-large |
90.89 |
± |
1.31 |
90.54 |
± |
0.54 |
93.39 |
± |
0.67 |
92.86 |
± |
1.26 |
82.50 |
± |
1.40 |
85.54 |
± |
0.99 |
|
23 |
vehicle |
55.98 |
± |
0.93 |
64.14 |
± |
1.28 |
65.21 |
± |
1.32 |
66.39 |
± |
1.22 |
48.52 |
± |
2.13 |
51.95 |
± |
1.32 |
|
24 |
vote |
90.34 |
± |
1.44 |
95.86 |
± |
0.78 |
93.79 |
± |
1.18 |
95.40 |
± |
0.63 |
96.32 |
± |
0.84 |
95.86 |
± |
0.78 |
|
25 |
waveform-21 |
75.91 |
± |
0.62 |
78.55 |
± |
0.60 |
76.30 |
± |
0.62 |
76.30 |
± |
0.62 |
65.79 |
± |
0.69 |
65.79 |
± |
0.69 |
Top
|
|
Data set |
NB+ELR |
NB+APN |
NB+EM |
|
TAN+ELR |
TAN+APN |
TAN+EM |
GBN+ELR |
GBN+APN |
GBN+EM |
|
1 |
australian |
78.41 |
± |
1.01 |
78.41 |
± |
0.96 |
78.55 |
± |
1.01 |
77.25 |
± |
0.59 |
78.12 |
± |
0.74 |
77.25 |
± |
0.59 |
74.06 |
± |
1.06 |
74.06 |
± |
1.06 |
74.78 |
± |
0.74 |
|
2 |
breast |
95.59 |
± |
1.32 |
96.03 |
± |
1.20 |
96.03 |
± |
1.20 |
96.03 |
± |
1.13 |
95.88 |
± |
0.95 |
96.18 |
± |
1.02 |
94.12 |
± |
1.63 |
94.85 |
± |
1.36 |
94.85 |
± |
1.36 |
|
3 |
chess |
94.56 |
± |
0.69 |
89.59 |
± |
0.94 |
89.68 |
± |
0.93 |
96.15 |
± |
0.59 |
93.90 |
± |
0.73 |
94.09 |
± |
0.72 |
90.34 |
± |
0.90 |
90.06 |
± |
0.92 |
90.06 |
± |
0.92 |
|
4 |
cleve |
84.07 |
± |
1.90 |
82.03 |
± |
2.05 |
82.03 |
± |
2.05 |
83.73 |
± |
1.57 |
83.73 |
± |
1.57 |
83.73 |
± |
1.57 |
83.05 |
± |
1.93 |
81.36 |
± |
2.34 |
83.39 |
± |
1.89 |
|
5 |
corral |
81.60 |
± |
3.25 |
83.20 |
± |
3.67 |
83.20 |
± |
3.67 |
88.80 |
± |
3.67 |
90.40 |
± |
1.60 |
88.80 |
± |
2.65 |
92.00 |
± |
1.79 |
88.80 |
± |
2.65 |
92.00 |
± |
1.79 |
|
6 |
crx |
87.54 |
± |
1.43 |
86.00 |
± |
1.67 |
86.00 |
± |
1.67 |
85.85 |
± |
1.43 |
84.62 |
± |
1.29 |
85.85 |
± |
1.43 |
86.15 |
± |
1.67 |
87.23 |
± |
1.10 |
86.92 |
± |
0.97 |
|
7 |
diabetes |
75.42 |
± |
1.84 |
74.64 |
± |
1.83 |
74.64 |
± |
1.83 |
74.64 |
± |
2.06 |
74.90 |
± |
2.19 |
74.90 |
± |
2.19 |
73.46 |
± |
1.99 |
73.20 |
± |
1.99 |
72.81 |
± |
1.79 |
|
8 |
flare |
83.00 |
± |
1.42 |
82.35 |
± |
1.21 |
82.44 |
± |
1.24 |
82.54 |
± |
0.86 |
82.35 |
± |
1.90 |
82.54 |
± |
1.52 |
82.63 |
± |
1.28 |
82.63 |
± |
1.28 |
82.63 |
± |
1.28 |
|
9 |
german |
74.50 |
± |
0.89 |
74.10 |
± |
1.09 |
74.00 |
± |
1.05 |
72.70 |
± |
0.54 |
74.00 |
± |
0.97 |
72.90 |
± |
0.40 |
73.70 |
± |
0.68 |
73.40 |
± |
0.86 |
73.70 |
± |
0.68 |
|
10 |
glass |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
35.71 |
± |
4.33 |
|
11 |
glass2 |
79.38 |
± |
3.22 |
77.50 |
± |
3.03 |
77.50 |
± |
3.03 |
76.25 |
± |
2.72 |
76.25 |
± |
3.37 |
76.25 |
± |
2.72 |
78.13 |
± |
3.28 |
77.50 |
± |
3.75 |
78.13 |
± |
3.28 |
|
12 |
heart |
75.19 |
± |
5.13 |
74.81 |
± |
4.63 |
74.81 |
± |
4.63 |
72.22 |
± |
3.26 |
73.33 |
± |
4.00 |
73.33 |
± |
4.00 |
73.70 |
± |
3.95 |
73.33 |
± |
4.37 |
73.33 |
± |
4.37 |
|
13 |
hepatitis |
81.25 |
± |
7.65 |
86.25 |
± |
5.00 |
86.25 |
± |
5.00 |
82.50 |
± |
5.00 |
87.50 |
± |
3.95 |
86.25 |
± |
5.00 |
86.25 |
± |
3.64 |
86.25 |
± |
3.64 |
86.25 |
± |
3.64 |
|
14 |
iris |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
94.67 |
± |
0.82 |
|
15 |
letter |
75.28 |
± |
0.61 |
67.24 |
± |
0.66 |
67.14 |
± |
0.66 |
81.86 |
± |
0.54 |
85.25 |
± |
0.50 |
84.07 |
± |
0.52 |
72.80 |
± |
0.63 |
69.81 |
± |
0.65 |
68.60 |
± |
0.66 |
|
16 |
lymphography |
84.83 |
± |
2.80 |
84.14 |
± |
1.38 |
83.45 |
± |
1.29 |
82.07 |
± |
3.84 |
78.62 |
± |
2.01 |
81.38 |
± |
3.87 |
78.62 |
± |
2.29 |
78.62 |
± |
2.29 |
79.31 |
± |
2.18 |
|
17 |
mofn-3-7-10 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
82.03 |
± |
1.20 |
|
18 |
pima |
74.90 |
± |
2.85 |
74.90 |
± |
2.85 |
74.90 |
± |
2.85 |
74.25 |
± |
2.45 |
73.99 |
± |
2.28 |
73.99 |
± |
2.28 |
73.99 |
± |
2.06 |
74.64 |
± |
2.25 |
74.77 |
± |
2.31 |
|
19 |
satimage |
84.90 |
± |
0.80 |
81.85 |
± |
0.86 |
81.90 |
± |
0.86 |
87.70 |
± |
0.73 |
87.80 |
± |
0.73 |
87.70 |
± |
0.73 |
73.95 |
± |
0.98 |
76.35 |
± |
0.95 |
76.30 |
± |
0.95 |
|
20 |
segment |
89.74 |
± |
1.09 |
85.19 |
± |
1.28 |
85.19 |
± |
1.28 |
89.35 |
± |
1.11 |
89.22 |
± |
1.12 |
89.09 |
± |
1.12 |
77.40 |
± |
1.51 |
77.40 |
± |
1.51 |
77.40 |
± |
1.51 |
|
21 |
shuttle-small |
99.17 |
± |
0.21 |
99.07 |
± |
0.22 |
99.07 |
± |
0.22 |
99.28 |
± |
0.19 |
99.17 |
± |
0.21 |
99.17 |
± |
0.21 |
99.22 |
± |
0.20 |
98.04 |
± |
0.32 |
98.04 |
± |
0.32 |
|
22 |
soybean-large |
85.54 |
± |
1.79 |
87.68 |
± |
1.77 |
86.07 |
± |
2.37 |
84.29 |
± |
1.25 |
84.64 |
± |
1.34 |
86.61 |
± |
0.80 |
50.54 |
± |
1.61 |
50.18 |
± |
1.75 |
48.21 |
± |
2.43 |
|
23 |
vehicle |
62.72 |
± |
1.69 |
57.28 |
± |
1.25 |
57.51 |
± |
1.38 |
64.85 |
± |
1.29 |
62.49 |
± |
1.28 |
62.60 |
± |
1.44 |
49.94 |
± |
0.91 |
44.73 |
± |
1.94 |
44.73 |
± |
1.94 |
|
24 |
vote |
94.71 |
± |
0.86 |
90.80 |
± |
1.54 |
91.03 |
± |
1.52 |
94.94 |
± |
0.86 |
95.40 |
± |
0.51 |
95.17 |
± |
0.67 |
95.17 |
± |
0.76 |
95.63 |
± |
0.92 |
95.17 |
± |
0.76 |
|
25 |
waveform-21 |
73.34 |
± |
0.64 |
73.64 |
± |
0.64 |
73.64 |
± |
0.64 |
72.26 |
± |
0.65 |
72.28 |
± |
0.65 |
72.26 |
± |
0.65 |
64.38 |
± |
0.70 |
55.85 |
± |
0.72 |
55.85 |
± |
0.72 |
Top
Gradient based learners have to determine when
to stop climbing. A naive implementation would climb for a fixed pre-set number
of iterations, or would continue climbing as long as the empirical accuracy is
increasing. Our empirical studies (on both ELR and APN) show that these
approaches are problematic, as these systems will typically overfit or underfit.
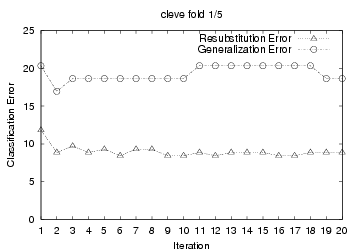
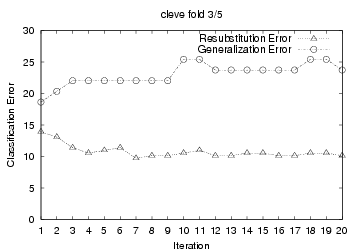
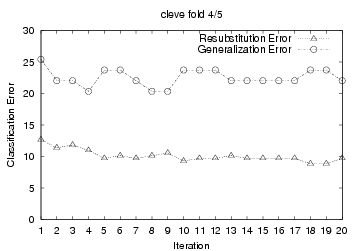
To demonstrate this, we present 5-fold cross
validation learning curves from TAN+ELR training results on the cleve
dataset. For each cross validation run, we used a performed 20 iterations over
the training data; and we plotted the 'Resubstitution Error' and 'Generalization
Error' after each gradient descent iteration (See graphs below.) The
'Generalization Error' is the testing error of the resulting system on the
hold-out fold after each training iteration. (I.e., we divided all cleve
data into 5 fold: {F1, F2, F3, F4, F5}; in each iteration of the first cross
validation run, we used F1+F2+F3+F4 for training, then evaluated the resulting
system against the F5 hold-out testing data to produce the 'Generalization
Error'). Many of the plots show that ELR's gradient ascent
starts overfitting significantly only after
a few training iterations.


Based
on the generalization error plots, we see that ELR should stop after
{2, 1, 1, 4, 5} iterations, for these 5 cross validation
runs. Of course, ELR will not know these "optimal iteration numbers"
as they are based on the hold-out data, which is NOT available at training time.
Fortunately, ELR estimates these
numbers from the available training data, using a standard method we call
"cross-tuning", described on pages 9-10 of the
manuscript, to try to identify the number of climbs (iterations) that is
appropriate for each specific dataset. Cross-tuning first splits the training
set into n parts (folds), then successively trains on n-1 folds
and evaluates on the remaining one. In particular, for each instance, it runs
the ELR algorithm on n-1 folds for a large number of iterations, and
measures the quality of the resulting classifier on the other fold. For each
run, it determines which iteration produces the smallest generalization error.
Cross-tuning then picks the median value m over these runs. Later, when
running on the full dataset (all n folds), it will run for m
iterations before stopping.
The paired t-tests of ELR results on the UCI benchmark
datasets shows that cross-tuning is essential in ELR learning:
- NB+ELR(+xt) <-- NB+ELR(-xt) (p < 0.3) (slightly better),
while
- TAN+ELR(+xt) <-- TAN+ELR(-xt) (p < 0.05) (statistically
better).
(Recall 'x <- y' means 'x is better than y'.)
Here NB+ELR(-xt) is comparable to TAN+ELR(-xt),
whose performance was significantly degraded by overfitting. This shows
cross-tuning can be effective to prevent overfitting especially when learning
parameters of complex BN structures.
The obvious downside of cross-tuning, of course,
is computation expense; see timing
information.
To demonstrate how cross-tuning works to help
avoid overfitting, we revisit the
experiments on the cleve dataset.
For the first cross validation run, we split the training data from folds
{F1,F2, F3, F4} into another 5 folds for cross-tuning; call them 1CT = {1CT1,
1CT2, ..., 1CT5}. (Note: F1 + F2 + F3 + F4 = 1CT1 + 1CT2 + ... + 1CT5.) We then
ran 5 fold cross-tuning on 1CT, here by using 4 folds of 1CT for training and
the remaining 1CT fold for testing, over 20 iterations. Each cross-tuning run
determined an iteration number that produced the smallest testing error on the
hold-out 1CT fold. After 5-fold cross-tuning runs, we took the median value of
the 5 estimates and used it as the iteration number in the training on the full
1CT set.
For this first cross-validation run, this produced an estimate of 2,
which we see (from the "cleve fold 1/5" graph below) is correct. We
similarly computed this quantity for the other four cross-validation scenarios,
producing {2, 1, 1, 3, 5} respectively for the 5 cross validation runs. Notice
cross-tuning identified the correct stopping number in 4 of the 5 cross
validation run. The only exception is the fourth one, where it returned 3, not
4.
Top
classification errors for 20 UCI incomplete datasets
|
classification errors |
NB+EM |
|
NB+APN |
|
NB+ELR |
|
TAN+EM |
|
TAN+APN |
|
TAN+ELR |
|
|
agaricus-lepiota |
4.41 |
0.3 |
4.35 |
0.32 |
0 |
0 |
0.01 |
0.01 |
0 |
0 |
0 |
0 |
|
allbp |
4.22 |
0 |
4.22 |
0 |
3.09 |
0 |
4.12 |
0 |
4.12 |
0 |
3.5 |
0 |
|
allhyper |
2.78 |
0 |
2.78 |
0 |
1.85 |
0 |
2.37 |
0 |
1.85 |
0 |
1.75 |
0 |
|
allrep |
3.5 |
0 |
3.6 |
0 |
3.29 |
0 |
2.47 |
0 |
2.67 |
0 |
2.78 |
0 |
|
anneal |
5.79 |
1.66 |
4.65 |
1.84 |
1.76 |
0.67 |
6.54 |
1.64 |
5.16 |
1.86 |
1.89 |
0.4 |
|
bands |
30 |
1.96 |
29.81 |
1.79 |
25.56 |
1.39 |
25.37 |
2.06 |
24.63 |
2.24 |
26.48 |
2.24 |
|
breast-cancer |
2.59 |
0.84 |
2.59 |
0.84 |
3.74 |
1.14 |
5.18 |
0.89 |
5.76 |
1.27 |
5.04 |
0.85 |
|
cleve |
15.67 |
3.23 |
15.67 |
3.23 |
16 |
2.72 |
18 |
1.62 |
17.33 |
1.63 |
18 |
1.62 |
|
crx |
14.06 |
1.11 |
14.06 |
1.04 |
13.33 |
0.93 |
15.22 |
0.51 |
15.07 |
0.77 |
15.22 |
0.51 |
|
dermatology |
2.19 |
0.82 |
2.19 |
1.11 |
1.92 |
0.7 |
4.66 |
1.11 |
3.29 |
1.11 |
3.29 |
1.27 |
|
dis |
2.11 |
0.56 |
2.11 |
0.6 |
1.39 |
0.26 |
1.71 |
0.27 |
1.57 |
0.3 |
1.43 |
0.22 |
|
horse-colic |
19.73 |
1.66 |
19.73 |
1.66 |
17.81 |
1.15 |
18.08 |
1.01 |
18.36 |
0.82 |
19.73 |
0.93 |
|
hypothyroid |
2.25 |
0.6 |
1.99 |
0.63 |
1.96 |
0.54 |
2.31 |
0.6 |
2.24 |
0.6 |
2.15 |
0.55 |
|
imports-85 |
37.56 |
4.27 |
37.56 |
3.33 |
40 |
2.51 |
34.63 |
1.79 |
34.15 |
3.45 |
33.17 |
3.05 |
|
monk1-corrupt |
36.11 |
0 |
36.11 |
0 |
34.72 |
0 |
22.92 |
0 |
22.22 |
0 |
16.67 |
0 |
|
primary-tumor |
51.64 |
2.69 |
50.15 |
3.01 |
50.45 |
2.89 |
51.94 |
4.51 |
54.93 |
3.38 |
51.94 |
4.51 |
|
sick |
4.71 |
1.21 |
4.89 |
1.36 |
4.11 |
0.77 |
4.46 |
0.85 |
4.46 |
0.88 |
4.18 |
0.71 |
|
sick-euthyroid |
7.03 |
0.93 |
6.96 |
0.89 |
6.36 |
0.99 |
7.25 |
0.89 |
7.15 |
0.91 |
6.46 |
1.1 |
|
soybean-large |
11.97 |
0 |
7.71 |
0 |
8.51 |
0 |
8.78 |
0 |
10.11 |
0 |
10.37 |
0 |
|
water-treatment |
47.31 |
1.91 |
47.31 |
1.91 |
47.31 |
1.91 |
47.31 |
1.91 |
47.31 |
1.91 |
47.31 |
1.91 |
|
average |
15.2815 |
|
14.922 |
|
14.158 |
|
14.1665 |
|
14.119 |
|
13.568 |
|
Paired T-tests ('x <- y' means 'x is better than y'):
NB+ELR <- NB+EM (p < 0.00559)
NB+ELR <- NB+APN (p < 0.026125)
TAN+ELR <- TAN+EM (p < 0.083164)
TAN+ELR <- TAN+APN (p < 0.077631)
|
dataset information * |
instance # |
attribute# |
class# |
|
missing ratio |
missing total/attris |
|
agaricus-lepiota |
8124 |
22 |
2 |
CV5 |
1.39% |
2480/1 |
|
allbp |
2800/972 |
29 |
3 |
train/test |
5.54% |
4556+1508 |
|
allhyper |
2800/972 |
29 |
5 |
train/test |
5.54% |
4556+1508 |
|
allrep |
2800/972 |
29 |
4 |
train/test |
5.54% |
4556+1508 |
|
anneal |
798 |
38 |
6 |
CV5 |
64.94% |
19692/28 |
|
bands |
540 |
29 |
2 |
CV5 |
1.93% |
302 |
|
breast-cancer |
699 |
10 |
2 |
CV5 |
0.23% |
16 |
|
cleve |
303 |
13 |
2 |
CV5 |
0.18% |
7 |
|
crx |
690 |
15 |
2 |
CV5 |
0.65% |
67/7 |
|
dermatology |
366 |
34 |
6 |
CV5 |
0.06% |
8/1 |
|
dis |
2800 |
29 |
2 |
CV5 |
5.61% |
4556 |
|
horse-colic |
368 |
22 |
2 |
CV5 |
23.80% |
1927 |
|
hypothyroid |
3163 |
25 |
2 |
CV5 |
6.74% |
5329 |
|
imports-85 |
205 |
25 |
7 |
CV5 |
1.15% |
59/7 |
|
monk1-corrupt |
288/144 |
6 |
2 |
train/test |
30.17% |
521+261 |
|
primary-tumor |
339 |
17 |
22 |
CV5 |
3.90% |
225/5 |
|
sick |
2800 |
29 |
2 |
CV5 |
5.61% |
4556 |
|
sick-euthyroid |
3163 |
25 |
2 |
CV5 |
6.74% |
5329 |
|
soybean-large |
307/376 |
25 |
2 |
train/test |
4.32% |
705/33 |
|
water-treatment |
523 |
38 |
13 |
CV5 |
2.97% |
591/31 |
* Note all datasets have >200 instances
Top
The page
summarizes all the results on complete data experiments from various papers. In
short, we found that x+ELR performed comparably to C4.5 and SNB.
The following table summarizes our results when comparing ELR vs SVM-light.
(Note that we only ran over the datasets with BINARY class labels.) The
page
presents further details on these SVM experiments.
|
Data set |
NB+ELR |
|
TAN+ELR |
|
GBN+ELR |
|
svm-light c0.05 t1 d2 * |
|
svm-light best value |
|
|
australian |
84.93 |
1.06 |
84.93 |
1.03 |
86.81 |
1.11 |
70.29 |
9.11 |
77.10 |
2.88 |
|
breast |
96.32 |
0.66 |
96.32 |
0.70 |
95.74 |
0.43 |
93.97 |
1.21 |
96.62 |
1.23 |
|
chess |
95.40 |
0.64 |
97.19 |
0.51 |
90.06 |
0.92 |
97.65 |
0.00 |
98.97 |
0.00 |
|
cleve |
81.36 |
2.46 |
81.36 |
1.78 |
82.03 |
1.83 |
72.54 |
4.39 |
80.34 |
3.08 |
|
corral |
86.40 |
3.25 |
100.00 |
0.00 |
100.00 |
0.00 |
96.80 |
5.22 |
100.00 |
0.00 |
|
crx |
86.46 |
1.85 |
86.15 |
1.70 |
85.69 |
1.30 |
70.15 |
8.34 |
70.31 |
6.43 |
|
diabetes |
75.16 |
1.39 |
73.33 |
1.97 |
76.34 |
1.30 |
69.28 |
5.77 |
76.34 |
3.50 |
|
flare |
82.82 |
1.35 |
83.10 |
1.29 |
82.63 |
1.28 |
82.06 |
3.81 |
82.91 |
3.13 |
|
german |
74.60 |
0.58 |
73.50 |
0.84 |
73.70 |
0.68 |
66.20 |
1.75 |
68.70 |
5.75 |
|
glass2 |
81.88 |
3.62 |
80.00 |
3.90 |
78.75 |
3.34 |
79.37 |
8.45 |
79.37 |
8.45 |
|
heart |
78.89 |
4.08 |
78.15 |
3.86 |
78.89 |
4.17 |
76.67 |
2.81 |
83.33 |
3.21 |
|
hepatitis |
86.25 |
5.38 |
85.00 |
5.08 |
90.00 |
4.24 |
86.25 |
5.23 |
86.25 |
5.23 |
|
mofn-3-7-10 |
100.00 |
0.00 |
100.00 |
0.00 |
100.00 |
0.00 |
100.00 |
0.00 |
100.00 |
0.00 |
|
pima |
75.16 |
2.48 |
74.38 |
2.58 |
74.25 |
2.53 |
70.59 |
4.03 |
75.95 |
2.03 |
|
vote |
95.86 |
0.78 |
95.40 |
0.63 |
95.86 |
0.78 |
93.10 |
1.15 |
95.17 |
1.50 |
|
average |
85.43 |
|
85.92 |
|
86.05 |
|
81.66 |
|
84.76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| *
We tried many settings, and found this specific setting, [c=0.05, poly 2
(t=1, d=2)] produced the best average for SVM. (As this is based on ALL
data, this does give svm-light a slight advantage.) |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Paried T-tests ('x <-- y' means 'x is better than y'):
NB+ELR <-- SVM-light[best_ave] (p< 0.023)
TAN+ELR <-- SVM-light[best_ave] (p< 0.036)
GBN+ELR <-- SVM-light[best_ave] (p< 0.0078)
See here
for the 'training time' data for various algorithms.
Top
Finally, our companion paper [GGS97]
also considers learning the parameters of a given structure towards optimizing
performance on a distribution of queries. Our results here differ, as we are
considering a different learning model: [GGS97]
tries to minimize the squared-error score, a variant of Equation 9
that is based on two different types of samples --- one over
tuples, to estimate P(C | E), and the other over queries, to
estimate the probability of seeing each ``What is P(C | E = e)?''
query. By contrast, the current paper tries to minimize classification error
(Equation 3) by seeking the optimal ``conditional likelihood'' score (Equation 4), wrt a single sample of labeled instances. Moreover, our current paper
includes new theoretical results, a different algorithm, and completely new
empirical data.
Recall from the paper,
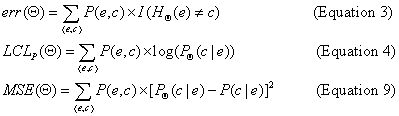
Top
The current paper significantly extends the earlier short papers
- Structural
Extension to Logistic Regression: Discriminant Parameter Learning of Belief
Net Classifiers
Russell Greiner and Wei Zhou
Proceedings of the Eighteenth Annual National
Conference on Artificial Intelligence (AAAI-02), p. 167-173,
Edmonton, Aug 2002.
- Discriminative
Parameter Learning of General Bayesian Network Classifiers
Bin Shen, Xiaoyuan Su, Russell Greiner, Petr Musilek, Corrine Cheng
Proceedings of the Fifteenth IEEE
International Conference on Tools with Artificial Intelligence (ICTAI-03),
Sacramento, Nov 2003.
as it provides
- PROOFS of the claims (Article 1 above simply stated the claims; n.b.,
the proofs are non-trivial)
- many more EXPERIMENTS --
complete series of results on G<T, G~T, G>T
(which is completely new),
for both complete and incomplete data,
comparison not only within different BN structures (NB/TAN/GBN), but also
with other parameter learning algorithms OFE/EM/APN, etc.
- a deeper ANALYSIS of the results.
It also assembles the various pieces into a single coherent story.
Top
For problems or questions regarding this web page, contact
[Bin Shen]
Last updated: 2004/10/11