Nilanjan Ray

Professor
Department of Computing Science
University of Alberta, Canada


Deformable Image Registration

We have utilized neural networks for deformable image registration. In our MIDL 2018 work, we use a neural network to generate deformations required for optimizing SSD (sum of squared difference) cost function used in deformable registration. These are unsupervised or optimization-based methods. Our future endeavor will utilize multi-resolution architectures.

Related Publications
  • A Sheikhjafari, M Noga, K Punithakumar, N Ray, “Unsupervised deformable image registration with fully connected generative neural network," MIDL 2018, Amsterdam. https://openreview.net/forum?id=HkmkmW2jM
  • S. Ghosal and N. Ray, “Deep Deformable Registration: Enhancing Accuracy by Fully Convolutional Neural Net,” Pattern Recognition Letters, vol. 94, pp.81–86, 2017.

Image Sequence Registration


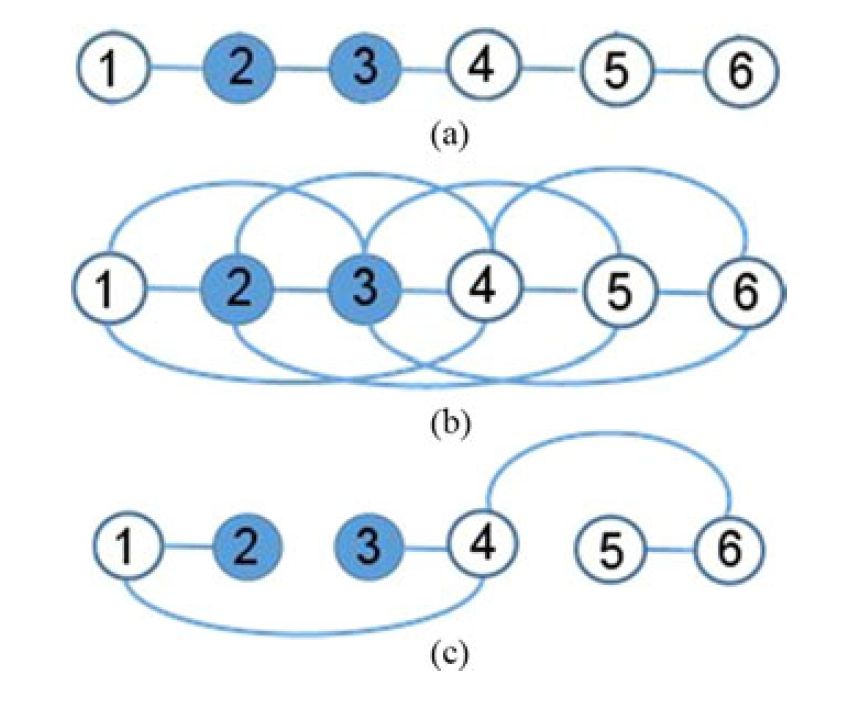
Fig. 1: MST on time sequenced images. (a) Poor quality images are shaded. (b) Local weighted connections. (c) Extracted MST.

Image Sequence Registration with Minimum Spanning Tree

Long sequences of microscopy in-vivo images need to registered. We worked with a minimum spanning tree (MST)-based solution that can (1) automatically select an anchor image, (2) mitigate adverse effects of images with poor quality, (3) work with a very long sequence, and (4) be computationally efficient.

Fig. 2(a) shows a sequence of images, among which two images have poor quality (e.g., defocus). Fig. 2(b) shows a graph with local connections. The edge strength is proportional to sum of squared difference between two images. Fig. 2(c) shows MST extracted from this graph. Note that MST automatically re-orders the images in tree rooted at the 4th image here. Then images in the MST is visited in a breadth or depth first order and are registered to the root (anchor) image.

Related Publications
  • B. Saha, N. Ray, S. McArdle, K Ley, “Selecting the Optimal Sequence for Deformable Registration of Microscopy Image Sequences Using a Two-Stage Minimum Spanning Tree (MST)-based Clustering Algorithm,” MICCAI 2017.
  • B. Saha, N. Ray, S. McArdle, K. Ley, “A Two-stage Minimum Spanning Tree (MST)-based Clustering Algorithm for 2D Deformable Registration of Time Sequenced Images,” IEEE ICIP 2017.
  • N. Ray, S. McArdle, S.T. Acton, K, Ley, “MISTICA: Minimum Spanning Tree-based Coarse Image Alignment for Microscopy Image Sequences,” IEEE Journal of Biomedical and Health Informatics, vol.20, no.6, pp.1575-1584, 2016.
  • S. McArdle, G. Chodaczek, N. Ray, K. Ley, “Intravital live cell triggered imaging system (ILTIS) reveals monocyte patrolling and macrophage migration in atherosclerotic arteries,” Journal of Biomedical Optics, vol.20, no.2, 2015.
  • S. McArdle, ST Acton, K. Ley, N. Ray, “Registering Sequences of In Vivo Microscopy Images for Cell Tracking Using Dynamic Programming and Minimum Spanning Trees,” IEEE ICIP 2014.

Optical Flow


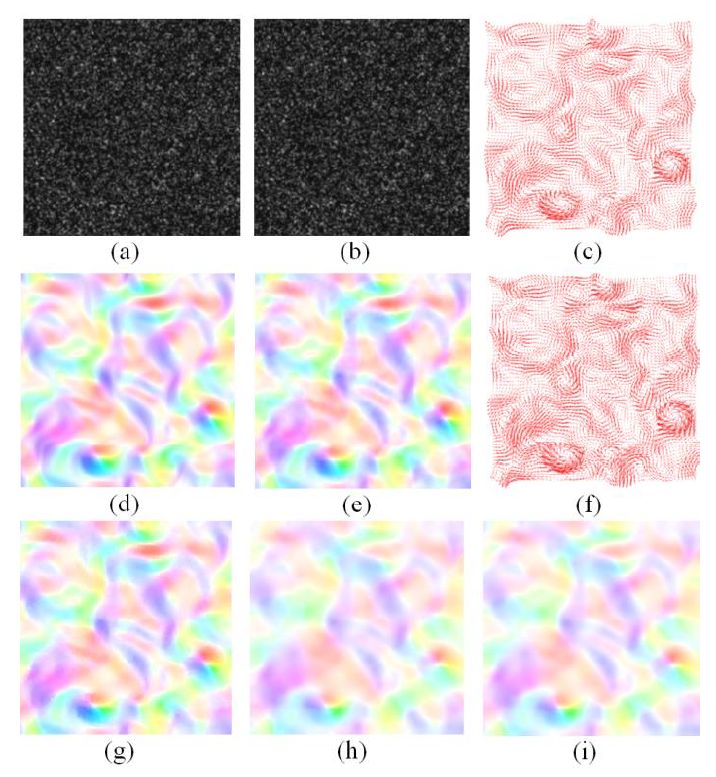
Fig. 2: (a) and (b) a particle image pair; (c) ground truth motion vector; (d) color-coded ground truth motion; (e) Color-coded motion computed by our method; (f) Flow vector computed by our method; (g), (h) and (i) show color-coded motion for three competing methods.

Fluid and Particle Motion Computation by Optical Flow

Fluid motion estimation from time sequenced images is a significant image analysis task. Its application is widespread in experimental fluidics research and many related areas like biomedical engineering and atmospheric sciences. We present a novel flow computation framework to estimate the flow velocity vectors from two consecutive image frames. In an energy minimization-based flow computation, we propose a novel data fidelity term, which (1) can accommodate various measures, such as cross-correlation or sum of absolute or squared differences of pixel intensities between image patches, (2) has a global mechanism to control the adverse effect of outliers arising out of motion discontinuities, proximity of image borders, and (3) can go hand-in-hand with various spatial smoothness terms. Further the proposed data term and related regularization schemes are both applicable to dense and sparse flow vector estimations. We validate these claims by numerical experiments on benchmark flow data sets.

Related Publication
  • N. Ray, “Computation of fluid and particle motion from time sequenced image pair: a global outlier identification approach,” IEEE Transactions on Image Processing, vol.20, no.10, pp.2925-2936, 2011.