Experiments

The experimental design used to test Loki-2's simulation-based performance is the same as described in Section 4.3.1. In a tournament, there are eight Loki-1 players playing against two Loki-2 players. A tournament consists of 2,500 different deals played ten times each (i.e. 25,000 games). The number of trials per simulation was chosen to meet real-time constraints and statistical significance. In the experiments, 500 trials per simulation were performed, since the results obtained after 500 trials were quite stable. For example, 4.6% of the betting actions selected with 100 trials changed after more trials were performed, whereas only 0.5% of the decisions were changed after 500 trials.

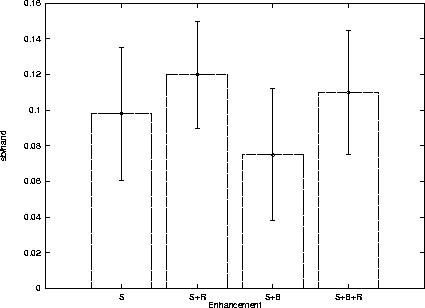
Selective sampling simulation was tested alone and in combination with the PT enhancements. Figure 5.2 shows the increment in Loki-2's performance in a homogeneous environment obtained by using the following modifications in Loki-1:

• S = Selective sampling simulation,
• S+R = Selective sampling simulation with PT-based reweighting,
• S+B = Selective sampling simulation with PT-based betting strategy as the action generation mechanism inside the simulation, and
• S+B+R = Selective sampling simulation with PT-based reweighting and PT-based betting strategy.

  

Figure 5.2: Selective sampling simulation experiments

In the graph, Loki-1's performance is the baseline for comparison. Selective sampling simulation (S) represents an improvement of $0.098 \pm 0.038$ small bets per hand (sb/hand). By adding both PT enhancements (S+B+R), an improvement of $0.11 \pm 0.035$ is obtained. As can be seen in the graph, the effects of S, B and R are not additive. These enhancements may exploit the same aspect of the opponents' play and their effects overlap. Another reason may be the hyper-aggressive playing style of the simulation-based players. They are very successful against Loki-1 players, and can lead to over-optimistic conclusions about the performance improvement represented by S. Since the B enhancement allows us to simulate less tight opponents, S+B may result in a less aggressive playing style, lowering S+B winnings against Loki-1 opponents.

Also, one has to consider that the larger the winning margin, the smaller the opportunity there is for demonstrating further improvement against the same opposition. There is a limit to how much money one can make from an opponent in a game. Two other experiments were carried out raising the baseline for comparison. In the first experiment, two Loki-2s with S were matched with a field of Loki-2s with B+R. The S enhancement won $0.023 \pm 0.044$ sb/hand. In the second experiment, the same field of opponents (B+R) played against two Loki-2s with S+B+R. The S+B+R's winning rate was $0.087 \pm 0.038$ sb/hand.

A mixed environment experiment was conducted to see how well selective sampling simulation performed against different playing styles. In this experiment, the field of opponents was composed of pairs of players with the styles: tight/aggressive (T/A), loose/passive (L/P) and loose/aggressive (L/A), as well as two pairs of tight/passive (T/P) players. From each pair of players, one player used selective sampling simulation and the other one was a Loki-1 player. Figure 5.3 shows the average performance of the players without simulation (AVE) and the average performance with simulation (AVE+S). The average improvement obtained for all different players by using simulation is 0.036 sb/hand.

  

Figure 5.3: Selective sampling simulation - mixed environment

  

Figure 5.4: Loki-2's behaviour on IRC

Loki-2's playing ability with the three enhancements (S+B+R) was also tested against human opposition in on-line poker games on the Internet Relay Chat (IRC). Loki-2's winning rate is 0.13 sb/hand in 26217 games (Loki-1's winning rate on IRC was 0.08 sb/hand). Figure 5.4 shows Loki-2's behaviour on the first level of IRC.