References
Upright, C., Cobzas, D., Jagersand, M.
Smooth and non-smooth wavelet basis for capturing and representing light
,
International Symposium on 3D Data Processing, Visualization and Transmission (3DPVT) 2008
Upright, C., Cobzas, D., Jagersand, M.
Wavelet-based Light Reconstruction from a Single Image,
Canadian Conference on Computer and Robot Vision (CRV) 2007
|
Description
Indirectly estimating light sources from scene images and modeling the light distribution is an important, but difficult problem in computer vision. A practical solution is of value both as input to other computer vision algorithms and in graphics rendering. For instance, photometric stereo and shape from shading requires known light. With estimated light such techniques could be applied in everyday environments, outside of controlled lab conditions. Light estimated from images is also helpful in augmented reality in order to consistently relight an artificially introduced object.

Example of light basis (top) and the scene illuminated with the light basis (bottom). From left to right: Haar, Daubechies, first order spherical harmonic.
While algorithms that recover light as individual point light sources work for simple illumination environments, it has been shown that a basis representation achieves better results for complex illumination.
We propose a novel light representation based on a wavelet basis. We experimented with both smooth (Daubechies) and non-smooth (Haar) basis. The new wavelet representation is able to efficiently represent both diffuse and sharp light effects as a consequence of the wavelet property of providing local support in both spatial domain (here image dimension) and frequency domain.
We consider the problem of estimating light from cast shadows and specular highlights in images. We assume that the geometry is known for part of the scene. In everyday images, one can often obtain a CAD model of man-made objects (e.g. a car), but the rest of the scene is unknown.


Results of the light reconstruction method. Comparison between 4 light basis (Haar, Daubechies, Discrete hemisphere and Spherical harmonics). (top) original lightmaps (bottom) reconstructed lightmaps.
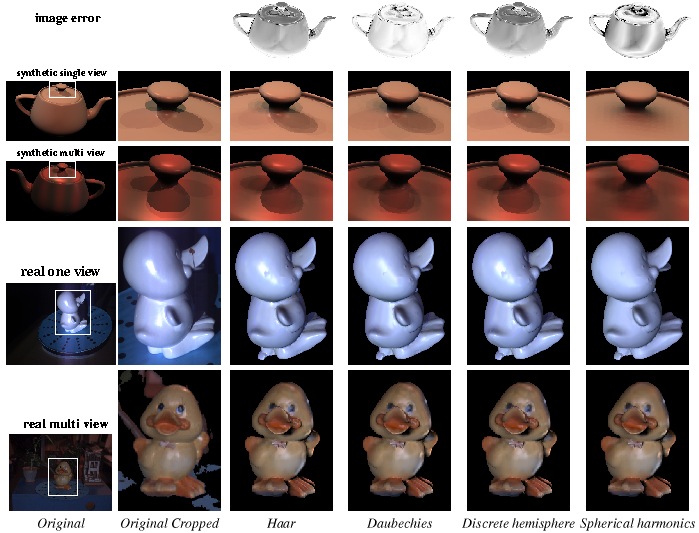
Different scenes rendered with the recovered light. Comparison with original images.
|



