 |
AIxploratorium
|
 |
|
|
||
Use a Decision Tree to determine who should win the gameGive up?
We first need to present some notation: We view this predictor as a "classifier", as it is classifying this future game into either the "Won" or the "Lost" class. We will also view each game description, such as [Where=Away, When=9pm, FredStarts=No, JoeOffense=Center, JoeDefense=Forward, OppC=Tall].as an instance, composed of a set of Attribute=Value assignments (eg, Where is an attribute, and Away is its associated value). (Note this also corresponds to a database record.) As we did not indicate the outcome of this game we call this an "unlabeled instance"; the goal of a classifier is finding the class label for such unlabeled instances. An instance that also includes the outcome is called a "labeled instance" --- eg, the first row of the table
corresponds to the labeled instance [Where=Home, When=7pm, FredStarts=Yes, JoeOffense=Center, JoeDefense=Forward, OppC=Tall, Outcome=Won]. Decision TreesIn general, a decision tree is a tree structure; see left-hard figure below.
Like biological trees, our Computer Science trees also have a single root, whose branches lead to various subtrees, which themselves may have have sub-subtrees, until terminating in leaves. A computer science tree, however, grows upside-down: its root is at the top, and its branches go down. Go figure. Technically: a tree is a set of nodes and arcs, where each arc "descends" from a node to the children of that node; in the figure above, the "FredStarts" node has 2 arcs: one going to the left-most "Won" node (via the "Yes"-arc), and another going (via the "No"-arc) to the "JoeOffense" node. That "JoeOffense" node is itself the root of a subtree, as it has children "Won" and "Lost". Nodes that are not leaves -- both the root "FredStarts", as well as "JoeOffense" --- are called internal nodes Again, see Notation for more details.) Note each unlabeled instance (remember "instance" -- see above) corresponds to a path through the tree, from the root to a leaf: eg, the instance representing the upcoming MallRat/Chinook game will go "right" at the root, as Fantastic Fred is not starting, then go left at the JoeOffense node, as Joe is playing center on offence. This will end on the "Won" leaf node. That is, this tree is asserting its guess that the MallRats will win this game. Of course, this is just the opinion of this single tree. Note the data has a different opinion: there are 4 previous games where "Fred did NOT start and Joe played Center on offense", and the MallRats won only 2 of these 4 ! Similarly, the "FredStarts = Yes" branch points to a "Lost" node; note however the MallRats actually WON 8 of 10 games where Fred started. This information clearly lessens our confidence that this specific tree is correct, as we naturally assume that these previous games should be relevant. Our task, then, is: How to use a data set (such as the records from the previous games) to LEARN an accurate decision tree? We will then use that learned tree to "classify" a new example: here, to determine whether the MallRats will win this upcoming game; see figure below.
Learning Decision TreesA decision tree needs to decide when to split on which attributes. In particular, what is the appropriate root (ie, top-most) attribute? Should it be "FredStarts" or "JoeOffense" or "Where" or ... ? It is then clear which records (ie, previous games) go to which child: eg, if the root was "FredStart", the records for all 10 "FredStart" games go left (following the "Yes" arc)
and the other 10 "Fred didn't start" games all go right. Another question is "When to stop?". For example, after following the "FredStarts = Yes" arc from the root, we could stop here. Note, however, that the MallRats won 8 of these 10 games, and lost the remaining 2. While this does suggest the MallRats will win in this situation, there are counter-examples, which suggests we should ask some other question here. Here, if we ask "Where", we see that the MallRats won all 6 of the Where=Home games that Fred started; see below:
On this branch, we can confidently stop, and produce a "Won" label; see tree. The idea here is to continue splitting until "purity" -- ie, until all of the records that reach the node have the same label. We then create a leaf node, whose value is that label (here, "Won"). Actual Demo
Why not just chose attributes randomly? To find out...
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
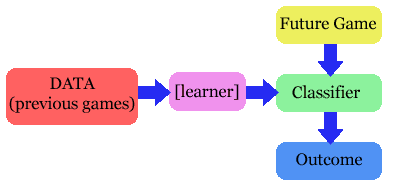
Below we present a way to learn a good "predictor",
which we can then use to predict whether the MallRats will win any specified
game... and in particular, to predict who will win this MallRat/Chinook game.
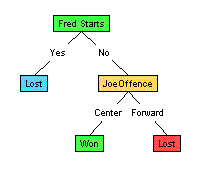
So, for now, the only issue is deciding which attribute to test.
How?