histogram of orientation

 

  

Rotation Invariant Local Frequency Descriptors for Texture Classification

This goal of this project is to develop a novel rotation invariant method for texture claqssification based on local frequency components. The local frequency components are computed by applying 1D Fourier transform on a neighboring function defined on a circle of radius R at each pixel. Three sets of descriptor are extracted from the low frequency components, two based on the phase and one based on the magnitude. The proposed descriptors are rotation invariant and very robust to noise. The combination of these three sets are used for texture classification. The experimental results show that the proposed
method outperforms state-of-the-art methods in the Brodatz, Outex, and CUReT datasets. Moreover, the descriptors are very robust especially in presence of high levels of noise.

Reference

R. Maani, S. Kalra, and Y.H. Yang, "Rotation Invariant Local Frequency Descriptors for Texture Classification," IEEE Trans. on Image Processing, Vol. 22, No. 6, 2013, pp. 2409-2419.

 

LFD

  

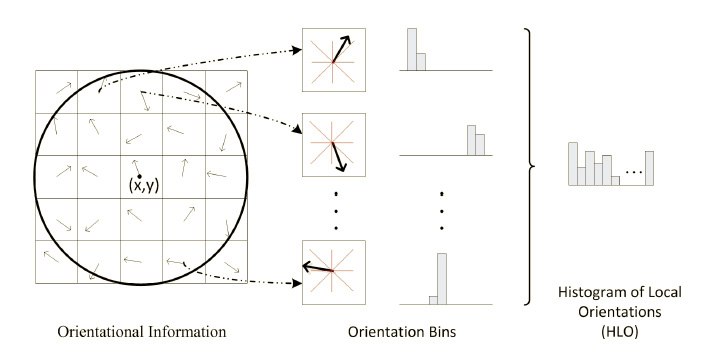
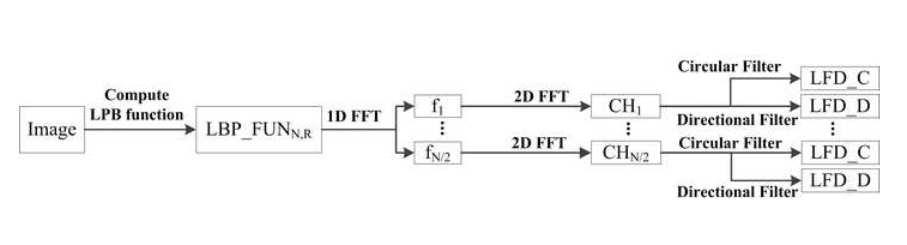
Noise Robust Rotation Invariant Features for Texture Classification

This project presents a novel, simple, yet powerful and robust method for rotation invariant texture classification. Like the Local Binary Patterns (LBP), the proposed method considers at each pixel a neighboring function defined on a circle of radius R. We define local frequency components as the magnitude of the coefficients of the 1D Fourier transform of the neighboring function. By applying different bandpass filters on the 2D Fourier transform of the local frequency components, we define our Local Frequency Descriptors (LFD). The LFD features are added dynamically from low frequencies to high. The features defined in this paper are invariant to rotation. As well, they are robust to noise. The experimental results on the Outex, CUReT, and KTH-TIPS datasets show that the proposed method outperforms state-of-the-art texture analysis methods. The results also show that the proposed method is very robust to noise.

Reference

R. Maani, S. Kalra, and Y.H. Yang, "Noise Robust Rotation Invariant Features for Texture Classification," Pattern Recognition, Vol. 46, Issue 8, 2013, pp. 2103-2116. (http://dx.doi.org/10.1016/j.patcog.2013.01.014).

 

symmetric neighborhood

A symmetric neighborhood structures.

 

Similarity Measure and Learning with Gray Level Aura Matrices (GLAM) for Texture Image Retrieval

In this project, we develop a new similarity measure for texture images based on the gray level aura matrices (GLAM), originally proposed by Elfadel and Picard for modeling textures. With the new similarity measure, a support vector machine (SVM) is used to learn pattern similarities for texture image retrieval. In our approach, a texture image is first segmented into clusters of gray
level sets. Defined based on the aura measures, a normalized aura matrix is calculated between the gray level sets of the image. The similarity between two texture images computed by the distance of their corresponding normalized aura matrices is defined as the aura matrix distance. The smaller the distance, the more similar are the two textures. To enable the learning of similarity for texture image retrieval, an existing SVM method is adapted to our application, but with a different similarity measure function, different texture feature vectors, and a different similarity ranking scheme for the final retrieved images based on the GLAM. We compare our approach experimentally with existing approaches by performing texture image retrieval from the Brodatz database and the Vistex database. The experimental results show that the proposed approach has performance significantly better than existing approaches with an average successful retrieval rate of 99% - 100% vs 89% - 92% using other approaches.

Reference

X. Qin and Y.H. Yang, "Similarity measure and learning with gray level Aura matrices (GLAM) for texture image retrieval," Proc. IEEE CVPR, 2004, pp. 326-333. (http://dx.doi.org/10.1109/CVPR.2004.1315050)