Extra material from class, usually done on the whiteboard.
Contents:
The sum game played by economic rules in class, part 2:
More details in the spreadsheet that I shared
Day 2:
How to play out the integers: Continue the game after move 8 above.
The sum game played by economic rules in class, so far:
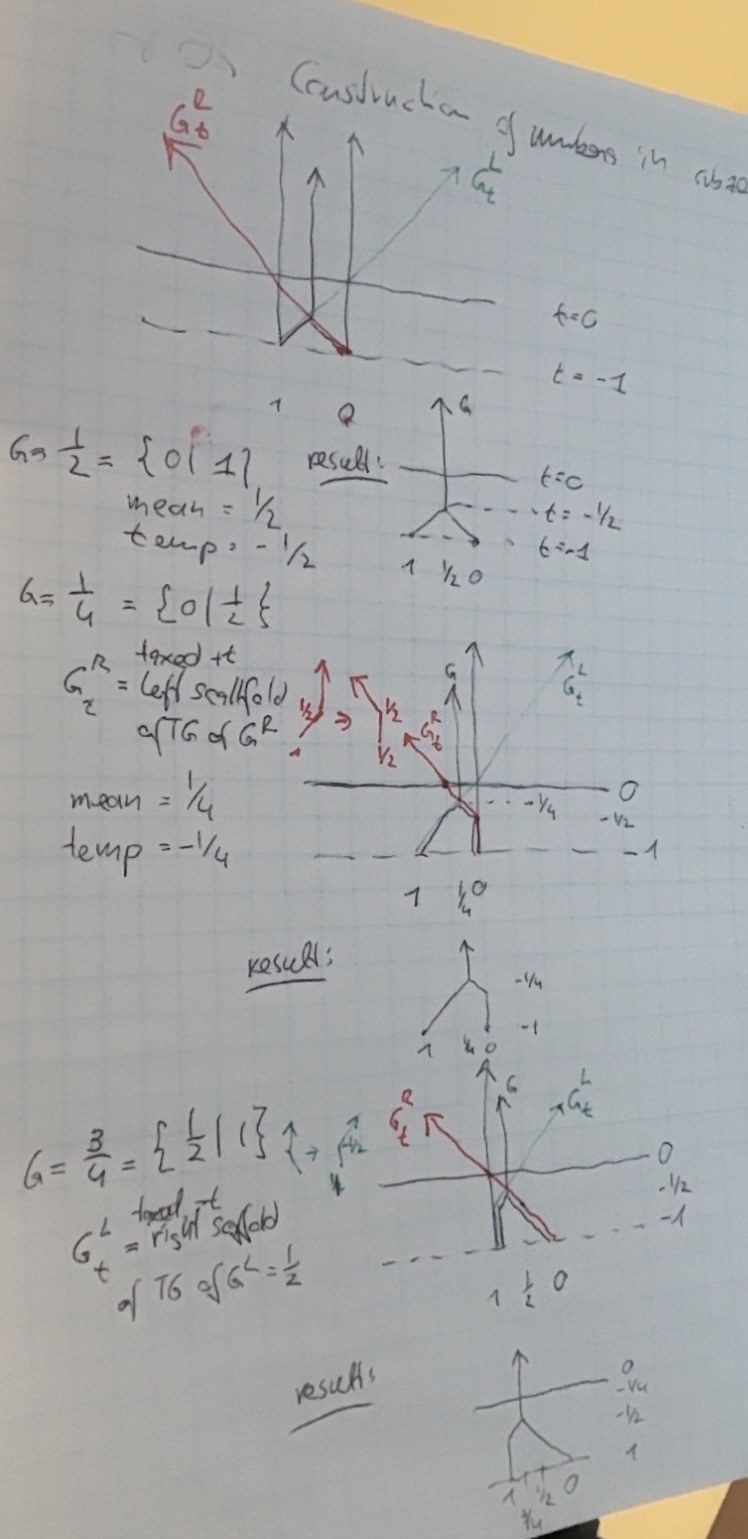
Constructing the thermographs of numbers 1/2, 1/4, 3/4 in subzero thermography.
Note: taxed left options in green, I did not have a blue pen handy...
G.Cool(t) applies a tax of t to game G, giving Gt
{6|-6}.Cool(3)
{6|-6}.Cool(1/2)
{6|-6}.Cool(-1/2)
{6|-6}.Cool(-1) // CGSuite does not like this...
Examples from slides, experiments with cooling them
4.Cool(1) // nothing happens to integers
(1/2).Cool(1/8) // nothing happens to fractions
// t(4|-4) = 4
{4|-4}.Cool(1)
{4|-4}.Cool(2)
{4|-4}.Cool(4)
{4|-4}.Cool(5)
//t(4|{−4|−10}) = 11/2
{4||-4|-10}.Cool(3)
{4||-4|-10}.Cool(5)
{4||-4|-10}.Cool(11/2)
{4||-4|-10}.Cool(6)
{4||-4|-10}.Cool(1000)
//t(4|{−4|−20}) = 8
{4||-4|-20}.Cool(6)
{4||-4|-20}.Cool(8)
//t(4|{−4|−100}) = 8
{4||-4|-100}.Cool(8)
Most thermographs have a simple structure, just a few line segments plus a mast. However, you can create thermographs with arbitrary many line segments.
G := {2|-2} + {4|-4} + {6|-6} + {8|-8} + {10|-10} + {12|-12} + {14|-14}
G.Thermograph.Plot()
(G+G.Cool(1)).Thermograph.Plot()
H := {16|-16} + {18|-18} + {20|-20} + {22|-22} + {24|-24}
H.Thermograph.Plot()
(G+H).Thermograph.Plot()
// next one is a bit slow
(G+G.Cool(1) + H).Thermograph.Plot()
// next one took forever and I killed it with Menu-System-Kill calculation.
// It is the TG of the sum of all switches from +-1 to +- 24
(G+G.Cool(1) + H +H.Cool(1)).Thermograph.Plot()
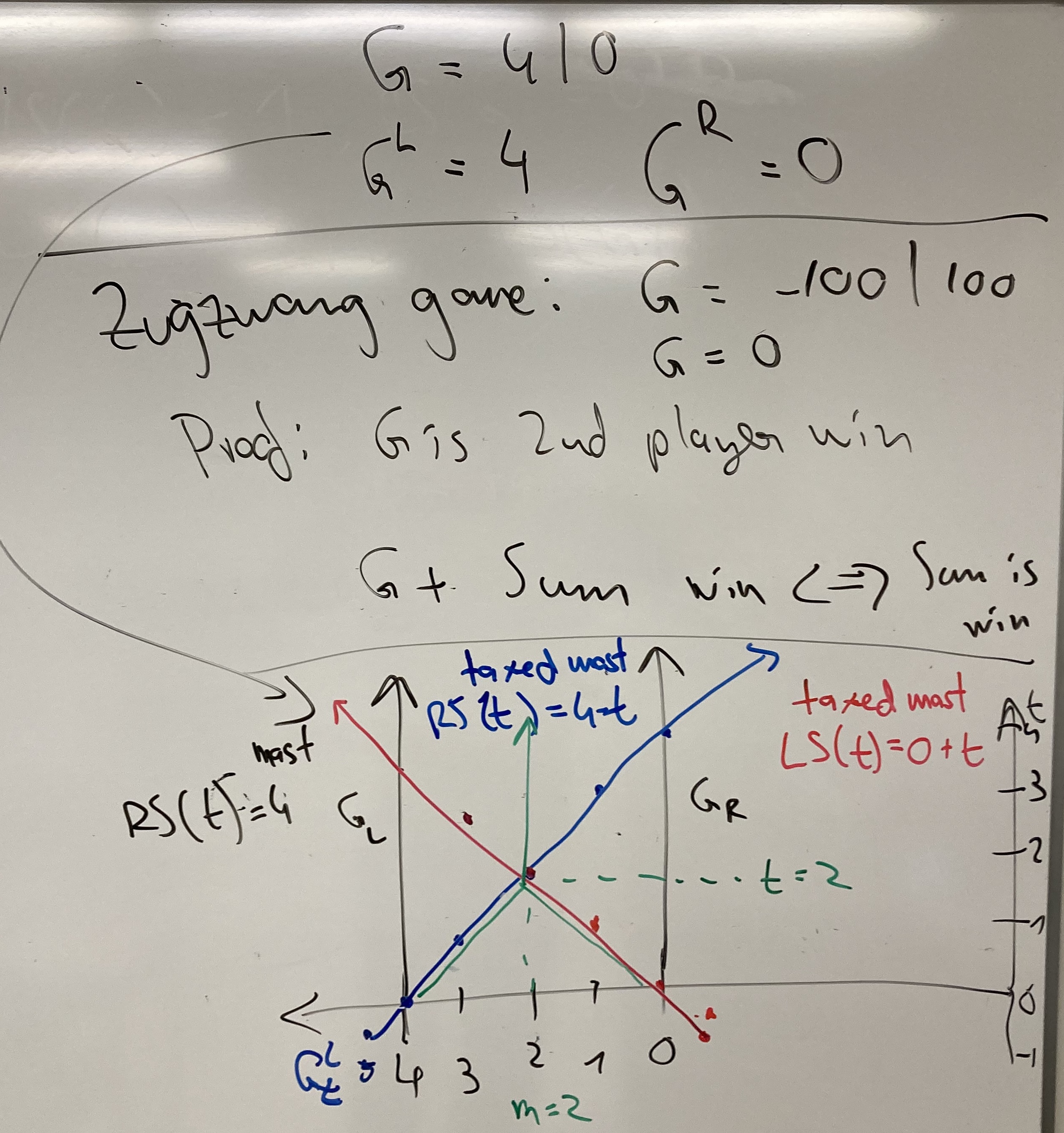
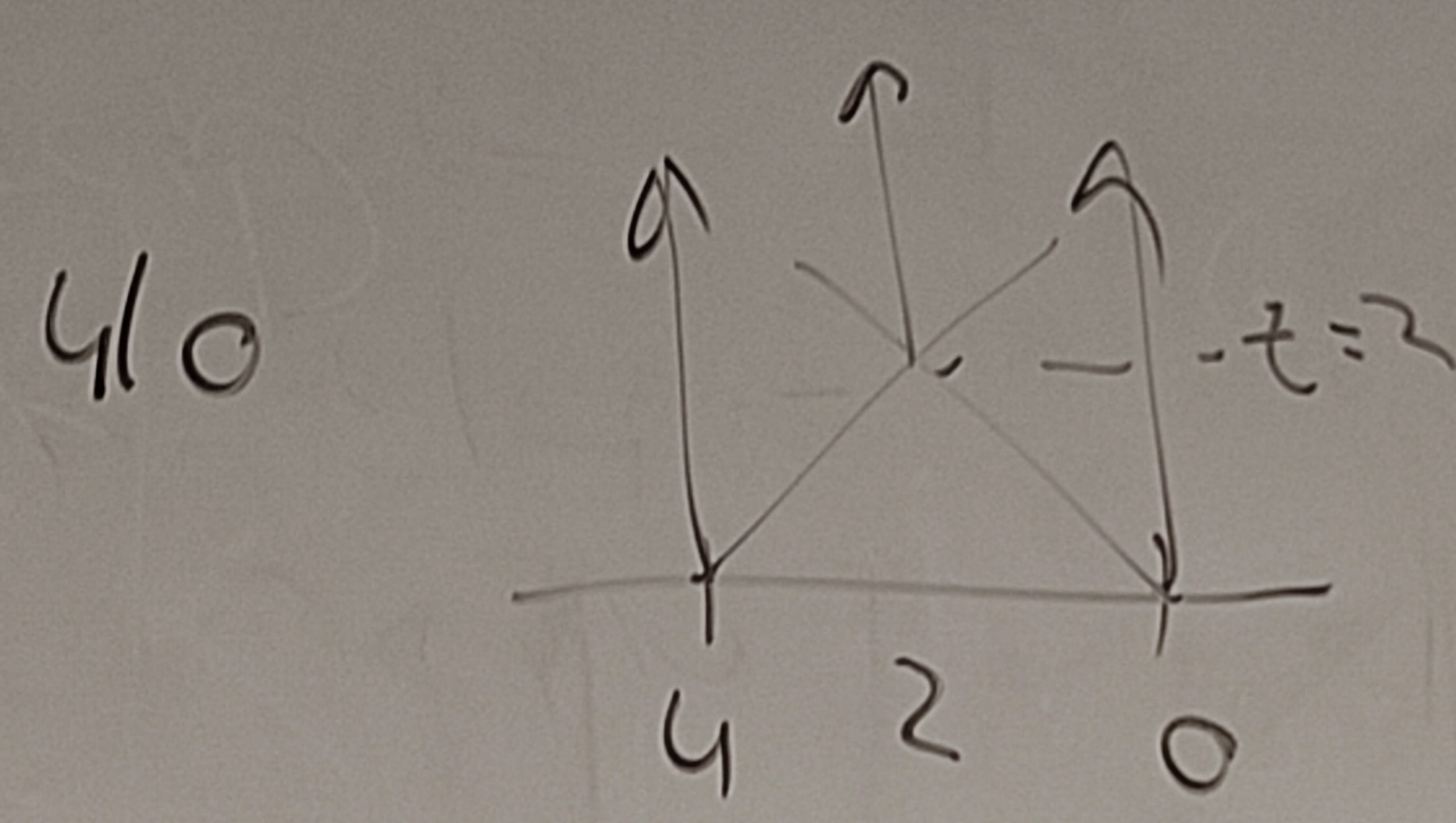
Thermograph of gote situation G = 4|0. Mean(G) = 2, temperature(G) = 2
In CGSuite: Explorer({4|0}), then click on Selection.CanonicalForm.Thermograph.Plot() in the drop down list in the bottom left, where it says "Select or enter...". CGSuite shows only the final result, not the construction steps.
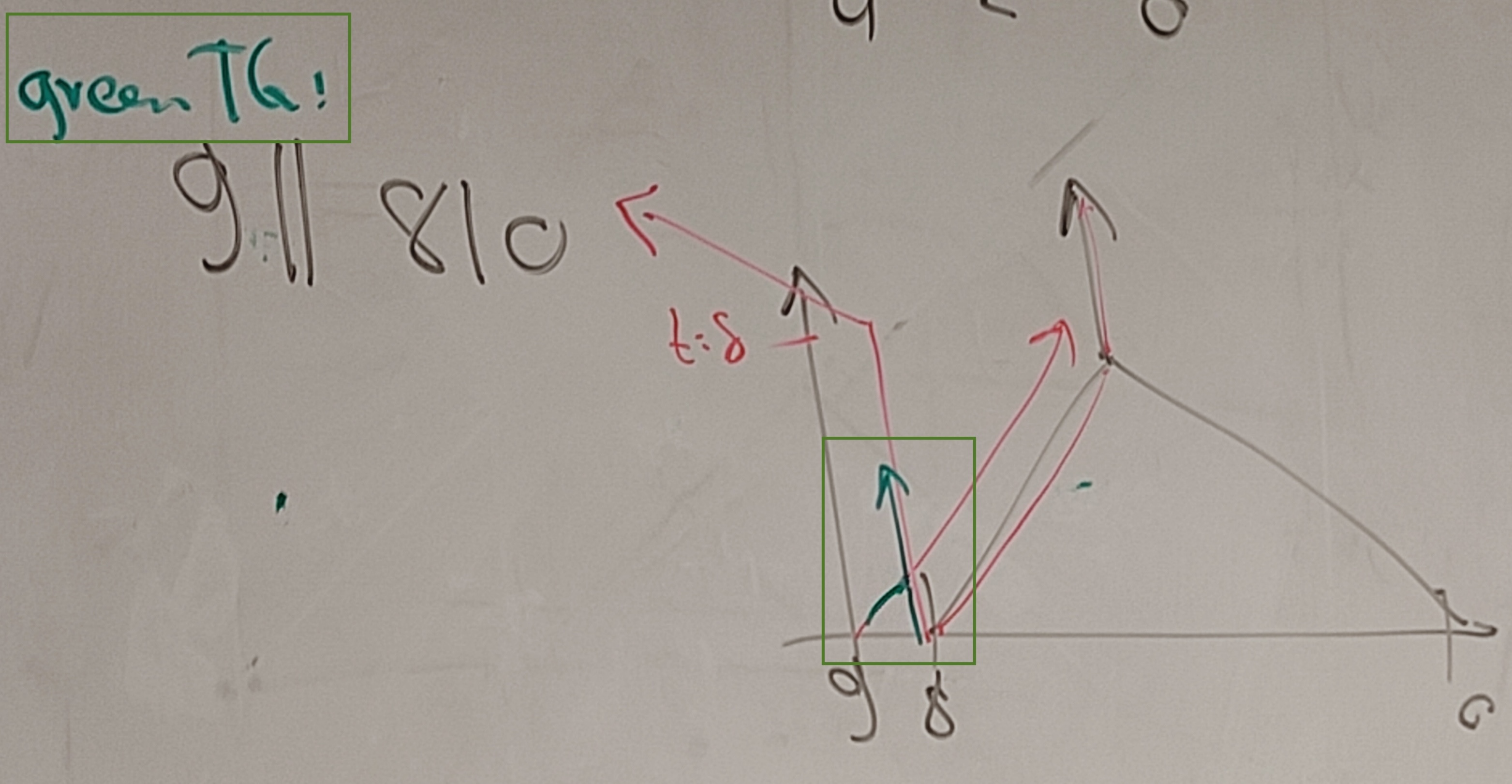
Thermograph of one-sided sente G = 9||8|0. Mean(G) = 8, temperature(G) = 1.
Explorer({9||8|0})
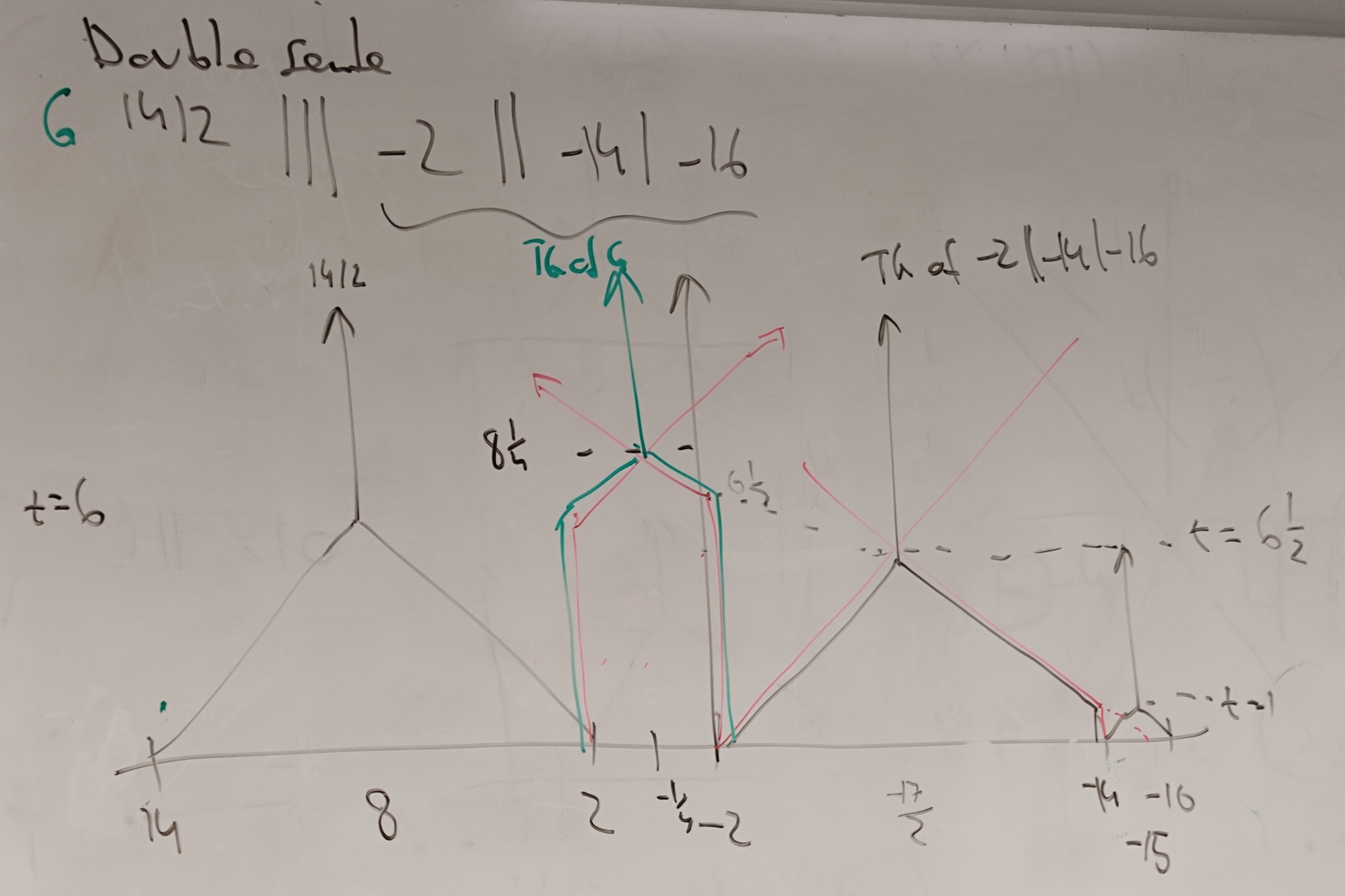
Thermograph of double sente G = 14 | 2 ||| -2 || -14 | -16. Mean(G) = -1/4, temperature(G) = 33/4 = 8 1/4.
Explorer({14|2|||-2||-14|-16})
In CGSuite, you can click on the node (circle) in the top right,
select "Expand sensible lines", then click on other nodes to see e.g.
the thermographs of 14|2 and -2||-14|-16 that were used
in the construction.

Thermograph of 1 || -2|-4.
Explorer({1||-2|-4})
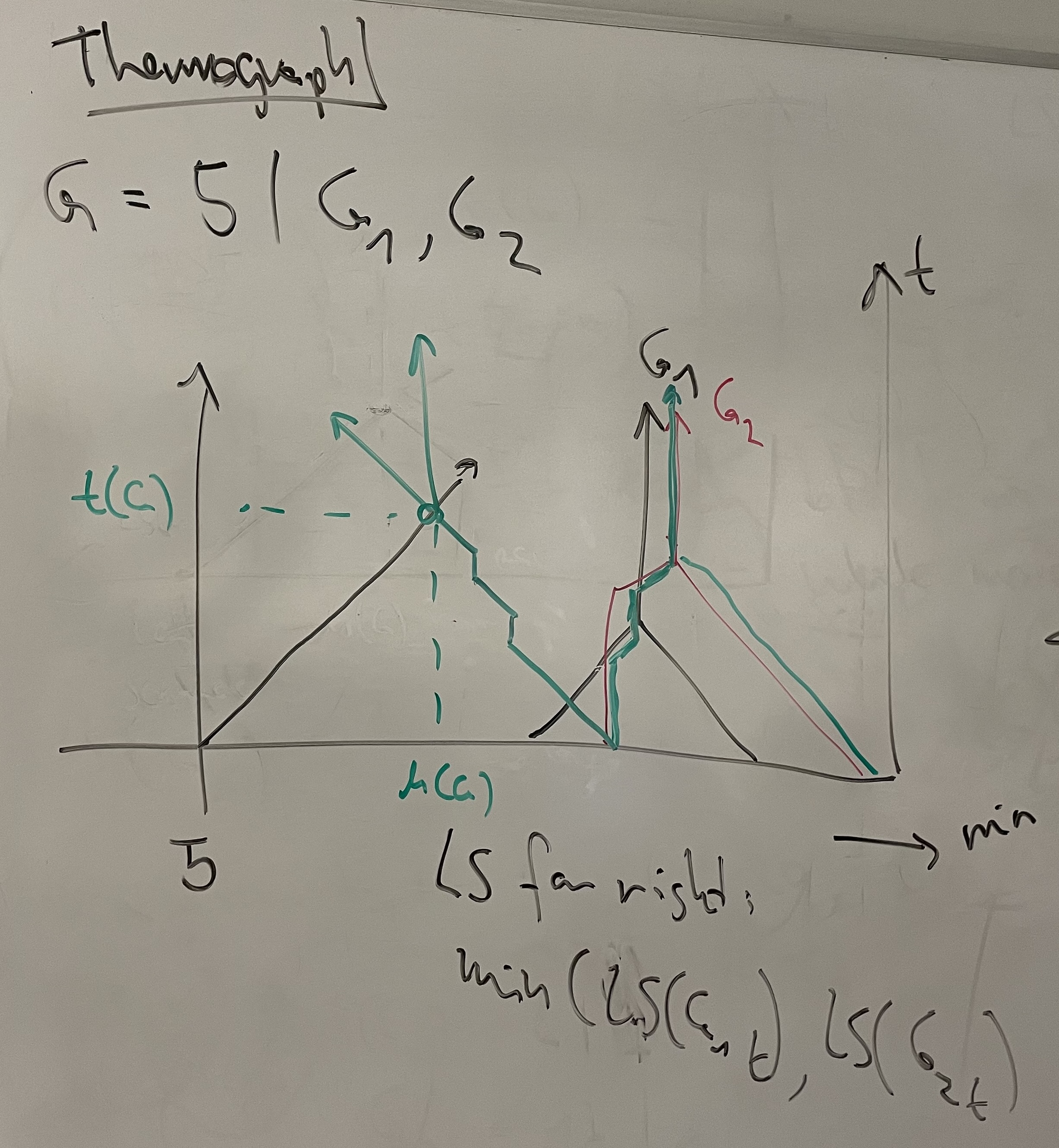
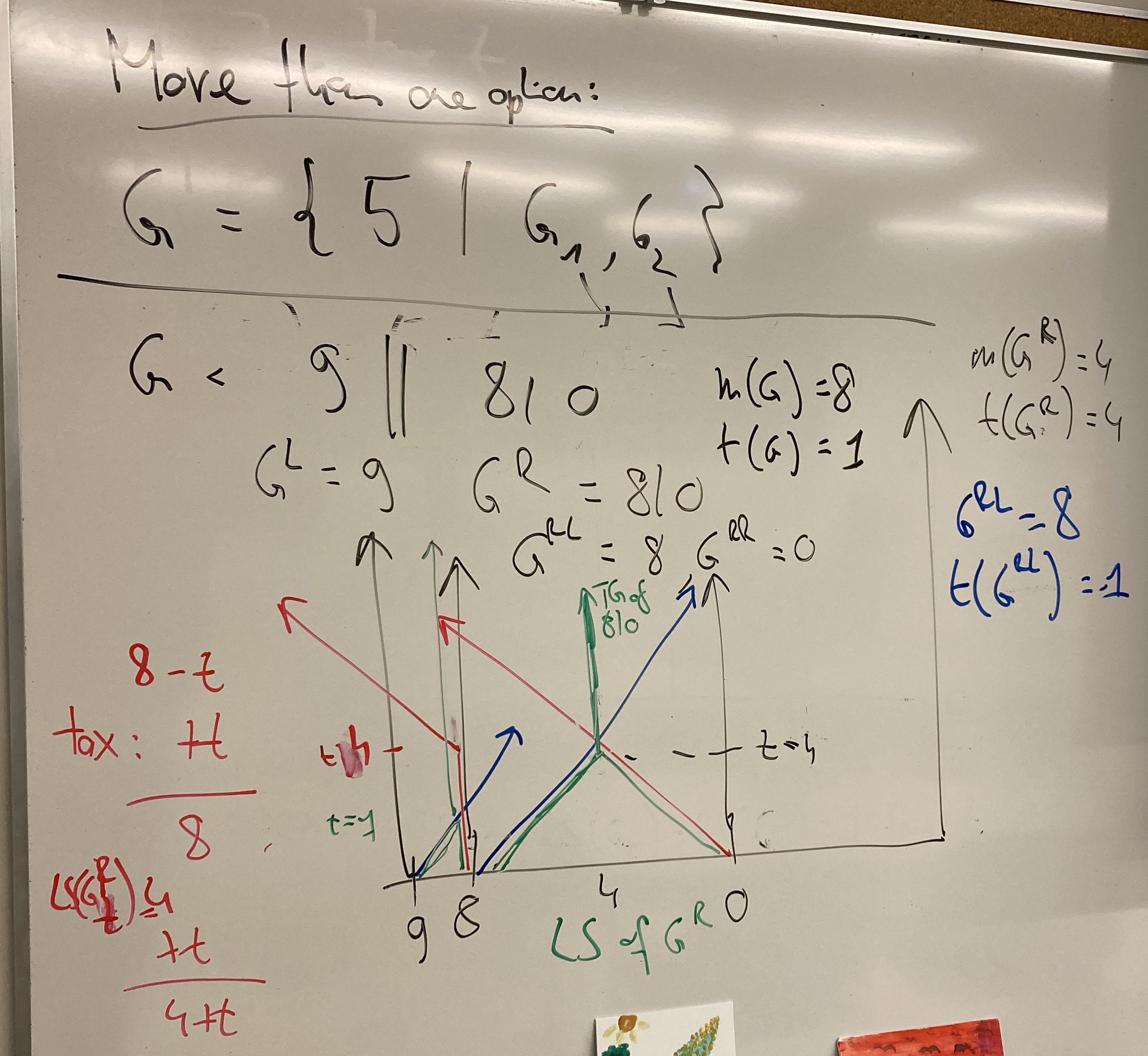
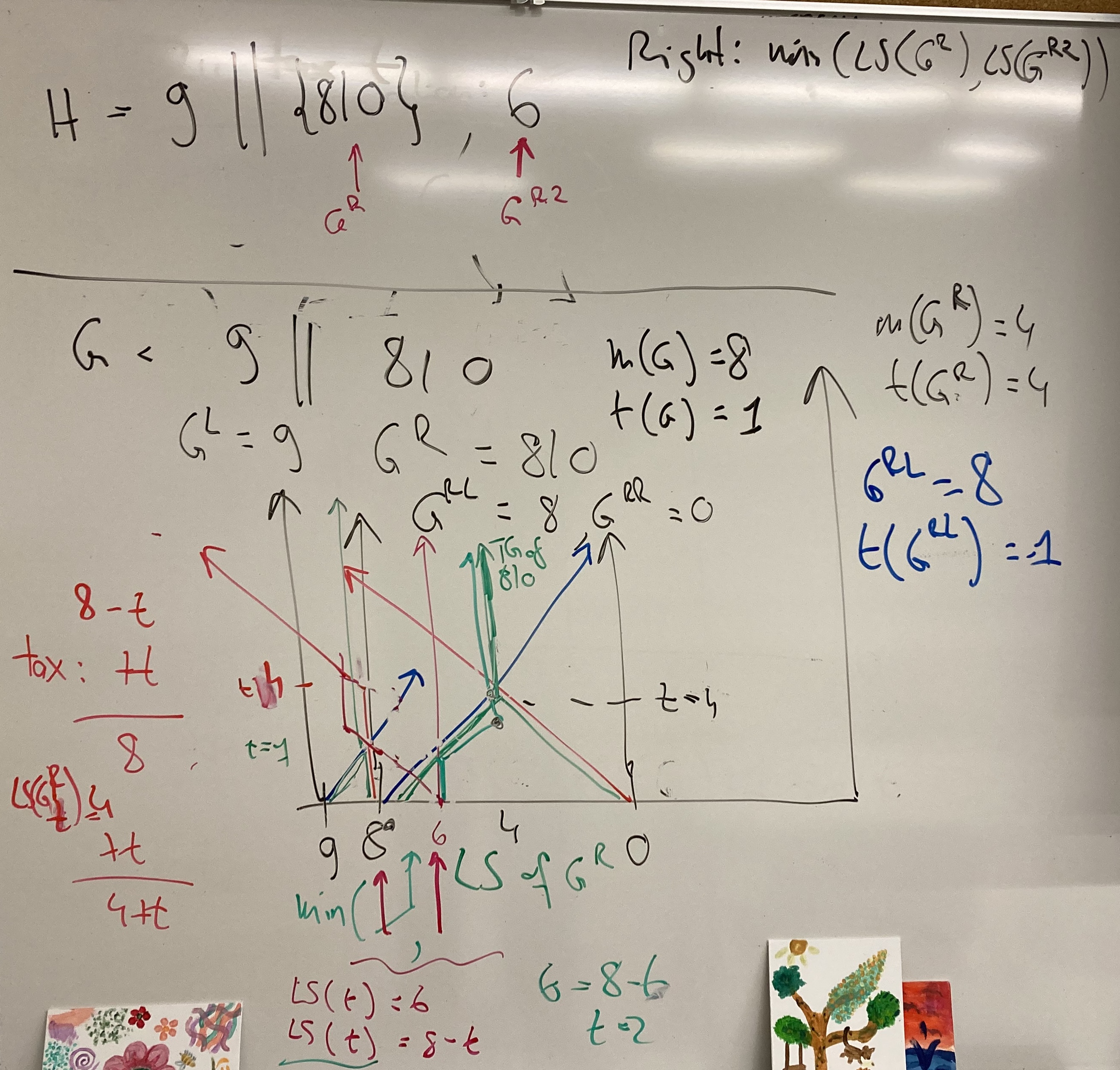
Thermograph construction with two right options, G = 5 | G1, G2. LS for right: min(LS(G1_t), LS(G2_t)). The games G1 and G2 are such that at some temperatures, a move to G1 is better, and at other temperatures, a move to G2 is better. In the figure, the thermograph for G1 is in black, and G2 in red. At each t, the min of the two LS is shown in green. It follows red at low temperatures, then black, then red again. The min RS in this example is always from G2, and is also shown in green. But thi
I wrote these notes in response to one student. I am sharing them here since they may be of more general interest.
There is a survey article Scoring games: the state of play by Urban Larsson, Richard J. Nowakowski and Carlos Pereira Dos Santos, in Games of No Chance 5. Personally, I know very little about the subject even though it started with Go...but I would be happy if you did such a project.
For full-board (single) games there is a lot of work, and almost all the more recent (15-20 years) papers use ML in some form. E.g. the policy function in AlphaGo etc., and many hand-made but computer-tuned heuristics before that. Also many statistics-based schemes.
There are also a few game-independent move ordering heuristics such as history heuristic for such games. A very basic kind of "learning".
Iterative deepening search and using the best move from the previous iteration is the standard move ordering in alphabeta. In MCGS, we do not have any numeric evaluation, only win-loss-unknown.
For neural networks for speeding up proofs, there is the work on Proof Cost Networks (PCN) by the group in Taiwan that we work with: AlphaZero-based Proof Cost Network to Aid Game Solving. Ti-Rong Wu, Chung-Chin Shih, Ting Han Wei, Meng-Yu Tsai, Wei-Yuan Hsu, I-Chen Wu.
poster
paper
I do not know if and how it can be adapted to sums, but it would be interesting to think about.
For combinatorial (sum) games in general I do not know too much about move ordering. It would be nice to have something general for MCGS, but where to start? The papers by our group (Taylor for Clobber and Henry Du for NoGo) talk about some move ordering strategies for specific games, such as play in the middle to split games early into smaller subgames.
There are at least two levels to this question for sums - 1. which subgame to play in, and 2. which move to play there.
My old paper with Zhichao Li Locally Informed Global Search... (on our reading list) shows that temperature is a super-strong heuristic for move ordering in search. The games in that paper have only one move in each subgame. We have some unpublished experiments with multiple moves per subgame, but the complexity of solving grows much more quickly.
My even older PhD thesis uses incentives for solving Go endgame puzzles, but mostly for the case where you do not need any global search. The are many cases where there is some (or even much) ordering between moves but it is not perfect, and we still need search. My PhD thesis used a very naive approach for that case. I worked on a better algorithm for Go about 3-4 years ago. It works, but it is embedded in a very old Go program, so hard to work with. A clean implementation of such algorithms, e.g. in MCGS, would be a good project.
Regarding ML and game rules, I do not see how to learn directly from rules, but I can see e.g. learning from sampling of (local? global?) game trees. There is a huge literature on "General Game Playing" where they try such things (again, not for the case of sum games afaik)
Note: LeftStop and RightStop are what we called LeftScore and RightScore.
Sums-Incentives:
Slide 3:
A := {1|-1}; B := {2|-2}; C := {3|-3}; D := {4|-4}
A.LeftIncentives // a set
A.LeftIncentives.Head // first element in set
D.LeftIncentives.Head >= A.LeftIncentives.Head // check dominated incentive
D.LeftIncentives.Head >= B.LeftIncentives.Head
D.LeftIncentives.Head >= C.LeftIncentives.Head
// these three together prove that D is the dominating incentive.
// Note that I only test the Head of a set since these sets only have
// one element. A complete solution would need to loop over all options.
Slide 7, three subgames example
G1 := {5||3|2}; G2 := {10|4||-2}; G3 := {7|6||1|0}
G := G1+G2+G3
G.LeftStop
G.RightStop
G.Options(Left) // note: it returns a set of one option; all others are dominated
// It is not so easy to tell which subgame they are from. But see the second example below.
G.Options(Right) // a set of two options
Slide 9, two subgames.
G1 := {5||3|2}; G2 := {10|4||-2}; G := G1+G2
G.LeftStop
G.RightStop
G1.LeftIncentives
G2.LeftIncentives
G.LeftIncentives // one dominating incentive. Only the one from G2
G1.RightIncentives
G2.RightIncentives
G.RightIncentives // G2 again has better incentive
G2.LeftIncentives.Head > G1.LeftIncentives.Head // better play in G2!
Examples for mean
4.Mean
{4|-4}.Mean
{6|-4}.Mean
{4||-4|-10}.Mean
{4||-4|-20}.Mean
CGSuite examples, try them out
{1|-1}
{2|-2}
{1|-1} + {2|-2}
{1|-1} + {2|-2} + {3|-3}
{1|-1} + {2|-2} + {3|-3} + {4|-4}
{1|-1} + {2|-2} + {3|-3} + {4|-4} + {5|-5}
{1|-1} + {2|-2} + {3|-3} + {4|-4} + {5|-5} + {6|-6}
{1|-1} + {2|-2} + {3|-3} + {4|-4} + {5|-5} + {6|-6} + {7|-7}
{1|-1} + {2|-2} + {3|-3} + {4|-4} + {5|-5} + {6|-6} + {7|-7} + {8|-8}
{1|-1} + {2|-2} + {3|-3} + {4|-4} + {5|-5} + {6|-6} + {7|-7} + {8|-8} + {9|-9}
Clobber examples:
game.grid.Clobber("OX").CanonicalForm
game.grid.Clobber("OXOXOX").CanonicalForm
game.grid.Clobber("OXOXOXOXOX").CanonicalForm
game.grid.Clobber("OXOXOXOXOXOXOX").CanonicalForm
game.grid.Clobber("OXOXOXOXOXOXOXOXOX").CanonicalForm
game.grid.Clobber("OXOXOXOXOXOXOXOXOXOXOX").CanonicalForm
There was a mistake on slide 20 of "comparing games", that we hit at the end of last class: in the game G = {0, ∗,−1|−1, {1|−2}, {2|0}}, everything I wrote about comparing options is true. In particular, −1 and {1|−2} are incomparable. However, the final statement is wrong: Canonical form: G = {0, ∗|−1, {1|−2}}. Why is it wrong? It is because of the other simplification, reversible moves. In this case, Right should never move to {1|−2}, since Left can immediately answer and move to 1, which is greater than G itself (because the Left options from G are "only" 0 and *). So the canonical form of G is {0, * | -1}, without that reversible Right option.
To make the example work as intended, and keep {1|−2} in the canonical form, the left options need to be better, so I replaced them by 2, 2 + * and made a new version of the slides with this fix. The canonical form of G:= {2, 2+*, -1 | -1, {1|-2}, {2|0}} is indeed {2, 2* | -1, {1 | -2} }. This is the kind of thing that is very easy for humans to miss, but CGSuite catches it easily.
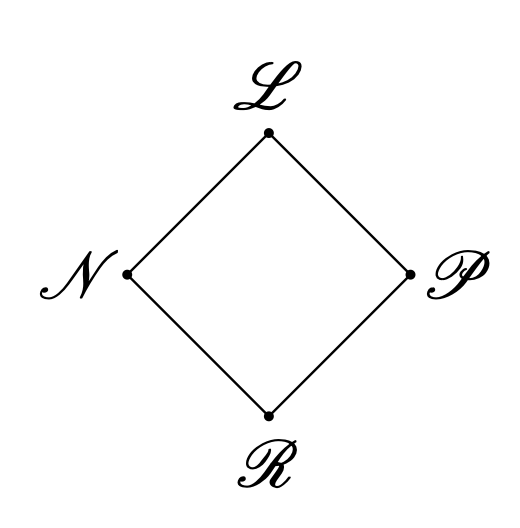
The outcome diamond is the partial order between game outcomes shown above (Figure from Urban Larsson's paper). If you have to choose a game based on its outcome, then as Left you always choose outcome L over any game with outcome in N, P, R, and you choose any other outcome over R, while outcomes N and P are incomparable.
However, that does not mean that e.g. any game in L is better than any game in another class in terms of direct comparison. For example, consider the games G = 1, and H = 100 | 0. Clearly, G is in L and H is in N, since Right can win H by moving to 0. So if left had to choose a single game, Left should choose G since it is a sure win, while H is not. However, G and H themselves are incomparable. There are many sums where having the option to move to H is more valuable than moving to G. For example, with game K = 0 | -50, the sum G + K is in N, but H + K is in L.
Thanks Abel!
White (students) is horizontal and goes first. This is with the "more-grid-games" branch of MCGS, which includes the rules of domineering.
Students played perfectly according to MCGS - all White to play positions are wins, and all Black to play positions are losses.
Moves (left square for White, top square for Black): 1. A2, 2. E5, 3. E4, 4. E1, 5. C2, 6. B5, 7. A4, 8. C5, 9.C4, 10. F2. Now horizontal has 4 more moves, and vertical only 3, so horizontal wins. Below are the calls to solve all game positions with MCGS.
./MCGS "[domineering] ......|......|......|......|......|...... {W}"
./MCGS "[domineering] ......|##....|......|......|......|...... {B}"
./MCGS "[domineering] ......|##....|......|......|....#.|....#. {W}"
./MCGS "[domineering] ......|##....|......|....##|....#.|....#. {B}"
./MCGS "[domineering] ....#.|##..#.|......|....##|....#.|....#. {W}"
./MCGS "[domineering] ....#.|#####.|......|....##|....#.|....#. {B}"
./MCGS "[domineering] ....#.|#####.|......|....##|.#..#.|.#..#. {W}"
./MCGS "[domineering] ....#.|#####.|......|##..##|.#..#.|.#..#. {B}"
./MCGS "[domineering] ....#.|#####.|......|##..##|.##.#.|.##.#. {W}"
./MCGS "[domineering] ....#.|#####.|......|######|.##.#.|.##.#. {B}"
./MCGS "[domineering] ....#.|######|.....#|######|.##.#.|.##.#. {W}"
Let *n denote a nim heap with n stones. We played the game *3 + *4 + *5. A winning move is to move from *3 to *1, leaving the sum *1 + *4 + *5. This is a losing position (2nd player win)
A few more examples of losing positions: *n + *n (second player copies the first player's moves), *1 + *2 + *3.
There is an analysis of this game based on the binary representation of heap sizes, and bitwise XOR. We will talk about it in class soon.
8-bit bitwise XOR a = 01101001 b = 10001110 --------------------- c = 11100111 c = a xor b
XOXOXO is a second player win. Thanks Abel for the picture!XOXOXOXOXO, in three tree nodes:
X can play to XOXOXO.XXO = XOXOXO + XXO.
Since XOXOXO is a second player win, no player can profit from playing there. So we can ignore that part and focus on XXO.
O to play has only one move, to XO.. From here, X to play can
clobber the last O stone and win.
XOXOXO + XXO to XXO.
Last update: Nov 28, 2025, Martin Müller