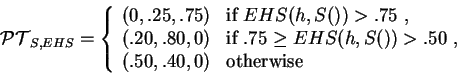Probability triple generation function

The PT generation function describes how a player should behave with a particular pair of cards in a specific situation. The function returns the probability distribution that, given a specific two-card hand and the public information about the state of the game, the action should be either fold, call, or raise.

$$f = P(\mbox{action = fold} \; \vert \; \mbox{pair of cards and game context})$$

$$c = P(\mbox{action = call} \; \vert \; \mbox{pair of cards and game context})$$

$$r = P(\mbox{action = raise} \; \vert \; \mbox{pair of cards and game context})$$

The function uses the hand evaluation in an expert-defined rule-based betting strategy to compute the three values. The hand evaluation comprises the strength and the potential of the hand; the strength represents the probability of the hand presently being the strongest one and the potential represents the probability of the hand becoming the strongest after future cards have been dealt (see [19]).

The first version of the PT generation function was a completely new betting strategy that was simpler than Loki-1's betting strategy. Although this function sufficed to show experimentally the advantages of having a non-deterministic betting strategy, it was outperformed by the old one. The main advantage of having a non-deterministic betting strategy is that we allow Loki-2 to randomly choose its action based on a set of probabilities rather than follow the single action returned by Loki-1's betting strategy.

The second attempt to create the PT function was to translate the strong, but rigid, betting strategy of Loki-1 into the PT scheme. A literal translation of the previous betting strategy into the PT function produced pure or deterministic probability triples. A pure PT has the value of the most likely action equal to one and the other two actions equal to zero. Once the PT function mimicked Loki-1's betting strategy, the boundaries between actions were smoothed by applying linear interpolation to create unpredictability.

With Loki-1's betting strategy in PT form, small modifications to the PT function, such as the one described in the previous paragraph, are less time consuming and the consequences of each change can be evaluated independently. By compartmentalizing the expert knowledge in a single routine, the design was improved by standard software engineering concepts. The benefits of the PT generation function are:

• it hides the poker specific details of the evaluation function from the rest of the system,
• it provides a well-defined interface,
• it confines the impact of changes in Loki-2's knowledge to a single function, and
• it facilitates the verification of changes.

To generate the PT for a hand, the hand value is computed first. The hand value is an estimate of the probability of winning. This value is then used by a set of rules to compute the probabilities of folding, calling and raising. Consider that S() gives the public information about a game, h is a hand, EHS(h, S()) gives the hand value, and $\mathcal{PT}_{S, EHS}(f,c,r)$ represents a PT generation function. An abstract view of a simplistic PT generation function is:

$$\mathcal{PT}_{S,EHS} = \left\{ \begin{array}{ll} (0,.25,.75)... ... }, \\ (.50,.40,0) & \text{otherwise} \\ \end{array}\right.$$

Note that one can add as many rules as needed to the PT generation function. Since all the knowledge is located in one single function, the addition of extra rules is a minor change in the program. In Figure 4.1 the algorithm for a simplified four-rule PT generation function is shown. The threshold values that define the likelihood of each action (param_postflopRaise and param_minToRaise) and the probabilities of each action for every case are defined by a poker expert and can be modified to vary Loki-2's playing style. Loki-2's PT generation function uses nine rules to produce the PTs used to choose an action in a game and eight rules to generate the PTs used in the opponent modeling module as a reweighting factor. When the PT generation function is called to determine a PT to select an action in the game, it considers rules containing more expert knowledge such as calling based on pot odds (the ratio of the amount of money in the pot to the amount of money it will cost us to call) and based on showdown odds (the ratio of the amount of money it will cost us to stay in the game to see the showdown to the amount of money we will make if we win in the showdown). During the reweighting process a simpler and faster PT generation algorithm is used. In addition, this PT generation function does not generate zero probabilities for an action, because we do not want to rule out any opponent's hand.

  

Figure 4.1: Pseudocode for a simplified PT generation function