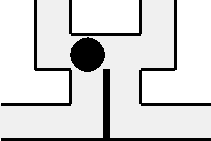
Figure 10: Thin Walled Device
The construction presented herein is clearly polynomial (linear) and so we have shown that Sokoban is PSPACE-complete. This answers the open question left in [1].
It is also easy to see that using the construction it is possible to build an infinite (i.e. a uniform extension) version of the puzzle in which only a finite number of boxes are not in storage, and that this version would be uncomputable by a reduction to the halting problem.
We point out that some simplification of our devices could be obtained if the barriers could be made thinner, that is if walls could be placed between grid points. For example, Subdevice One of figure 7 could be replaced by the device in figure 10.
Such thin wall design might make the design of popular puzzles easier and more interesting.
In addition to thinner walls, interesting puzzles might also be created by the addition of three dimensional underpasses. Note that our planar crossover construction, aside from being too clumsy for practical puzzle design, also does not allow boxes to be pushed through it. By allowing simple third dimension bridges, additional complexity could be built into small puzzles.
The instances of the puzzle that are popular usually require the boxes to move some distance to a set of contiguous storage locations. We wonder what the complexity of the puzzle would be under the constraint that all storage locations must be contiguous. Notice that under this constraint, the use of three dimensions to allow underpasses may be of particular importance.