number theory
(really) basic facts
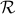

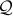
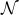
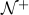
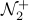
- counting
0 1 2 3 …
- rational
fractions
- real
represent a continuum on an infinitely long number line, with infinite-precision decimal representation
- irrational
real \ rational Π √2 …
>>> print (4*sum( 1.0/(4*x+1) - 1.0/(4*x+3) for x in range (0, 1000)))
- recall
a = b (mod n) means ∃ t ∈
 , a = b + t ⋅ n a = n ⋅ t + b
, a = b + t ⋅ n a = n ⋅ t + b- even
a = 0 (mod 2) ∃ t ∈
 , a = 2 ⋅ t
, a = 2 ⋅ t- odd
a = 1 (mod 2) ∃ t ∈
 , a = 2 ⋅ t + 1
, a = 2 ⋅ t + 1- odd iff (not even) ?
by division theorem
why school division algorithm works
∀ x ∈  , , |
∀ d ∈ 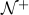 , , |
∃ unique q,r ∈  , , | ( x = q ⋅ d + r ) ∧ ( 0 ≤ r < d ) |
∀ x ∈  , , |
∃ unique q,r ∈  , , | ( x = q ⋅ 2 + r ) ∧ ( 0 ≤ r < 2 ) |
def divmsg(n,q,d,r):
print n,'=',q,'*',d,'+',r
def mydiv(n,d): #n>=0, d>0
q,r = 0,n
while r >= d:
q,r = q+1, r-d
divmsg(n,q,d,r)
def mydiv2(n,d): #n>=0, d>0
if n==0:
q,r = 0,0
divmsg(n,q,d,r)
return 0,0
q,r = mydiv2(n/2,d)
q,r = 2*q, 2*r
if 1==n%2:
r = r+1
if r >= d:
q,r = q+1, r-d
divmsg(n,q,d,r)
return q,r
import random
for _ in range(10):
n = random.randint(500,1000)
d = random.randint(1,9)
mydiv2(n,d)
# loop, so use variant, invariant
def mydiv(n,d): #n>=0, d>0
q,r = 0,n
while r >= d:
# variant: r
# invariant: n == qr + d
q,r = q+1, r-d
divmsg(n,q,d,r)
#python tip: use assert to check invariant
def divmsg(n,q,d,r):
assert(n==q*r+d)
print n,'=',q,'*',d,'+',r
# recursion, so argue by induction on n # use same invariant
⇒
x odd, so ∃ j ∈  , x = 2j + 1,
, x = 2j + 1,
y odd, so ∃ k ∈  , y = 2k + 1, so
, y = 2k + 1, so
xy = (2j + 1)(2k + 1) = 2(2jk + k + j) + 1, so
∃ q (= 2jk + k + j), xy = 2q + 1 so
xy is odd
⇐
assume ~(x,y odd)
want to show ~(xy odd)
…
x odd ⇒ xt odd
proof by induction (sketch)
base case: let t = 0, then …
inductive case: assume claim holds
for an arbitrary value of t,
say t = k ≥ 0
then xk+1 = x ⋅ xk = (odd) ⋅ (odd) = odd, …
- x,y odd implies x+y even
primes
every integer n ≥ 2 is a product of primes
proof by induction (sketch)
base case: let n = 2, then …
inductive case: assume thm holds for
all integers from 2 up to an arbitrary n ≥ 2, say n = k
k+1 prime? done
k+1 not prime? then k+1 = xy, where 2 ≤ x < k+1 and 2 ≤ y < k+1, so
by ind. hyp., x,y each a product of primes, so
k+1 = xy = (product of primes)⋅(product of primes), so a product of primes
every integer n ≥ 2 can be written uniquely as
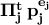 , with
, with 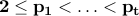
book 7, proposition 30
prime p, integers x,y, p|xy → p|x or p|y
-
use induction, division theorem, prime factorization
prime p | n2 ⇒ p2 | n2 ⇒ p | n
why ? n a product of powers of primes ⇒
n2 a product of even powers of primes
there are many primes
lemma n ≥ 2, n divides x⋅y ⇒ n does not divide x⋅y + 1
why? hint: n divides xy means xy = 0 (mod n) …
lemma S = { p1, ... , pt } prime ⇒ p1 × ... × pt + 1 has prime factor not in S
theorem infinitely many primes
proof by contradiction (sketch)
assume S = { p1, ... , pt } is all primes use lemma
root 2 irrational
assume √2 = a/b with a,b rational b ≥ 2 (why ?)
can assume a,b have no common divisor (why ?)
2 = (√2)2 = (a/b)2 = a2/b2 so 2 b2 = a2
so (by corollary) 2 | a
so a = 2t so 2 b2 = (2t)2 = 4t2
so b2 = 2t2 so (by corollary) 2 | b
contradiction
counting
0 1/1
1 2 2/1 1/2
3 4 5 3/1 2/2 1/3
6 7 8 9 4/1 3/2 2/3 1/4
10 11 12 13 14 5/1 4/2 3/3 2/4 1/5
... ...
list: not in list: 0.000000... 0.1 0.111111... 0 0.010101... 1 0.101010... 1 0.110110... 0 0.001001... 0 ... ...
mod arith. and remainders
⇒ x = tn + r y = sn + r x-y = tn - sn = (t-s)n
⇐ … contrapositive … assume x ≠ y (mod n)
x = qn + r
y = vn + r’
0 ≤ r,r’ ≤ n-1
r ≠ r’
x-y = qn+r - vn+r’ = (q-v)n + (r-r’)
1-n < r-r’ < n-1 (why?) and r-r’ ≠ 0, so
n does not divide r-r’ so
n does not divide x-y
x+y = x’+y’ (mod n)
Pf.
x = x’ (mod n) ⇒ x-x’ = tn for some integer t
y = y’ (mod n) ⇒ y-y’ = sn for some integer s
so x+y - (x’+y’) = x-x’ + y-y’ = tn + sn = (t+s)n
so x+y = x’+y’ (mod n) QED
x-y = x’-y’ (mod n)
Pf. exercise
x ⋅ y = x’ ⋅ y’ (mod n)
Pf. exercise
113 * (167 + 484) + 192 * 145 (mod 21) = ?
113 * ( 651 ) + 192 * 145 (mod 21) =
113 * ( 651 ) + 27840 (mod 21) =
73563 + 27840 (mod 21) =
101403 (mod 21) =
15 (mod 21)
efficient: 113=8 167=-1 484=1 192=3 145=-2
8 * (-1 + 1 ) + 3 * (-2) (mod 21) =
0 + -6 (mod 21) =
15 (mod 21)
floor, ceiling
largest integer ≤ x
tip
∀ n ∈  , ∀ x ∈
, ∀ x ∈ 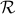 ,
,
n = 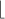 x
x 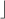 ⇔ ∃ ε ∈
⇔ ∃ ε ∈ 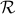 , 0 ≤ ε < 1, x = n + ε
, 0 ≤ ε < 1, x = n + ε
smallest integer ≥ x
tip
∀ n ∈  , ∀ x ∈
, ∀ x ∈ 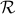 ,
,
n = 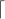 x
x 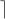 ⇔ ∃ ε ∈
⇔ ∃ ε ∈ 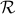 , 0 ≤ ε < 1, x = n - ε
, 0 ≤ ε < 1, x = n - ε
Pf. let t = 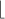 x
x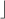 by tip, ∃ ε ∈
by tip, ∃ ε ∈ 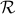 , 0 ≤ ε < 1, x = t + ε
, 0 ≤ ε < 1, x = t + ε
so n + x = n + t + ε = m + ε where ε ∈
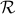 , 0 ≤ ε < 1, m = n + t ∈
, 0 ≤ ε < 1, m = n + t ∈ 
so, by tip, m = 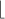 n+t
n+t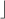 QED
QED
∀ x ∈
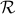 , ∀ n ∈
, ∀ n ∈  ,
,
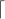 n+x
n+x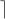 = n +
= n + 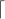 x
x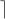
∀ x ∈
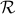 ,
, 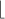 x
x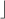 = -
= -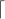 -x
-x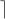
∀ x ∈
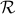 ,
,
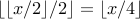 hint: 4 cases, consider x mod 4
hint: 4 cases, consider x mod 4
gcd
d is divisor of n (write: d | n )
if d ≠ 0, n,d ∈  , ∃ t ∈
, ∃ t ∈  , n = t ⋅ d
, n = t ⋅ d
g is greatest common divisor of x,y (write: g =gcd(x,y) ) if g is largest integer d s.t. d|x, d|y
divisors of -6 ?
-6, -3, -2, -1, 1, 2, 3, 6
divisors of 15 ?
-15, -5, -3, -1, 1, 3, 5, 15
common divisors of -6,15 ?
-3, -1, 1, 3
gcd(-6,15) ?
3
d|x, d|y ⇒ ∀ a,b ∈  , d|(a⋅x + b⋅y)
, d|(a⋅x + b⋅y)
proof
∃ s,t ∈  , x = s⋅d, y = t⋅d
, x = s⋅d, y = t⋅d
⇒ a⋅x + b⋅y = a⋅(s⋅d) + b⋅(t⋅d) = (a⋅s + b⋅t)⋅d,
⇒ ∃ w ∈  , a⋅x + b⋅y = w⋅d,
, a⋅x + b⋅y = w⋅d,
⇒ d | a⋅x + b⋅y,
QED
least common multiple
k is least common multiple of x,y (write: k =lcm(x,y) ) ⇔
k is least positive integer t s.t. x|t, y|t
multiples of -6 ?
…, -18, -12, -6, 0, 6, 12, 18, …
multiples of 15 ?
…, -45, -30, -15, 0, 15, 30, 45, …
common multiples of -6,15 ?
…, -60, -30, 0, 30, 60, …
lcm(-6,15) ?
30
x = 6 = 2^1 * 3^1 * 5^0 y = 15 = 2^0 * 3^1 * 5^1 x*y = 90 = 2^1 * 3^2 * 5^1 gcd(x,y) = 2^0 * 3^1 * 5^0 = 3 lcm(x,y) = 2^1 * 3^1 * 5^1 = 30 gcd*lcm = 2^1 * 3^2 * 5^1 = 90
gcd computation
let x,y ∈ 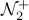 x = Πj pj xj y = Πj pj yj
x = Πj pj xj y = Πj pj yj
where p1, ... , pt are prime divisors of x ⋅ y then
gcd(x,y) = Πj pj min(xj,yj)
lcm(x,y) = Πj pj max(xj,yj)
gcd(x,y) ⋅ lcm(x,y) = Πj pj min(xj,yj)+max(xj,yj) = Πj pj xj + yj = x ⋅ y
def gcdSlow(x,y): # 1 <= x,y
if x > y:
print ' = gcdSlow(', y, x, ')'
return gcdSlow(y,x)
elif x == y:
print ' = ',x
return x
else: # 1 <= x < y
print ' = gcdSlow(', x, y-x, ')'
return gcdSlow(x,y-x)
>>> gcdSlow(99,131)
= gcdSlow( 99 32 )
= gcdSlow( 32 99 )
= gcdSlow( 32 67 )
= gcdSlow( 32 35 )
= gcdSlow( 32 3 )
= gcdSlow( 3 32 )
= gcdSlow( 3 29 )
= gcdSlow( 3 26 )
= gcdSlow( 3 23 )
= gcdSlow( 3 20 )
= gcdSlow( 3 17 )
= gcdSlow( 3 14 )
= gcdSlow( 3 11 )
= gcdSlow( 3 8 )
= gcdSlow( 3 5 )
= gcdSlow( 3 2 )
= gcdSlow( 2 3 )
= gcdSlow( 2 1 )
= gcdSlow( 1 2 )
= gcdSlow( 1 1 )
= 1
def gcd(x,y): # 0 <= x 1 <= y
if x == 0:
print ' = ',y
return y
else:
print ' = gcd(', y%x, x, ')'
return gcd(y%x,x)
>>> gcd(99,131)
= gcd( 32 99 )
= gcd( 3 32 )
= gcd( 2 3 )
= gcd( 1 2 )
= gcd( 0 1 )
= 1
gcd minimax theorem
S,T ⊂  exists x ∈ S ∩ T ∀ s ∈ S, ∀ t ∈ T, s ≤ t
exists x ∈ S ∩ T ∀ s ∈ S, ∀ t ∈ T, s ≤ t
⇒ x = max(S) = min(T)
proof:
x ∈ S ⇒ ∀ t ∈ T, x ≤ t,
also x ∈ T so x = min(T)
similarly (exercise) x = max(S)
∀ x,y ∈  , x,y not both 0
, x,y not both 0
D = { common divisors of x,y }
L+ = { ax + by | a,b ∈  , ax + by > 0 }
, ax + by > 0 }
⇒ (1) ∀
d ∈ D, ∀ f ∈ L+, d ≤ f
⇒ (2) ∃ g ∈ D ∩ L+
⇒ (3) min(L+) = max(D) = gcd(x,y)
d | x ⇒ ∃ s ∈  , x = sd
, x = sd
d | y ⇒ ∃ t ∈  , y = td
, y = td
∃ a,b ∈  , f = ax + by ⇒ f = a(sd) + b(td) = (as + bt)d = qd ⇒ d | f
, f = ax + by ⇒ f = a(sd) + b(td) = (as + bt)d = qd ⇒ d | f
if d ≤ 0 then d < f
if d > 0 then d,f > 0 so q = f/d > 0 and q ∈  so f/d =q ≥ 1 so d ≤ f WOOHOO!
so f/d =q ≥ 1 so d ≤ f WOOHOO!
assume 0 ≤ |x| ≤ |y| (swap x,y if necessary)
case 0 = x < |y| (recall x,y not both 0)
⇒ |y| ∈ D ∩ L+
case 0 < |x| = |y|
⇒ |y| ∈ D ∩ L+
case 0 < |x| < |y|
assume (2) holds for all smaller values of |x|+|y|
let E = common divisors of |x|,|y|-|x|
claim: D = E (exercise: prove this)
let M+ = positive linear combinations of |x|,|y|-|x|
claim: L+ = M+ (exercise: prove this)
by ind. hyp., ∃ g ∈ E ∩ M+ (why ?)
E ∩ M+ = D ∩ L+, so ∃ g ∈ D ∩ L+ WOOHOO!
by (2) and the lemma WOOHOO!
gcd minimax example (extended euclid alg'm)
gcd(489,90) = ?
489 90 39 12 3 0
5 2 3 4
-38 7 -3 1 0
3 = 39 - 3*12
= 39 - 3*(90 - 2*39)
= 7*39 - 3*90
= 7*(489 - 5*90) - 3*90
= 7*489 - 38*90
another gcd minimax example
gcd(7484,5108) = ?
7484 5108 2376 356 240 116 8 4 0
1 2 6 1 2 14 2
904 -617 287 -43 29 -14 1 0
4 = 7484*-617 + 5108*904
extended euclid gcd verification
let a = 187326503
let b = 474659731
let g = 91
claim: g = gcd(a,b)
proof:
a = g * 2058533
b = g * 5216041
let c = 1833473
let d = -723588
notice g = a*c + b*d
now use gcd minimax theorem QED
def myprint(f,g,h,i,j):
assert(f*g+h*i==j); assert(f%j==0); assert(h%j==0)
print f,h,":",f,'*',g,'+',h,'*',i,'=',j
def exteuclid(a,b): #a>=b>=0: x,y,d: ax+by=d=gcd(x,y)
if b==0:
myprint(a,1,b,0,a)
return 1, 0, a
q, r = a/b, a%b
x, y, d = exteuclid(b, r)
myprint(a, y, b, x-q*y, d)
return y, x - q*y, d
exteuclid(1203,891)
3 0 : 3 * 1 + 0 * 0 = 3
42 3 : 42 * 0 + 3 * 1 = 3
45 42 : 45 * 1 + 42 * -1 = 3
267 45 : 267 * -1 + 45 * 6 = 3
312 267 : 312 * 6 + 267 * -7 = 3
891 312 : 891 * -7 + 312 * 20 = 3
1203 891 : 1203 * 20 + 891 * -27 = 3
euclid gcd worst case
import cmath
def gcdIt(y,x):
n = 0
while x != 0:
tmp = y % x
y = x
x = tmp
n += 1
return y, n
def fib(n):
a, b = 0, 1
for i in range(n):
a, b = b, a + b
return a
goldenratio = (1.0+cmath.sqrt(5))/2.0
a = 10
z = fib(a)
w = fib(a-1)
print gcdIt(z,w)
print cmath.log(z,goldenratio)
euclid gcd average case
import cmath #http://mathworld.wolfram.com/EuclideanAlgorithm.html #Heilbronn estimate heilbronn = 12*cmath.log(2)/(cmath.pi*cmath.pi) def avgEstimate(n): return heilbronn*cmath.log(n) #number of iterations of gcd(y,x) def gcdIt(y,x): iterations = 0 while x != 0: tmp = y % x y = x x = tmp iterations += 1 return iterations #n'th fibonacci number def fib(n): a, b = 0, 1 for i in range(n): a, b = b, a + b return a #average of gcd(1,n)... gcd(n,n) def avgIt(n): sum = 0 for j in range(n): sum = sum+gcdIt(n,j+1) return 1.0*sum/(1.0*n) #compare average with Heilbronn estimate for j in range(5,30): fj = fib(j) print j, fj, avgIt(fj), avgEstimate(fj)
modular exponentiation
def mod_exp(a,e,n): # 0 < a,e 2<= n
if e == 1:
return a%n
elif e%2 == 0:
return ( mod_exp(a,e/2,n)**2 )%n
else:
return ( mod_exp(a,e/2,n)**2 * a)%n
def mod_exp_display(a,e,n): # 0 < a,e 2<= n
if e == 1:
x = a
print a,'^',e,'= ',x%n
elif e%2 == 0:
x = mod_exp_display(a,e/2,n)**2
print a,'^',e,'= (',a,'^',e/2,')^2 =',x%n
else:
x = mod_exp_display(a,e/2,n)**2 *a
print a,'^',e,'= (',a,'^',e/2,')^2 *',a,'=',x%n
return x%n
mod_exp_display(3,11549,17) 3 ^ 1 = 3 3 ^ 2 = ( 3 ^ 1 )^2 = 9 3 ^ 5 = ( 3 ^ 2 )^2 * 3 = 5 3 ^ 11 = ( 3 ^ 5 )^2 * 3 = 7 3 ^ 22 = ( 3 ^ 11 )^2 = 15 3 ^ 45 = ( 3 ^ 22 )^2 * 3 = 12 3 ^ 90 = ( 3 ^ 45 )^2 = 8 3 ^ 180 = ( 3 ^ 90 )^2 = 13 3 ^ 360 = ( 3 ^ 180 )^2 = 16 3 ^ 721 = ( 3 ^ 360 )^2 * 3 = 3 3 ^ 1443 = ( 3 ^ 721 )^2 * 3 = 10 3 ^ 2887 = ( 3 ^ 1443 )^2 * 3 = 11 3 ^ 5774 = ( 3 ^ 2887 )^2 = 2 3 ^ 11549 = ( 3 ^ 5774 )^2 * 3 = 12