greedy algorithms

mst Prim Kruskal union-find K correct K complete better UF

mst

minimum spanning trees

notes on msts, kruskal correctness, kruskal completeness
definitions
- graph, path, connected, component, cycle, forest, tree, spanning, weighted graph, mst
tree properties
- removing cycle edge does not change components
  - why?
- tree with at least 2 nodes has at least 2 nodes with degree 1
  - ends of longest path
- tree with n nodes has n-1 edges
  - induction, ends of longest path
- connected, n node, n-1 edges implies tree
  - must be node with degree 1
- tree if and only if, between each node pair, unique path
  - ends of longest path
- T spanning tree of G, e not in T, then
  - T+e has cycle C
  - for every c in C, T+e-c spanning tree
  - if T mst, then w(e) ≥ w(c)
- X edge subset of mst T, S node subset of V such that no x crosses cut (S,V-X), e lightest edge across cut, then X+e edge subset of mst T’

Prim's mst

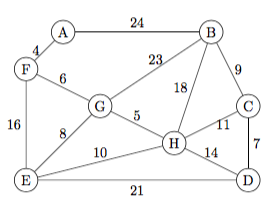
a weighted digraph D

trace Prim from E
            A    B    C    D    E    F    G    H
tree                            *
E update                  21 E  *   16 E  8 E 10 E
GE 8                            *         *
G update        23 G      21 E  *    6 G  *    5 G
HG 5                            *         *    *
H update        18 H 11 H 14 H  *    6 G  *    *
FG 6                            *    *    *    *
F update    4 F 18 H 11 H 14 H  *    *    *    *
AF 4        *                   *    *    *    *
A update    *   18 H 11 H 14 H  *    *    *    *
CH 11       *         *         *    *    *    *
C update    *    9 C  *    7 C  *    *    *    *
DC 7        *         *    *    *    *    *    *
D update    *    9 C  *    *    *    *    *    *
BC 9        *    *    *    *    *    *    *    *

simple Prim mst
def prim(G,source):
  cost, parent, fringe = {}, {}, []
  infin = weighted.infinity(G)
  for v in G:
    cost[v], parent[v] = infin, -1
    fringe.append(v)
  cost[source],parent[source] = 0, source

  sum = 0
  print source, 'start'
  while len(fringe)>0:
    u = fringe.pop(weighted.indexOfMin(fringe,cost))
    sum += cost[u]
    if u != source: print u,parent[u],cost[u]
    if cost[u] == infin:  doneEarly = True
    for (v,costuv) in G[u]:
      if (v in fringe) and (cost[v] > costuv):
        cost[v] = costuv
        parent[v] = u
  print 'mst weight', sum

prim(weighted.G4,'A')

Kruskal's mst

a weighted digraph D

trace Kruskal
AF 4
GH 5
FG 6
CD 7
EG 8
BC 9
reject EH
CH 11
reject DH
reject EF
reject BH
reject DE
reject BG
reject AB

implementing Kruskal

what component are you in?
what component are you in?
merge components containing x,y
leads to a union-find data structure
simplest implementation
- component: tree, with parent pointers
- find(a): return root of tree containing a
- union(a,b): parent[root(a)] = root(b)

simple union find data structure

def myfind(v,P): # simple find
  while P[v] != v:
    v = P[v]
  return v

def myunion(x,y,P): # simple union
  rootx, rooty = myfind(x,P), myfind(y,P)
  P[rootx] = rooty

simple Kruskal
import weighted, UF
# convert from weighted adjacency list
#         to tuple list:   (v,w,wt_vw)
def createEdgeList(G):
  L = []
  for v in G:
    for (w,wt) in G[v]:
      if ord(v)<ord(w): L.append((v,w,wt))
  return L

# extract tuple with min wt
def extractmin(L):
  ndxMin, valMin = 0, L[0][2]
  for j in range(1,len(L)):
    t = L[j]
    if t[2] < valMin:
      ndxMin, valMin = j, t[2]
  return L.pop(ndxMin)

def kruskalDemo(G):
  L = createEdgeList(G)
  parent = {}
  for v in G: parent[v] = v

  while len(L) > 0:
    t = extractmin(L)
    a, b = t[0], t[1]
    ra, rb = UF.myfind(a,parent), UF.myfind(b,parent)
    print a, ra, b, rb,
    if ra != rb:
      print 'add edge',a,b,t[2]
      UF.myunion(ra,rb,parent)
    else:
      print 'reject  ',a,b

kruskalDemo(weighted.G4)

trace: Kruskal with union/find data structure
a r b s    r,s: roots of UF comp'ts with a,b
                     parent
                     A B C D E F G H
A A F F add A F 4    F B C D E F G H
G G H H add G H 5    F B C D E F H H
F F G H add F G 6    F B C D E H H H
C C D D add C D 7    F B D D E H H H
E E G H add E G 8    F B D D H H H H
B B C D add B C 9    F D D D H H H H
E H H H reject   E H
C D H H add C H 11   F D D H H H H H
stop: n-1 edges
final UF structure:              H
                           F   G   E   D
                           A          C B

Kruskal mst correctness

Claim: tree returned by Kruskal is mst.
Proof (sketch)
- at each step, set of picked edges is acyclic, so a forest.
- number of components of n-node m-edge acyclic forest is n-m (exercise: PBI)
- so, when number picked edges < n-1, still ≥2 components. since input graph connected, must be an edge in input graph with ends different forest components. so, K's alg can pick some edge.
- so K's alg picks n-1 edges, leaving acyclic graph, n nodes, 1 component, so spanning acyclic component, so spanning tree.
Claim: the tree returned is an MST.
Proof (sketch):
- Let T be the tree returned by Kruskal's algorithm. Let T* be an MST. If T=T* we are done, so assume T ≠ T*.
- Label the edges of T 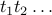in the order they are selected by Kruskal's algorithm, i.e. non-decreasing weight.
- Let k be the smallest index such that 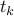is not in T*.
- Notice that T* 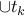has a cycle C containing 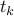, and that removing any edge of C leaves a spanning tree
  - why? because the resulting graph is connected, and has n-1 edges
- Notice that C contains at least one edge t* that is not in T
  - why? because T is a tree, so acyclic
- Notice that the weight of every such t* is at least the weight of
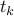
  - why? because t* does not form a cycle with edges 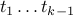$t_1 ldots t_{k-1}$ , which are all in T*, and yet Krusal picked 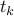instead of t*
- Notice that the weight of every such t* is at most the weight of
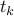
  - why? because T' = T* -t* + 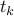is a spanning tree, with weight wt(T*) - wt(t*) + wt(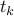), so if wt(t*) > wt(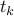) then wt(T') < wt(T*), contradiction since T* is an MST
- so, for every such t*, wt(t*) = wt(
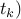
- pick any t*, and let T' = T* -t* +
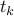
- notice T' is an MST, with one more edge of T than T*
- so repeating the above process as necessary, we eventually find an MST that contains all the edges of T, i.e. that equals T.

Kruskal mst completeness

every mst is kruskal

recall: in each step of K's algm, any min-cost candidate edge can be added to the tree-so-far
call an mst kruskal if it is found by some execution of K's algm
claim: every mst is Kruskal

proof: by induction, contradiction form: consider an arbitrary mst T of a graph G. among all possible Kruskal executions on G, consider the one that yields the Kruskal mst K that maximizes the initial sequence of edges that are in T. say the sequence of edges of this execution is S=( k₁, ..., k_n-1) . so these edges form the mst K.

let q be smallest index such that k_q is not in T.

T+k_q has a unique cycle C. The edges of A={ k₁, ..., k_q } are picked by Kruskal, so acyclic, so C includes some edge not in A, say c.

k_q is a max weight edge on C. But Kruskal picks k_q before c, so k_q weighs no more than c. So k_q weighs the same as c.

So Kruskal could have picked c instead of k_q. So some execution of Kruskal starts by selecting the edge sequence ( k₁, ..., k_q ) , contradicting our choice of K.

better UF

Kruskal UF structure: can we do beter?
what is total cost of these operations?

union(A B)  union(B C)  union(C D) ... union(Y Z)
find(A) find(B) find(A) find(D) ... find(A) find(Z)

motivation: keep UF trees shorter

two options: union-by-rank, or find-grandparent-compress

better UF
def findGP(x, parents): # find, gp compress
  px = parents[x]
  if x==px: return x
  gx = parents[px] # grandparent
  while px != gx:
    parents[x] = gx
    x = px ; px = gx ; gx = parents[gx]
  return px

def unionBR(v,w,P,R): # union by rank
  rv,rw = myfind(v),myfind(w)
  if   R[rv] < R[rw]:
    P[rv] = rw
  elif R[rv] > R[rw]:
    P[rw] = rv
  else:
    P[rv] = rw
    R[rw] += 1

min cuts: randomized algorithm

min cut of a graph: cut (S,V-S) that minimizes number of cross edges
brute force algorithm: consider all 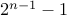$2^{n-1}-1$ possible cuts
Karger's randomized algm:
- single iteration: Kruskal (except select edges at random), stop after 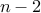edges
- with prob. at least 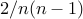, cut is min
- perform 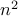iterations, take smallest cut, with high prob is min

Karger: prob cut min at least 2/n(n-1)

consider min cut, say size
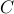
on first step, 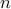components
- each component incident 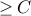edges
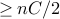- so edges
- Prob(picking edge from )
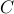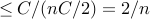
when 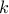components
- each component incident 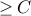edges
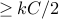- so edges
- if so far have missed ,
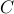  Prob(picking edge from )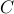
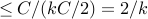
prob(avoiding each time)
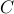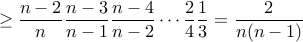
$geq displaystyle frac{n-2}{n}frac{n-3}{n-1}frac{n-4}{n-2}cdotsfrac{2}{4}frac{1}{3} = frac{2}{n(n-1)}$

Karger: an example

consider the graph with vertices A to F and edges AB AC BC DE DF EF plus AD
uniqe min cut {A B C} {D E F} has size 1 (edge AD)
probability that Karger's algorithm finds this cut?
to find this cut, must pick 2 edges from each of 2 triangles
prob that first edge from a triangle: 6/7
prob that second edge from a triangle: 5/6
two cases:
- i) prob 2/5: one triangle has 1 edge remaining, the other 3
- ii) prob 3/5: each triangle has 2 edges remaining
prob third edge from a triangle: i) 3/4 (one of 5 remaining edges would create a cycle if picked) ii) 4/5
- prob fourth edge from a triangle: 2/3 (one of 4 remaining edges would create a cycle if picked)
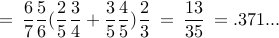
total prob $displaystyle = : frac{6}{7}frac{5}{6} (frac{2}{5}frac{3}{4} + frac{3}{5}frac{4}{5}) frac{2}{3} : = : frac{13}{35} : = .371...$
general bound ? 6-vertex graph, prob $displaystyle geq : frac{2}{6*5} : = : frac{1}{15} : = : .066...$

randomized min cut
import random

def myfind(x, parents):
  if x==parents[x]: return x
  return myfind(parents[x],parents)

def myunion(x,y,parents):
  parents[x] = y

def nodeedgecount(G):
  n,m = 0,0
  for v in G:
    n+= 1
    for w in G[v]:
      if v < w: m+= 1
  return n,m

def edgelist(G):
  L = []
  for v in sorted(G):
    for w in G[v]:
      if v < w: L.append((v,w))
  return L

def cutedges(E,P):
  edgeset = []
  for e in E:
    if myfind(e[0],P) != myfind(e[1],P):
      edgeset.append(e)
  return edgeset

def makeparents(G):
  p = []
  for v in sorted(G):
    p.append(v)
  return p

def randomcut(G,n,E):
  edgesadded = 0
  P = makeparents(G)
  for e in E:
    x = myfind(e[0],P)
    y = myfind(e[1],P)
    if x != y:
      myunion(x,y,P)
      edgesadded += 1
      if edgesadded == n-2:
        return cutedges(E,P)

def showgoodcuts(G,t):
# iterate t times; show cut every time it improves
  n,m = nodeedgecount(G)
  E = edgelist(G)
  bestcutsize = m+1 # initialize with impossible value
  for j in range(t):
    random.shuffle(E)
    C = randomcut(G,n,E)
    if len(C) < bestcutsize:
      bestcut = C
      bestcutsize = len(bestcut)
      print 'iteration',j,bestcut

G = {0:[1,2,3], 1:[0,2,3], 2:[0,1,3,4], 3:[0,1,2,5],
     4:[2,5,6,7], 5:[3,4,6,7], 6:[4,5,7], 7:[4,5,6] }

showgoodcuts(G,10)

Huffman encoding

wiki