divide and conquer
take Θ( f(n) ) runtime algorithm
divide into k subproblems
recombine with Θ( g(n) ) method, where g(n) = o(f(n))
result: o( f(n) ) algorithm
multiplication
(a bi)(c di) = (ac-bd) (bc + ad)i 4 mult, 2 add/sub x: ac y: bd z: (a+b)(c+d) (a bi)(c di) = (x-y) (z-x-y)i 3 mult, 5 add/sub
def bitlength(n): return len(bin(n))-2
def leftright(x,n): # x > 1
left = x >> n/2
right = x - (left << n/2)
return left, right
def fastmul(x,y): # x,y > 0
n = bitlength(x)
if n <= 4:
return x*y
xl, xr = leftright(x,n)
yl, yr = leftright(y,n)
pl = fastmul(xl,yl)
pr = fastmul(xr,yr)
pm = fastmul(xl+xr,yl+yr)
return (pl << 2*(n/2)) + ((pm - pl - pr) << n/2) + pr
for j in range(400):
for k in range(400):
assert( fastmul(j,k) == j*k)
- assume 7 digit inputs
- shift <- 7/2 = 3
- split inputs: aaaa bbb cccc ddd
- a' b' c' d'
- L <- a' * c'
- R <- b' * d'
- S <- (a' + b') * (c' + d')
- return L * base^(2*shift) +
(S-L-R) * base^shift +
R
- correct ?
aaaa bbb
* cccc ddd
--------
llllllll mmmmmmm rrrrrr
a'c' a'd'+b'c' b'd'
- want L = a'c' check :)
- want R = b'd' check :)
- want M = S-L-R = b'c' + a'd' ???
S-L-R = a'c' + b'c' + a'd' + b'd - a'c' - b'd'
= b'c' + a'd' check :)
return x*y if x <= 10 or y <= 10
(1234,5678)
(12,56)
(1,5) 5
(2,6) 12
1+2,5+6
(3,11) 33
5 33-5-12 12
500 + 160 + 12
672
(34,78)
(3,7) 21
(4,8) 32
3+4,7+8
(7,15) 105
21 105-21-32 32
2100 + 520 + 32
2652
12+34,56+78
(46,134)
(4,13) 52
(6,4) 24
4+6,13+4
(10,17) 170
52 170-52-24 24
5200 + 940 + 24
6164
672 6164-672-2652 2652
6720000 + 284000 + 2652
7006652
T(n) = 3T(n/2) + O(n)
will see T(n) = O(nlg 3) = O(n1.58..)
O(n2) school, peasant
O(nlg 3) Karatsuba
O(nlog35) Toom-Cook 3-way
O(nlog n log log n) Schonhage-Strassen
O(nlog n 2O(log * n)) Furer
in practice, faster algorithms not worth it unless n large
python uses school for small n, Karatsuba for large n
recurrence relations
integers a>0, b>1, real d≥0, T(n) = a T(n/b) + O(nd),
if bd > a ( d > lgb a ) then T(n) ∈ O(nd)
if bd = a ( d = lgb a ) then T(n) ∈ O(nd lg n)
if bd < a ( d < lgb a ) then T(n) ∈ O(nlgba)
assume
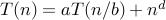 for
for 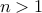
assume
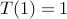
assume
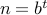
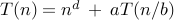
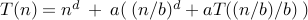
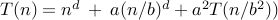
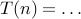
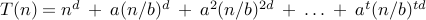
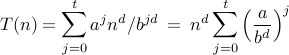
let
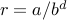
if
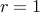
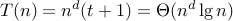
if
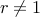
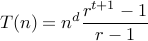
if
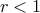
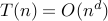
if
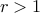
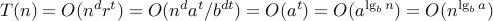
T(n) = 3 T(n/2) + O(n)
a=3 b=2 d=1 T(n) ∈ O(nlg 3) = O(n1.58..)
search/sort
key a list item
usual performance measure: count key comparisons
e.g. binary search, key comparisons
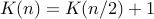
master theorem: a=1, b=2, d=0, so
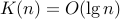
to accurately measure binary search runtime, need to know
how big are numbers in list ?
how is division by 2 implemented ?
how is key comparison implemented ?
e.g. each list item: {1,…,m}, div2: shift, compare: subtract
then
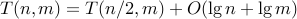
def ms(x): # based on:
#http://stackoverflow.com/questions/18761766/mergesort-python
result = []
if len(x) < 2:
return x
mid = len(x)/2 ; y = ms(x[:mid]) ; z = ms(x[mid:])
i,j = 0,0
while i < len(y) and j < len(z):
if y[i] > z[j]:
result.append(z[j]) ; j += 1
else:
result.append(y[i]) ; i += 1
result += y[i:] + z[j:]
return result
def select(L,k):
A = []; B = []; C = []
v = L[random.randint(0,len(L)-1)]
for j in L:
if j<v:
A.append(j)
elif j>v:
C.append(j)
else:
B.append(j)
if k <= len(A):
return select(A,k)
if k <= len(A) + len(B):
return v
return select(C,k-len(A)-len(B))
worst case:
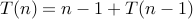 so
so 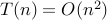
best case:
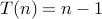
average case:
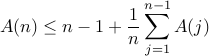
prove by induction:
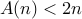 , so
, so 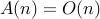
# partition, qs:http://hetland.org/coding/python/quicksort.html
def partition(list, start, end):
pivot = list[end] # partition around the last value
bottom = start-1 # initially outside sublist to be partitioned
top = end # " "
done = 0
while not done: # until all elements partitioned...
while not done: # until we find an out of place element...
bottom = bottom+1 # move the bottom up.
if bottom == top: # if hit top...
done = 1 # ... we are done.
break
if list[bottom] > pivot: # bottom out of place?
list[top] = list[bottom] # put it at top...
break # ... resume search from top
while not done: # until we find an out of place element...
top = top-1 # move top down.
if top == bottom: # if hit bottom...
done = 1 # ... we are done.
break
if list[top] < pivot: # top out of place?
list[bottom] = list[top] # put it at bottom...
break # ... resume search from bottom
list[top] = pivot # replace pivot
return top # return split index
def quicksort(list, start, end):
if start < end: # two or more elements?
split = partition(list, start, end)
quicksort(list, start, split-1)
quicksort(list, split+1, end)
return
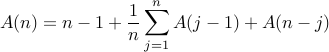
can show
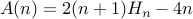 , where
, where 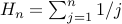
so
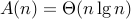
improvements
pick splitter to be median of L[1], L[n/2], L[n]
recursively sort smaller subproblem (so
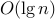 stack depth),
eliminate remaining tail recursion
stack depth),
eliminate remaining tail recursion
sorting lower bound
only operation allowed on keys: <
e.g. allowed L[19] < L[27] ?
e.g. not allowed L[19] > (L[27] + L[92]) ?
consider decision tree: after 1st comparison, branch left or right
number tree leaves must be at least number of possible inputs = n!
after t comparisons, at most 2t tree leaves
so for m = n! tree leaves we need at least lg (n!) comparisons
lg (n!) ∈ Θ(n lg n)
so any comparison-based sort of n keys takes Ω(n lg n) time
can we comparison-sort 6 keys with at most 9 key comparisons?
no 6!= 720, and 29 = 512 < 720, so lg 720 > 9