

|
PCP News
Definition:
† Given an alphabet S, one instance
of Post's
correspondence problem of size s is a finite
set of pairs of strings (gi
, hi) ( i = 1...s
s>=1) over the alphabet S.† A solution of length n >= 1 to this instance is a sequence
i1 i2 ... in of selections such that
the strings gi1gi2
... gin and hi1hi2
... hin formed by concatenation are identical. Width of a PCP instance is the length of the longest string in gi and hi (i = 1, 2, ... , s). Pair i is the short name for pair (gi , hi), where gi and hi are the top string and bottom string of the pair respectively. Mostly, people are interested in optimal solution, which has the shortest length over all possible solutions to an instance. The corresponding length is called optimal length. We use the word hard or difficult to describe instances whose optimal lengths are very large. For simplicity, we restrict the alphabet S to {0, 1}, and it is easy to transform other alphabets to their equivalent binary format. To describe subclasses of Postís Correspondence Problem, we use PCP[s] to represent the set of all PCP instances of size s, and PCP[s, w] the set of all PCP instances of size s and width w. For convenience, we use a matrix of 2 rows and s columns to represent instances of PCP[s], where string gi is located at (i , 1) and hi at (i , 2).
The following is the matrix representation of the instance {{100, 1}, {0, 100}, {1, 00}} in PCP[3,3].
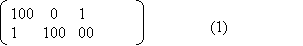 Let's consider the result of selections of pair 1, 3, 1, 1, 3, 2, 2 accordingly. They can be shown in the following table with each selection assigned a different color:
After the elimination of blanks and concatenation of strings in the top and bottom separately, it turns to: 1001100100100
Now, the string in the top is identical to the one in the bottom; therefore, these selections form a solution
to PCP (1). When all combinations of up to 7 selections of pairs are tested, this solution is thus proven to be the
unique optimal solution to this instance.
You are the No.
Last modified on April 25, 2003 by Ling Zhao |
Introduction
Solving hard PCP instances
Instances having no solutions
Hard instances list
Documents
Next step
Contact |
||||||||||