Actuation Subspace Prediction with Neural Householder Transforms
MSc Thesis in Computing Science by Kerrick Johnstonbaugh
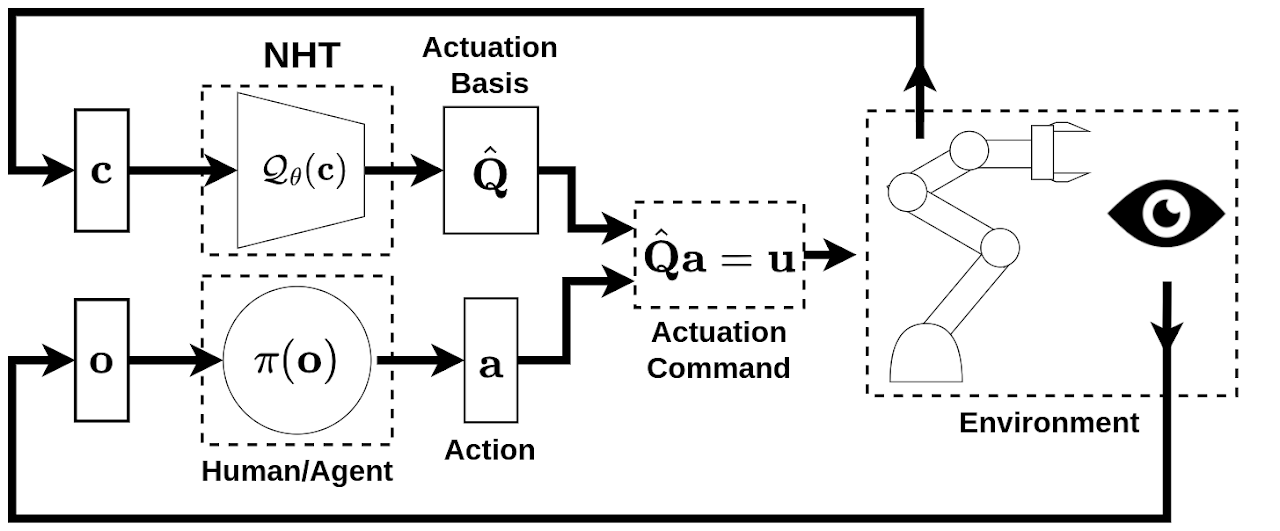
A pre-trained NHT model can be used to enable control of high-dimensional robotic manipulators with a low-dimensional interface.
Abstract
Choosing an appropriate action representation is an integral part of solving robotic manipulation problems. Published approaches include latent action models, which train context-conditioned neural networks to map low-dimensional latent actions to high-dimensional actuation commands. Such models can have a large number of parameters, and can be difficult to interpret from a user perspective. In this thesis, we propose that similar performance gains in robotics tasks can be achieved by restructuring the neural network to map observations to a basis for context-dependent linear actuation subspaces. This results in an action interface wherein a user's actions determine a linear combination of state-conditioned actuation basis vectors. We introduce the Neural Householder Transform (NHT) as a method for computing this basis.
This thesis describes the development of NHT from computing an unconstrained basis for a state-conditioned linear map (SCL) to computing an orthonormal basis that changes smoothly with respect to the input context. Two teleoperation user studies indicated that SCL has increased completion rates and user preference compared to latent action models. In addition, simulation results show that reinforcement learning agents trained with NHT in kinematic manipulation and locomotion environments tend to be more robust to hyperparameter choice and achieve higher final success rates compared to agents trained with alternative action representations.
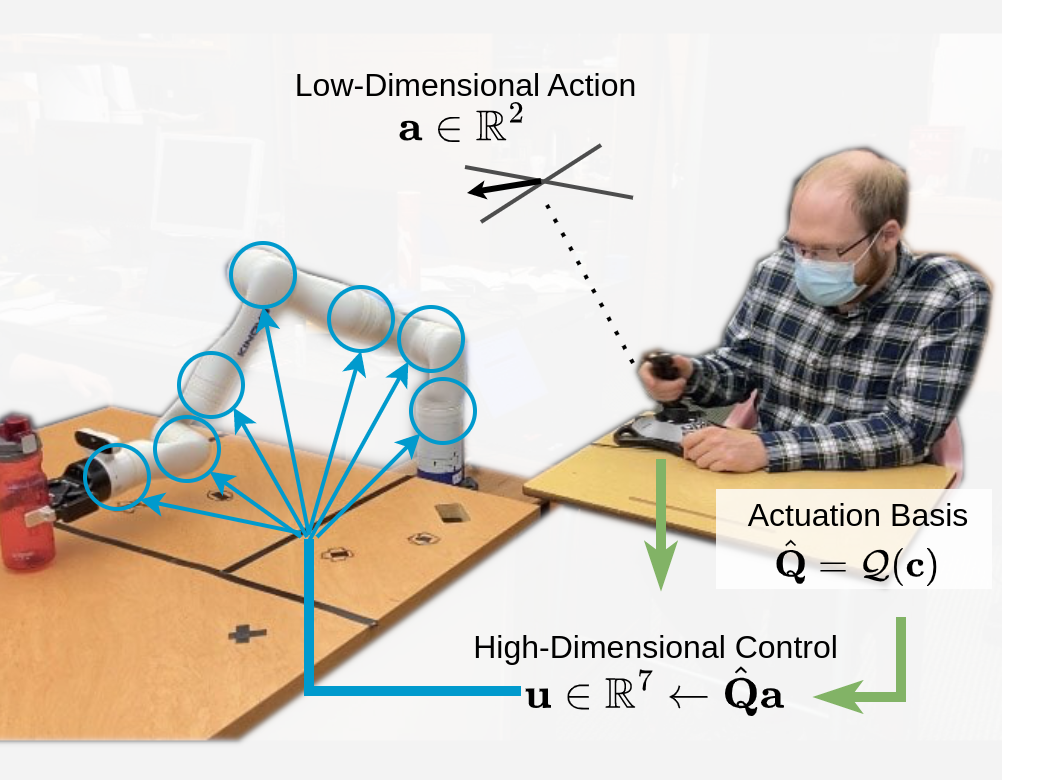
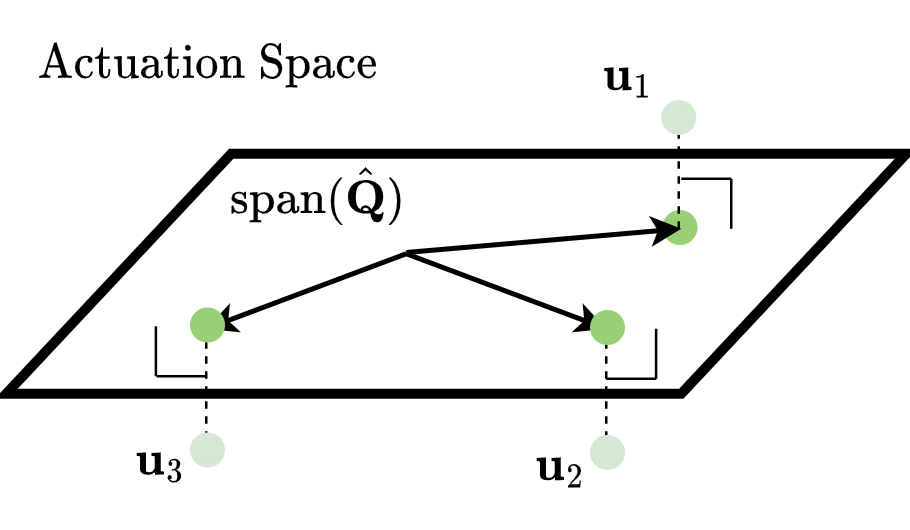
Illustration of a 2D actuation subspace.
The actuation vectors u exist in a higher-dimensional vector space. NHT learns a lower-dimensional actuation subspace that lies close to the observed actuation commands.
What is an actuation subspace?
Actuation is a generic term for causing a machine or device to operate. In this thesis we deal with both joint velocity commands and joint torque commands. We use the term actuation to refer to either.
As we are primarily focused on robotic manipulation tasks, these actuation commands typically take the form of seven-dimensional vectors. Each element of the actuation command vector u corresponds to a joint torque or velocity command for one of the seven motors in the robot.
Control of systems with 7+ degrees-of-freedom typically requires complex and/or expensive control interfaces. We seek to enable control of these systems with simple two-axis joystick interfaces by identifying context-dependent actuation subspaces.
A linear subspace is a vector space that is a subset of some larger vector space. In this case the larger vector space is the actuation space, the set of all n-dimensional vectors, where n is the number of motors in the robot. To enable control with a two-axis joystick, we learn a 2-dimensional subspace that lies close to the actuation commands observed in demonstrations of the task.
Neural Householder Transform
A single (global) linear actuation subspace is often insufficient to describe the actuation commands involved in a non-trivial manipulation task. For this reason prior work has investigated using neural networks to learn context-dependent non-linear functions from low-dimensional actions to high-dimensional actuation commands [1].
We build on this prior work by using neural networks to learn context-dependent linear mappings.
Simply put, our neural householder transform (NHT) learns to compute a basis for the actuation subspace most appropriate to the current context.
The actuation bases computed by NHT are guaranteed to be orthonormal, and we prove that the basis changes smoothly with respect to changes in context. To achieve these properties, NHT relies on Householder reflections, a technique commonly used to compute the matrix QR decomposition [2].
Please see chapter 4 sections 2-3 of the thesis for details on the computation performed by NHT.
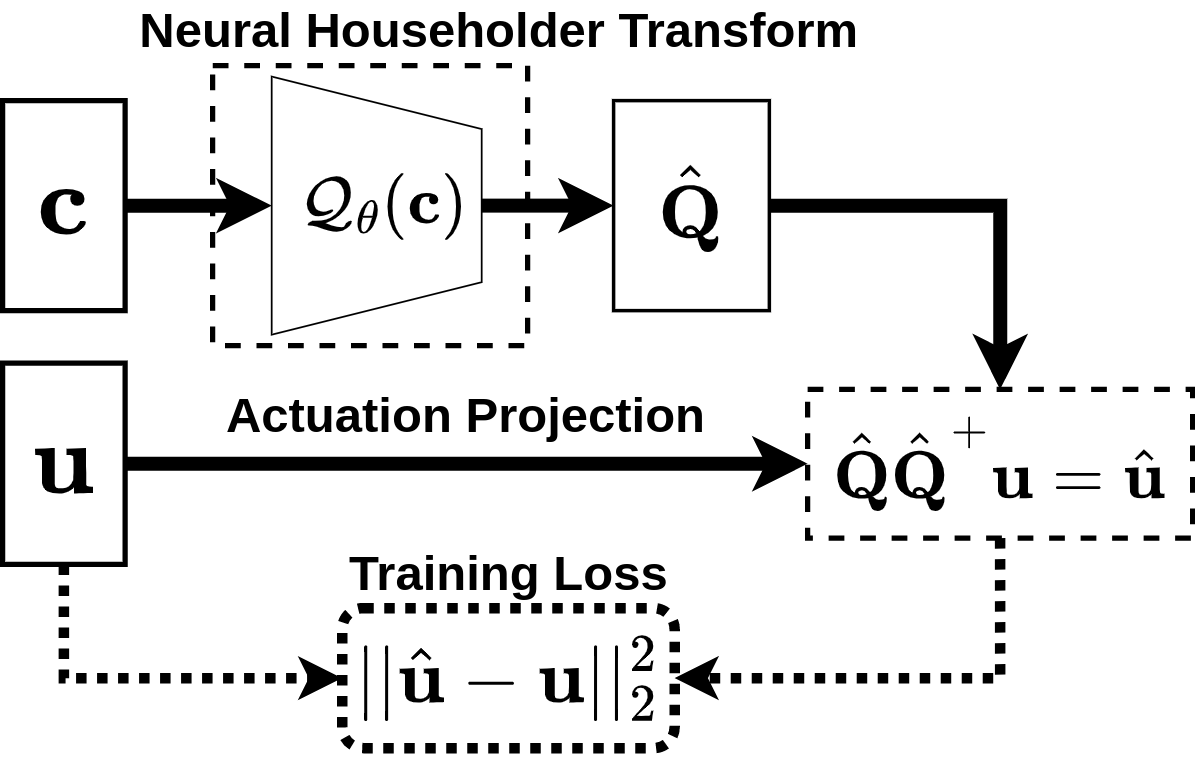
Offline training procedure for NHT. Task-specific actuation commands u (high-dimensional joint velocities or torques) and the context c of those commands are used to train NHT.
WAM Manipulation RL Environments
The University of Alberta Vision and Robotics Lab has 3 cable driven Barrett WAM robots. To facilitate reinforcement learning research on these platforms, we developed two constrained kinematic manipulation environments with a simulated 7-DoF WAM. These RL environments use the OpenAI gym API, and thus should be easy to use for any researcher familiar with this API. The environments were designed to highlight the potential for NHT to enable safe exploration in manipulation tasks with safety concerns or other constraints (e.g. prevent manipulator from generating excessive force by pushing hard into a solid table).

WAMWipe
In WAMWipe the goal is to control the manipulator such that the flat face of the last link remains flush against a table while sliding to a randomly sampled goal position. While the end-effector remains constrained to the plane of the table, the nonlinear kinematics of the robot make this problem impossible to solve with a single 2D actuation subspace. Solving the task requires the ability to adapt the actuation subspace based on the current context.
The reward is -1 every step unless the end-effector is within a small distance of the goal position, in which case the reward is 0. Episode failure occurs if the end-effector: (1) Pushes into the table, (2) Lifts off of the table, or (3) The end-effector tilts such that it is no longer flush with the table.
WAMGrasp
Certain objects can only be grasped from specific orientations. In WAMGrasp the goal is to simultaneously reach a randomly sampled grasp-point, while achieving a goal orientation. The reward in WAMGrasp is -1 at every step unless the end-effector is within a small distance of the grasp-point with a satisfactory orientation. Episode failure occurs if the end-effector collides with either the object being grasped (large red sphere in gif on the right) or the table.

Reinforcement Learning with NHT - Results
We trained NHT to perform actuation subspace prediction for the WAMWipe and WAMGrasp tasks, and then trained RL agents that acted in the lower-dimensional actuation subspaces. We compared this approach to two other approaches to reduce the dimensionality of the action space: SVD and LASER.
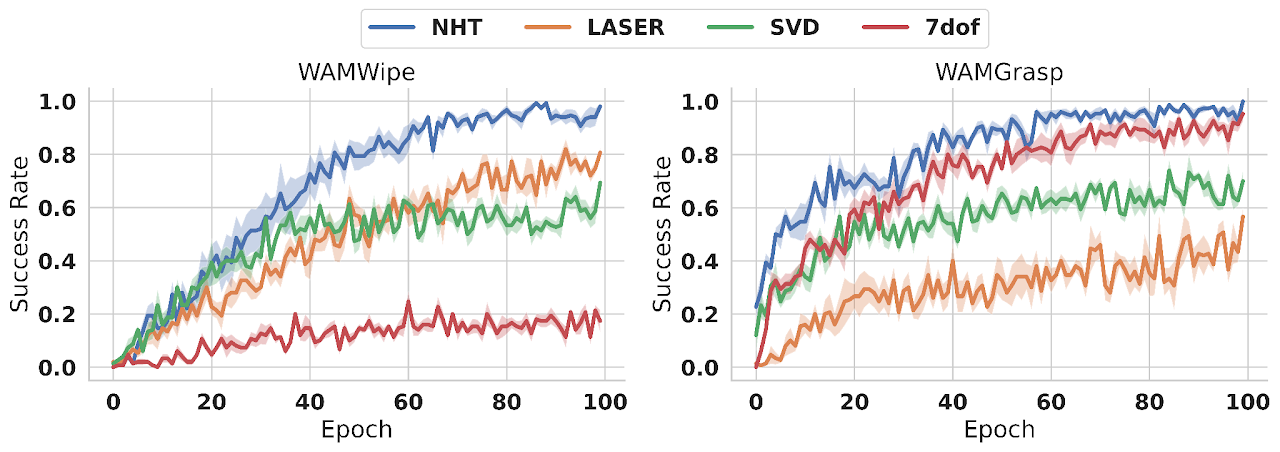
Learning curves from the best-performing agents in our hyperparameter search experiment.
To ensure a fair comparison between NHT and the baselines, we performed extensive hyperparameter search experiments. Please see chapter 6 section 3 of the thesis for the details of this experiment.
The learning curves of the best performing NHT, LASER, SVD and 7-DoF agents are shown above.
The distributions of agent performances from this experiment (all hyperparameter configurations) are shown in the violin plots to the right. Higher is better.
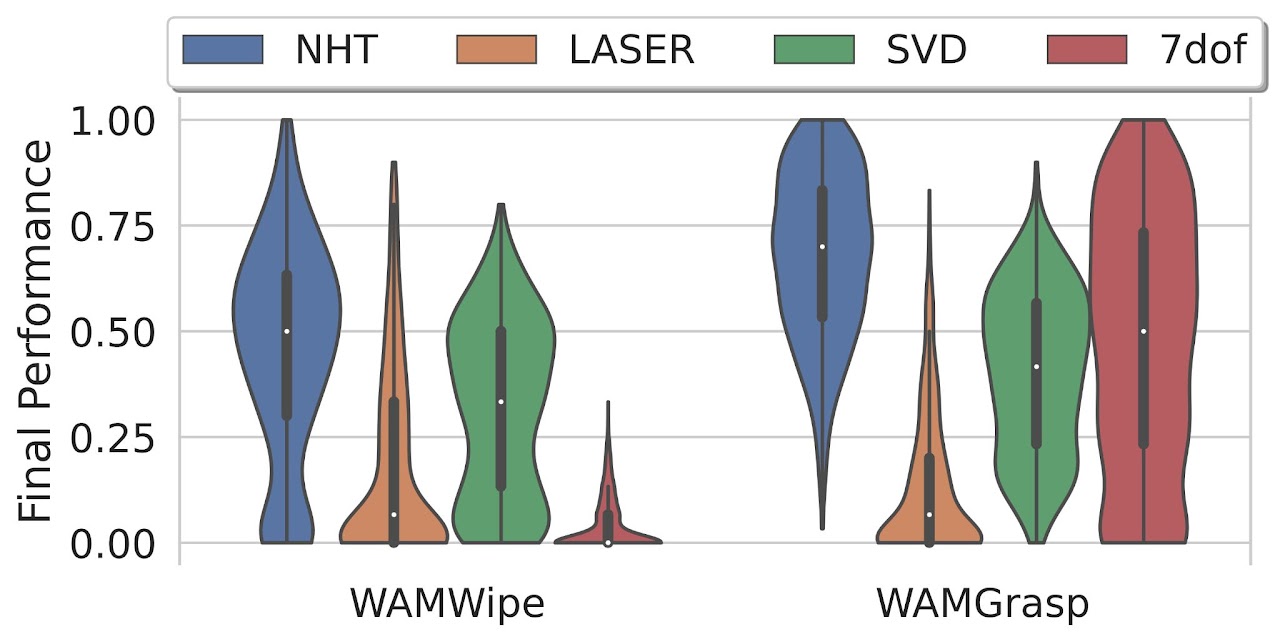
Violin plots of final agent performances from hyperparameter search experiments in WAM RL environments.
User Studies with State Conditioned Linear Maps
Our first approach to actuation subspace prediction was called State Conditioned Linear (SCL) maps. Like NHT, SCL learns a function that maps the current context to an appropriate actuation basis. We performed two user studies in which participants used SCL to control a 7-DoF manipulator.

Pouring with SCL
In our pouring user study, we compared SCL for teleoperation to (1) mode switching (2) a conditional autoencoder baseline from the literature [1].

Percentage of successful trials with Mode Switching, Conditional Autoencoder, and SCL control interfaces.

Likert scale for user opinions of the different control interfaces.
[1] D. P. Losey, K. Srinivasan, A. Mandlekar, A. Garg, and D. Sadigh, “Controlling Assistive Robots with Learned Latent Actions,” 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020. doi: 10.1109/ICRA40945.2020.9197197.
[2] M. Heath, Scientific Computing: An Introductory Survey, Revised Second Edition, ser. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics, 2018, isbn: 9781611975574. [Online]. Available: https://books.google.ca/books?id=faZ8DwAAQBAJ.
