Introduction to Compilers

Due 23:59, Sunday, March 11, 2001

Objective

This assignment introduces the translation of a programming language source code into executable form. It also introduces you to the reality of programming. You must take an existing program, read it and understand it, and then add new capabilities to it by modifying the existing code.

The key to successfully completing this assignment is to understand the program you are modifying, especially the principles behind its design. The actual programs are not too complicated, and the required modifications are fairly easy to do.

Notes

• WARNING: Your Makefile must be designed so that make all produces all of the required executables for this assignment. If it does not bad things will happen. In particular, your assignment will not be marked!

• Collaboration is not allowed for this assignment, that is, each of you must do the task on your own. Obviously you can, and even should, DISCUSS the assignment and its possible solutions with others in your lab section, but you must write your own solutions. We assume that you are aware of the Regulations undergraduates should know, as stated in Undergraduate Laboratories WWW Server.

• There are many details that must be handled for you to receive full marks on this assignment. You should pay attention to these details. The Makefile must correctly produce all the programs required, and each function/procedure and program file must be correctly named and must behave in the appropriate way. If the details aren't addressed successfully you will lose marks.

• No action is necessary to submit your assignment. Your work will be automatically extracted from your CVS repository on the due date and time. We will also be extracting from your repository at times prior to the due date in order to monitor your progress toward the final submission. Questions about these exercises will be answered in the course newsgroup. You are expected to check that newsgroup regularly, so that you are fully informed.

Background Information

A compiler translates a program written in one language (like C) into another language (like Intel assembler) for high-speed execution on a specific computer type. An interpreter takes a program written in a language (like Perl) and converts it into a machine-independent pseudo-code that can execute more slowly, but directly on many machines.

Both compilation and interpretation require parsing the input language. Parsing takes the stream of characters that represents the program text and builds an internal data structure, called a parse tree, that represents the syntactic structure of the program. Once the parse tree has been built, it can be traversed to produce a translation of the program (as for a compiler) or executed (as for an interpreter).

Parsing usually proceeds in two phases: lexical and grammatical.

The lexical phase:

In the lexical phase the characters in the input stream are processed into larger chunks called tokens. Comments are usually thrown away, keywords and operators are identified (like do, for, +, *), and constants (like numbers 3.1415 and strings "Hello") and identifiers (like fred, malloc) are extracted. The idea is that each important piece of syntax becomes a token. Thus the input stream of characters becomes an input stream of tokens which, being single units, are much easier for a program to process. Each token is a bit of syntax, like nouns and verbs in sentences.

The grammatical phase:

In the grammatical phase, the stream of tokens is parsed according to the grammatical rules of the programming language. These grammatical rules form the grammar of the language.

Grammars are usually written as a set of rules. The rules are equations formed by having a grammar variable on the left, the := operator in between, and an expression involving grammar variables and tokens on the right. Grammar variables are usually written with angle brackets (<, >) around them. Tokens are usually written as names (like ID) or a symbol in single quotes, like ( ';'). For example here is a rule:

that states that <SENTENCE> consists of a NOUN followed by a VERB followed by an OBJECT followed by a period.

The rule says that any four tokens that satisfy the right hand side of the rule can be taken as a syntactically correct sentence. Here is another rule:

that states that <SENTENCE> consists of a NOUN followed by a VERB followed by a period. In other words there a two ways of forming a syntactically correct sentence.

It is very common for there to be many ways to compose a sentence, and we often write the rules together, with the right hand sides separated by a vertical bar ( | ), which is read as 'or'. For example:

This rule can be read as "a sentence is composed of a noun verb object period or a noun verb period."

Here is a grammar for fully parenthesized arithmetic plus-times expressions:

The result of parsing a program is a parse tree representing a syntactically correct program. Once you have the parse tree you can then do things that add semantics (that is, meaning) to the program.

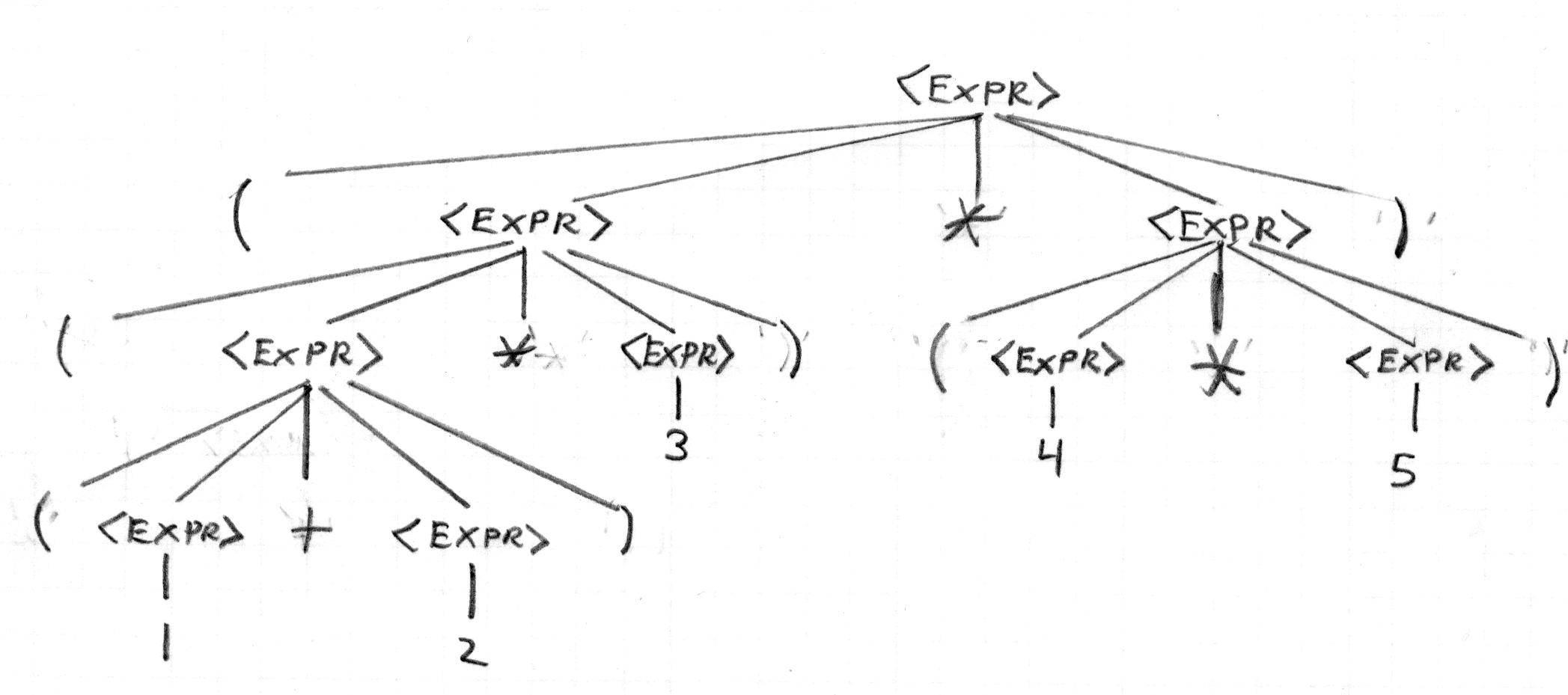
The parse tree for this expression:

according to the grammar above would be:

The structure of the parse tree and the rules of the grammar are related. Each internal node in the parse tree corresponds to an instance of the <EXPR> variable on the left hand side of a rule, and the immediate children correspond to the tokens and variables on the right hand side of the rule. Leaves of the tree are always tokens, internal nodes of the tree are always variables. In fact, an inorder traversal of the tree, ignoring all internal nodes and just keeping the leaves, will generate the original sequence of tokens that were parsed.

How did we obtain the parse tree? The kind of grammars we are using here are called context-free. Loosely speaking, this means is that it is possible to parse pieces of the input independently of the tokens that precede or follow it (the context). That is, the rules of the grammar do not change depending on where the parser is in the stream of input tokens. The net result of this is that context-free languages are quite easy to parse.

The parser technique that we use here is called recursive descent. The basic idea is to give the parser the task of parsing a particular rule defined by the variable on the left-hand side. For example, we might tell it to look for an <EXPR>. It then selects, in order, each of the possible right-hand sides of the rule for processing.

Processing a rule means to expand the right hand side, and look for each of the individual pieces. For example the rule

expands into the task of matching CONSTANT to the next input tokens. Since CONSTANT is itself a token, this means simply checking that the next token in the input stream is of type CONSTANT. If so, the rule succeeds, and the search for an <EXPR> is finished.

If the next token is not a CONSTANT, then this rule fails, and the next one is tried, in this case the rule

The right-hand side is expanded, and the next token is checked to see if it is a '('. If not the parse fails, and the next rule is tried. If the token is a '(', a simple token match is not possible, since the next piece of the rule is a variable, <EXPR>. Instead a recursive call is made to the parser to look for an <EXPR> (the recursive descent). If an expression is found, then the next token to be matched should be a '+'. This process continues until either the rule succeeds, or fails.

If none of the rules work, the parse of <EXPR> fails, and failure is returned to the initiator of the parse. On success, the resulting parse tree is returned to the initiator of the parse for inclusion into the tree that the initiator is itself building.

The overall parse starts with some variable that represents a valid complete input, such as <PROGRAM> in the Etran grammar, and is successful if all of the input tokens are completely matched. The initial parser that we give you is instrumented to display the rules being tried as the parse proceeds so that you can get a more dynamic understanding of the parsing process.

Assignment Tasks

In the directory ~c201/public/ass2 there is a collection of files that form a simple "compiler" for a language of arithmetic expressions that we call Etran. You should begin by creating your CVS directory and placing these files into it. Then do a make etran-s to compile and build the sample compiler, called etran-s, that reads an Etran program and prints it out. Note, Etran programs all end in file extension .etran.

Once you have a working compiler then you need to study it and try experiments on it to build an understanding of how it works. We will also be going over the operation of the compiler in class. Take advantage of the DEBUG settings in the compiler.

The Etran language of this assignment has programs that look like this:

That is, a sequence of statements (ended by ';') where each statement is either an assignment or an expression. The full grammar for Etran is in the files associated with the assignment.

Once you understand what the program is doing, then you are ready to begin the following "enhancements". Note that you may not want to do them in the order presented, since not every modification depends on doing the previous one. You are asked to create three programs: etran-c, etran-v, and etran-hp.

1. For simplicity, the token allocator in lexical.c uses a fixed length array that can be overflowed by a long program. Improve the token allocator so that it can handle arbitrarily large input programs. The program etran-v will be tested for this capability.

2. Improve the syntax diagnostics to give the line number and token at which the parser gave up. For example, if the second line of a program contained the statement
   b = (2*a;

   the compiler would generate an error message along the lines of Syntax error on line 2, near "a;"

   The program etran-v will be tested for this capability.

3. Add the division / and subtraction - arithmetic operations to the grammar so that expressions involving all four of the standard operations are allowed. All programs will be tested for this capability.

4. etran-c: Using the unparse function in etran-s as a pattern, build a program called etran-c that evaluates each statement in the Etran program and prints out its computed value. Do not worry about expressions that have variables in them, either take 0 as the value of a variable, or generate a message at evaluation time.

   For example, with this Etran program

   10+3*5;

   ( 20 / 2 ) * 3;

   a = 40-2;

   etran-c would generate output:

   25;

   30;

   a = 38;

5. etran-v: Add a symbol table to etran-c so that the assignment statements actually store values into the variables, and the current value of a variable is used inside an expression. With the symbol table in place, expressions can actually use variables. Call this new program etran-v

   A symbol table is simply a data structure that stores <name,value> pairs in a way that you can look up a name and get or set its value. A very simple symbol table is just an array of structures, where one element is a string of characters representing the name of an identifier, and the other a double-precision number corresponding to its value.

   For example, with this Etran program,

   a = 3;

   b = ( a + 2 ) * a; b / a;

   etran-v would output:

   a = 3;

   b = 15;

   5;

6. etran-hp: Instead of evaluating the expressions, generate code for a reverse polish stack machine with instructions like an HP calculator. The following table gives all the possible instructions. Let x be the top of the stack, and y the location just below it.

   push(constant)	push a constant onto the stack
   pop	pop the top element off the stack
   rcl(variable)	push the value of variable onto the stack
   sto(variable)	copy the top of the stack into variable
   +	replace x, y on the stack by x+y
   *	replace x, y on the stack by x*y
   -	replace x, y on the stack by y-x
   /	replace x, y on the stack by y/x

   Call this new program etran-hp

   Thus etran-hp would convert the following Etran program:

   a = 3 * 4 -2;

   b = ( a + 2 ) * a;

   a / b;

   into something like:

   push(3) push(4) * push(2) - sto(a) pop

   rcl(a) push(2) + rcl(a) * sto(b) pop

   rcl(a) rcl(b) / pop

   Just so you are clear on what a syntactically correct stack machine program is, the grammar for the stack machine instructions is as follows:

   <STACKPROG> :=	<INST-LIST>
   <INST-LIST> :=	<INST>	|
   	<INST> <INST-LIST>
   <INST> :=	'pop'	|
   	'+'	|
   	'*'	|
   	'-'	|
   	'/'	|
   	'push' <CONST-ARG>	|
   	'rcl' <VAR-ARG>	|
   	'sto' <VAR-ARG>
   <CONST-ARG> :=	'(' CONSTANT ')'
   <VAR-ARG> :=	'(' ID ')'

   where CONSTANT is any decimal number, and ID is any identifier acceptable to Etran. All tokens must be surrounded by whitespace (blank, tab, newline), except the parentheses for arguments. Parentheses need not have whitespace inside them, and the opening parenthesis does not need white space before it.

IMPORTANT NOTE ON NAMING CONVENTIONS:

Within your ass2 directory, you should have 3 new main programs, etran-c.c, etran-v.c, and etran-hp.c that implement the main requirements we asked for. Ideally, all the changes you make to lexical.c, lexical.h, parse.c, and parse.h are usable by every version of etran. Even etran-s, although it would be incomplete, since it doesn't understand the - and / operations.

However, as a form of risk management, you may not want to do all your changes at once. So nothing prevents you from naming various versions of the lexical scanning and parsing modules to reflect this. For example, you might want to do etran-c using the original version of lexical.c because you didn't have your fancy token allocator ready. So make a copy of the original, call it lexical-c.c and then include that into etran-c.c. You might also want to have a lexical-c.h.

JUST MAKE SURE YOUR Makefile DOES THE RIGHT THING AND YOU REALLY INCLUDE THE HEADERS YOU INTEND. We will be printing everything that is in your CVS directory, except the readln and logger modules.

Marking Scheme

Marking will be primarily based on correct capabilities. Marks will then be reduced for inadequate documentation. The key thing to remember is that you should be documenting all the changes you made to the original code, plus adding any additional documentation you feel is necessary.

The assignment has 45 total marks, broken down as follows:

Capability marks:

1. (2 marks) Improved Token Allocator (tested on etran-v)
   • should not die on a reasonable test case
   • inspect code to see if dynamic allocation is being used

2. (8 marks total) Improved Syntax Diagnostics (tested on etran-v)
   • (3 marks) indicate at which line number the parse gave up
   • (3 marks) indicate at which token the parse gave up
   • (2 marks) overall strategy for error diagnostics and precision of the error message

3. (20 marks total) Add / and - operators. (tested on all)
   • (6 marks) add - operator
   • (6) marks add / operator
   • (5 marks) get left associativity correct. That is, 1-2-3-4 should be parsed as (((1-2)-3)-4) and 1/2/3/4 should be parsed as (((1/2)/3)/4)
   • (3 marks) allow +/- sign on constants

4. (5 marks) etran-c simple calculator
   • what happens with divide by 0 and other numerical disasters like overflow?
   • does it compute the test results properly

5. (5 marks) etran-v calculator with variables
   • does fetch and store into variables work?
   • output should distinguish between simple expression evaluation and assignment to a variable, as per the example
   • does it compute the test results properly

6. (5 marks) etran-hp code generator
   • does it properly convert the test expression into the hp instruction stream.

Documentation marks:

Up to 50% of the total available marks on any one section can be deducted (not exceeding the mark earned in the section) for poor documentation, not making assumptions clear, poor coding style, excessively bizarre solutions, etc. So it is possible to have a correct program, but lose half of your marks.

Deliverables

• You must create a CVS repository for your assignment. Lab 1 shows you how to do this. Your repository must contain a directory called ass2. In this directory, you must commit all necessary .c and .h files, along with your Makefile. Do not commit any other files (core files, backup files, etc.) or you will lose marks.

• Your Makefile must have entries in it for each part of this assignment. Each part must be named as described above. Your Makefile must be designed so that a make all compiles all parts of this assignment.

• Your code should compile without any warning messages when using the flags -Wall -ansi, otherwise marks will be deducted. Your Makefile should include these flags.

• Make sure that all your debugging information is turned OFF and that the programs generate only the specified output. That is, if there are no errors in the input, the output should look like the examples above. If there are errors in the input, then you can generate an appropriate message.

• Please make sure that every file (including your Makefile) you submit contains a banner with the following information: /*-----------------------------------------------------------------------
# Student's Name:
# Student's ID:
# Student's Unix Login:
# Assignment
# Lab Section:
# TA's Name: (for the lab group above)
# CMPUT 201, Class Section:
# Instructor's Name: (for section above)
*-----------------------------------------------------------------------*/

Revision Information

Contact Tony Marsland, tony@cs.ualberta.ca, about problems with or suggestions about this document.

Copyright © 2000, University of Alberta. This document was produced using the Apalon mark-up language, developed by the Software Engineering Research Lab, Dept. of Computing Science, U of A. Apalon is implemented in Perl, http://www.perl.com. Every computing scientist should know Perl.