Homework #3 -- Cmput651 (Fall 2008)

Due: 11:59pm, Friday, Dec. 5, 2008

Total points: 65

Refer to the web page for policies regarding collaboration, due dates, and extensions.

1. Particle-Based Approximate Inference #1
   [15 points] (programming)
   Implement likelihood weighting on the elaborate model of recommendation from subquestions C and D in Homework #2's Part 4 (Clique Trees). Use the same conditional probability tables and parameter values. Answer the same queries as before in subquestion D using different numbers of samples: 10, 100, 1000, 10000, and 100000 samples.

   ---

2. Particle-Based Approximate Inference #2
   (KF Exercise 11.10) Regular Markov chains
   [20 points]

   Consider the following two conditions on a Markov chain T:

   1. It is possible to get from any state to any state using a positive probability path in the state graph.
   2. For each state x, there is a positive probability of transitioning directly from x to x (a self-loop).

   Answer the following questions:

   1. Show that, for a finite-state Markov chain, these two conditions together imply that T is regular.
   2. Show that regularity of the Markov chain implies condition 1.
   3. Show an example of a regular Markov chain that does not satisfy condition 2 (with a short explanation of why this is such an example).
   4. Now let's weaken condition 2, and require only that there exists some state x with a positive probability of transitioning directly from x to x. Show that this weaker condition and condition 1 together still suffice to ensure regularity.

---

3. Learning Undirected Models #1
   [10 points]
   (KF Exercise 19.1)
   
   
   
   
   
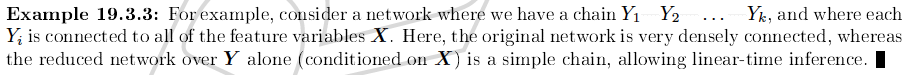
   Note. You should assume the following:
   1. All X's and Y's are discrete, binary variables.
   2. All factors (for the original, unconditioned Markov network) are clique factors (pairwise factors).
      I.e. don't use (non-reduced) factors with a single variable in their scope.
   3. All factors &phi_a,b(Y_i, Y_j) or &phi_a,b(Y_i, X_j) are indicator functions.
      For example, for the clique {Y₁, X₁}, we will have four indicator functions:
      • &phi_0,0(Y₁, X₁) = Indicator(Y₁=0, X₁=0)
      • &phi_0,1(Y₁, X₁) = Indicator(Y₁=0, X₁=1)
      • &phi_1,0(Y₁, X₁) = Indicator(Y₁=1, X₁=0)
      • &phi_1,1(Y₁, X₁) = Indicator(Y₁=1, X₁=1)
      In this case, the parameter vector &theta_1,1^xy (sorry about the clumsy formatting) will be
      a length four vector with one element for each of the above indicator functions.
   
   Hint: Use Koller-Friedman equation 19.7 (gradient for log conditional likelihood).

---

4. Learning Undirected Models #2
   [10 points]
   KF Exercise 19.12:
   Let H* be a Markov network where the maximum degree of a node is d*. Show that if we have an infinitely large data set D generated from H* (so that independence tests are evaluated perfectly), then the Build-Skeleton procedure of Figure 3.17 (reproduced below) reconstructs the correct Markov structure H*.
   
   
   Koller-Friedman Figure 3.17:
   Algorithm for recovering undirected skeleton given a distribution
   
   

---

5. Inference in Hybrid Networks #1
   [10 points]
   (KF Hybrid Networks chapter handout, Exercise 13.1)
   Let X and Y be two sets of continuous variables, with |X|= n and |Y| = m.
   Let p( Y | X) = N(Y;a +BX, C) where a is a vector of dimension m, B is an m × n matrix, and C is an m × m variance-covariance matrix. This dependence is a multi-dimensional generalization of a linear Gaussian CPD. Show how p(Y| X) can be represented as a canonical form.
   

   ---

6. Inference in Hybrid Networks #2
   Dropped from assignment (topic not covered in lecture due to time constraints).