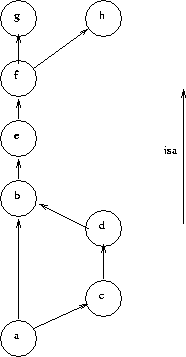
object(a). object(b). object(c). object(d). object(e). object(f). object(g). object(h). isa(a,c). isa(c,d). isa(d,b). isa(a,b). isa(b,e). isa(e,f). isa(f,g). isa(f,h).
You should submit one file containing all your programs along with documentation. (Include answers to dry-lab questions as comments.) Your programs will be run against our solutions to provide feedback to your work. You may submit many versions; the last one before the deadline will be retained as your submission. (If you submit prior to the deadline, but plan to use one or two of your excused late days, you must tell the TAs to disregard your pre-deadline submission... or risk their wrath.) Questions about the try command can be directed to tommy@cs.ualberta.ca
Assignment Marks: There are a total of 75 points possible on this assignment. It is worth 8% of the total course grade. Your programs must be readable and understandable as well as correct. You could lose up to 1/2 of the marks for bad style even if your programs are correct. See DocumentationGuidelines, TA'sGuidelines and programming style and marking guideline for an overview of the documentation, testing examples, etc. that we expect.
In general, your Prolog function may involve more than one clause, and
may also involve new predicates.
You should also make sure you code is reasonably efficient -- or at
least not incredibly inefficient.
As always, no line should be longer than 80 characters.
Define the double_me( X, Y ) relation that holds when Y is a list structure that contains the same basic structure, and elements, that appeared in X, but each entry in Y is a list containing two copies of the entry in X. Hence,
|?- double_me( [a, b, [c,d]], Y). Y = [ [a,a], [b,b], [[c,d], [c,d]] ] ? ; no |?- double_me( [1, X], [Y, [2, Q]]). Q = 2, X = 2, Y = [1,1] ? ; no |?- double_me( [1, X], [Y, [2, 3]]). noIn general, your program should work even even if there are variables in either argument -- as suggested by the above examples. Be sure to specify if that is not true.
You should also discuss what the program will do if the inputs are not standard lists, etc.
Define the flatten( X, Y ) relation that
holds when Y is a list structure that contains the same elements as X,
in the same order, but as a list.
Hence,
|?- flatten( [a, b, [c,d]], Y). Y = [ a, b, c, d] ? ; no |?- flatten( [a,[b],[[[c]]], [d,e]], X). X = [a,b,c,d,e] ? ; noYou may use the code
non_nil_atom(X) :- X \== [ ], atom(X).to test if a component is an atom that is not [ ]. You may assume that this will "catch" the base case.
(The comments written for #1, about variables and error conditions, apply here as well.)
| Structure | Representation |
|---|---|
 |
object(a). object(b). object(c). object(d). object(e). object(f). object(g). object(h). isa(a,c). isa(c,d). isa(d,b). isa(a,b). isa(b,e). isa(e,f). isa(f,g). isa(f,h). |
We assume that the inheritance structure is a directed acyclic graph (DAG). While it will not have cycles, there may still be multiple paths connecting a pair of nodes. In the example above, we can get from a to b via either a->b or a->c->c->d->b.
Write a relation bft(X,Y) that holds when Y is an ancestor of X in the isa-based inheritance structure. If Y is not instantiated, then successive values for Y should be produced in a breadth-first order. You should produce each ancestor exactly once; no duplicates.
Using the structure shown above, bft(a,X) should return:
| ?- bft(a,X). X = a ? ; X = c ? ; X = b ? ; X = d ? ; X = e ? ; X = f ? ; X = g ? ; X = h ? ; noThe results should be in exactly this order. For instance, even though we can reach both c and b directly from a, we choose to start with c, because the statement isa(a,c) comes before the rule isa(a,b) in the Prolog database.
bft(a,b) should return yes, as should bft(a,h).
bft(b,a) and bft(f,c) should return no.
For the purposes of this question, the predicate findall/3 may be useful. It is used as follows:
| ?- findall(A, bft(a,A), X). X = [a,c,b,d,e,f,g,h] ?In this case findall/3 generates a list of all A that satisfy the relation bft(a,A), in the order they would be produced by standard Prolog backtracking.
Warning: While you may want to (and, in fact, should!) use your own objects and isa statements when testing your code, make sure to comment them out of your code before you submit. Otherwise, these statements may add structure to the hierarchy, which may cause your system to fail try's tests. If this happens, you will be penalized.
The following set of rules specify the components of a boolean circuit:
and_gate(X) holds when X is an and-gate(Note the latter 2 are terms, and not predicates. Hence, the proposition connected( output(a9, 1), input(x10, 2) ) means the first output of the device a9 is connected to the 2nd input of device x10. Also, value( output(a9, 1), 1) means the value of the the first output of the device a9 is 1.)
or_gate(X) holds when X is an or-gate
xor_gate(X) holds when X is an xor-gate
not_gate(X) holds when X is an not-gateconnected( P1, P2) holds when the port P1 is connected to the port P2
value( Port, V) holds when the value of the port Port is V
input(X, Pj) designates the j-th input port of the gate, X
output(X, Pj) designates the j-th output port of the gate, X
PartA (10marks) Write down the rules that state
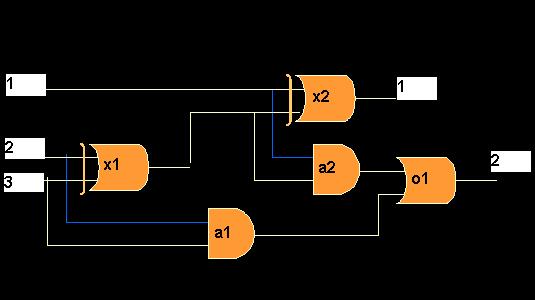 .
.
Write down the axioms that specify this device, called full_adder.
You should use the names on the figure: a1, a2, x1, x2, o1.
Note that full_adder has 3 input ports (the two bits to add, and a carry
bit in) and 2 output ports (for the resulting value, and the carry bit
out).
Use this description to compute what the output will be, for various
different sets of input triples
--- eg, when the input is <1, 0, 1>, as represented by the
facts
value(input(full_adder, 1), 1) .
value(input(full_adder, 2), 0) .
value(input(full_adder, 3), 1) .
Note: you may want to use a single rule for each type of gate (eg, one rule for and-gates, another for or-gates, ...) and have a set of facts that succinctly describe the i/o behavior of correctly working and-gates, another set of facts describing the i/o behavior of correctly working or-gates, etc.
PartC (10marks)
Of course, this description assumed that the gates were all working
correctly --
eg, an "ok" and-gate maps <1,1> to 1.
Add the new relation
state(X, S) which holds when gate X is in state S, where S can be