Quantum
Computing for Computer Scientists
CMPUT 604 B1
Winter 2019
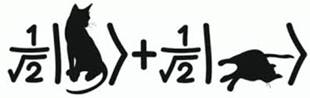
|
Instructor: Pierre Boulanger Office hours: after class or by
appointment Course will be every Friday
in CSC 2-49 from 16h15 to 18h15 Prerequisites: Students
should be comfortable with linear algebra concepts such as unitary and
Hermitian matrices. They should also have basic knowledge of probability
theory. Prior knowledge of quantum mechanics is helpful but not
required. Course Description: This
course is an introduction to theory and applications of quantum information
and quantum computation, from the perspective of computer science. The course
will cover classical information theory, compression of quantum information,
quantum entanglement, efficient quantum algorithms, quantum error-correcting
codes, fault-tolerant quantum computation, and quantum machine learning. The
course will also cover physical implementations of quantum computation into
real quantum computers and their programming languages using real-world
examples utilizing a state-of-the-art quantum technology through the IBM Q
Experience, Microsoft
Quantum Development Kit, and D-Wave
Leap. Topics to be covered will likely include: o Introduction, bra-ket notation, unitary operations, orthogonal
measurements, n-qubit states, entanglement, single-qubit and controlled
operations o Super
dense coding, incomplete measurements, quantum teleportation o Quantum
Computing Computer Architectures o Quantum
Computing Languages o The
quantum circuit model of computation o Quantum error-correcting codes and fault-tolerance o Basic quantum algorithms like Deutsch-Josza, Simon, and Grover o Shor's factoring algorithm o Computational complexity theory o Quantum entanglement, teleportation, and Bell
inequalities o Quantum Fourier transforms and the hidden subgroup
problem o Quantum query complexity, span programs, and the
adversary method o Density matrices, state discrimination, tomography o Von Neumann entropy and Holevo's
bound o Quantum machine learning Evaluation o The course
evaluation will consist of 4 assignments (10% each) on basic quantum theory
and algorithmic. Some assignments will also involve programming real quantum
computers using web enabled IBM Q and D-Wave access. o Most of the marks
will be on a final project (50%) that must include basic quantum computing
applications and its implementation on a real quantum computer or a
simulator. |
Lecture Notes
|
Lecture
Date |
Topics |
Slides
and Texts |
Assignments |
|
Jan. 11 |
Introduction |
|
|
|
Jan. 18 |
Origin of
Quantum Mechanics and History of Quantum Computing |
|
|
|
Jan. 25 |
Intro. To
Complex Linear Algebra and Hilbert Space Special
case for Classical Bits (CBit) and Quantum Bit (Qbit) |
More on Dirac Notation and Hilbert Space |
|
|
Feb. 1 |
Classical
Bit and Quantum Bit Manipulations Basic
Quantum Bit Operations |
|
Assignment 1: Solve the following mat
problems QC Math1 In
addition, please follow the tutorials and document the results. Due date
Feb. 8 |
|
Feb. 8 |
Circuit
model of quantum computation |
|
|
|
|
Time Reversal Using Quantum Computer??? |
|
|
|
Feb. 15 |
o The Deutsch-Jozsa algorithm o Simonís algorithm o Quantum Fourier transform and periodicities o Quantum algorithms for search problems o Shor quantum factoring algorithm o IBM
Programming Environment |
|
Assignment 2: Read the following and run the
Quantum circuits. Explain how it works and document the results.
Due date Feb. 22 |
|
Feb. 22 |
No class Reading Week |
|
Project Description Due Mar. 1 |
|
Mar. 1 |
o Universal Set Gates o Groverís quantum search algorithm o Microsoft Q# Language |
Quantum Computing at Microsoft |
Assignment 2 Extra: Homework2 Assignment 3: Read the following
and run the provided quantum circuits. Explain how it works and document the
results. Due
date Mar. 8 |
|
Mar. 8 |
o Adiabatic Quantum Algorithm o Adiabatic Quantum Hardware o D-Wave Programming Environment |
How The
Quantum Annealing Process Works.mp4 Measuring
Quantum Physics in a Quantum Annealer.mp4 Physics
of Quantum Annealing - Hamiltonian and Eigenspectrum.mp4 |
Assignment 4: The main
goal of this assignment is to learn how to use the D-Wave programming
environment o Factoring
with the D-Wave System Report
the results with an analysis Due
date Mar. 22 |
|
|
Time Reversal is it for Real? |
|
|
|
Mar. 15 |
o Quantum Computer Hardware o How to Design a Qbit o Fault-tolerant quantum error correction Fault-tolerant
quantum gates, Eastin-Knill theorem Microsoft QC Hardware |
Quantum Computer Hardware
Overview Quantum-Computer-Compiler.pptx |
|
|
Mar. 22 |
Quantum
Cryptography |
||
|
Mar. 29 |
Quantum
Machine Learning |
||
|
Apr. 5 |
Project
Presentations |
Shrimanti
Ghosh Quantum
Neural Networks with Continuous-Variable Formalism Thea Wang
Implementing
Quantum Computing on Solving Linear Systems of Equations Zhaorui
Chen A Quantum
Collaborative Filtering Framework Zhi Han Root Finding with
Quantum Computer Ayantha
Randika Implementing a Quantum Genetic
Algorithm Satchel
Jeanne Armena Integer
Factorization through Quantum Annealing Bradley
Swanson |
|
Background Reading
- A Rosetta Stone for Quantum Mechanics with an
Introduction to Quantum Computation by Samuel J. Lomonaco, JR.
- An Introduction to Quantum Computing for Non-Physicists by
Eleanor Rieffel and Wolfgang Polak
Books
- Quantum Computer Science by David Mermin (2007)
- Quantum Computing for Computer Scientists by
Yanofsky, Noson S. and
Mirco A. Mannucci
(2008)
- Quantum Computation and Quantum Information by
Nielsen and Chuang (2010)
- Classical and Quantum Computation by Kitaev, Shen, and Vyalyi
(1999)
- Quantum Information Theory by Mark
Wilde (2013)
- An Introduction to Quantum Computing by
Phillip Kaye, Raymond Laflamme, and Michele Mosca
(2007)
- Quantum Computing Explained by McMahon,
David (2008).
Other Lecture Notes
- Quantum Computation by David Mermin
- Quantum Computation by Umesh Vazirani
- Quantum Computation by John Preskill
- Theory of Quantum Information and Introduction to
Quantum Computing by John Watrous
- Quantum algorithms by Andrew Childs
- Quantum Computing Since Democritus by
Scott Aaronson
- Quantum Computing by David Bacon
- Quantum Computation and Information by
Ryan O'Donnell, John Wright
- Quantum Computing by Peter Shor
- Qubits, Quantum Mechanics, and Computers by
Birgitta Whaley, Kevin Young, Mohan Sarovar
- Topics in Quantum Computing by Don Towsley and Bo Jiang with videos
- Quantum Computing by Ronald de Wolf
with full-fledged lecture notes
- Great Ideas in Theoretical Computer Science by
Scott Aaronson with lectures on Quantum Computing and Quantum Algorithms
Quantum Computing Devices/Simulators
- DWave and its software incl. qbsolv
- Quantum Apprentice for Excel, see
- qOp v2.5 for Linux, see qOp_linux_INSTALL_0.pdf.
Actually, I prefer this setup:
tar xzf qOp.linux_2.5.0.1.tar
cd qOp/bin
cp dw_setup dw
chmod 755 dw
cd ..
export DWAVE_HOME=`pwd`/projects-cvs/dwave-x2/v2.5/qOp
export PATH=$PATH:$DWAVE_HOME/bin
export LD_LIBRARY_PATH=$DWAVE_HOME:$LD_LIBRARY_PATH
cp $DWAVE_HOME/.dwrc ~/ - qOp v2.5 for OSX, see qOp_osx_INSTALL_1.pdf
- qOp v2.5 for Windows, see
qOp_win32_INSTALL_0.pdf
- IBM's QX and qiskit plus talk (slides/video)
- Introduction to Quantum Computing
- Quantum Algorithm Implementations for Beginners (with
IBM examples)
- Quantum Neural Network (Japan)
- Microsoft's Q#
- ScaffCC Compiler
- QX Quantum Computer Simulator from QuTech / TU Delft (joint with Intel)
- List of Quantum Computing Tools
- qmasm and edif2qmasm
(EDIF Verilog to DWave Qmasm) from
Scott Pakin (LANL)
- Quirk web-based gate-model simulator
w/ Grover
algorithm
- recommended for Quirk users: Quantum computing for the determined Utube video series by Michael Nielsen
- QuTiP Quantum Toolbox in Python
(for Physics problems)
Papers/Talks
- From Cbits to Qbits: Teaching Computer Scientists Quantum Mechanics by
David Mermin
- Design of a Superconducting Quantum Computer by
John Martinis (UCSB+Google QUantum
AI)
- Adiabatic Quantum Computation by Vicky
Choi (VT)
- A Layered Software Architecture for Quantum Computing
Design Tools by Svore at al.,
IEEE Computer ( Volume: 39, Issue: 1, Jan. 2006 )
- ScaffCC: A Framework for Compilation and Analysis of Quantum
Computing Programs. Ali JavadiAbhari,
Shruti Patil, Daniel Kudrow, Jeff Heckey, Alexey
Lvov, Frederic T. Chong, Margaret Martonosi. ACM
International Conference on Computing Frontiers, May 2014. Best Paper
Award. ScaffCC on github. related slides
- Software and Architectures for Large-Scale Quantum
Computing, Fred Chong, U. Chicago
- Compiler Management of Communication and Parallelism
for Quantum Computation. Jeff Heckey,
Shruti Patil, Ali JavadiAbhari, Adam Holmes,
Daniel Kudrow, Ken Brown, Diana Franklin, Margaret Martonosi,
Frederic T. Chong. Architectural Support for Programming Languages and
Operating Systems (ASPLOS), March 2015.
- more papers by Fred Chong U Chicago
- A Software Methodology for Compiling Quantum Programs,
Thomas Häner, Damian S. Steiger,
Krysta Svore, Matthias Troyer, arXiv:1604.01401,
some slides
- D-Wave pubs suitable for presentation:
- A practical heuristic for finding graph minors by
Jun Cai, Bill Macready, Aidan Roy
- Discrete optimization using quantum annealing on
sparse Ising models, Bian et al., Front. Phys., 18 September 2014
- Other D-Wave pubs:
- Experimental Demonstration of a Robust and Scalable
Flux Qubit by Harris et al., arXiv:0909.4321v1
- Architectural considerations in the design of a
superconducting quantum annealing processor by Bunyk et al., arXiv:1401.5504
- Entanglement in a Quantum Annealing Processor by
Lanting et al., arXiv:1401.3500
- Gates for Adiabatic Quantum Computing by
Richard H. Warren, arXiv:1405.2354, 2014
- Ground State Spin Logic by J. D.
Whitfield, M. Faccin, J. D. Biamonte,
arXiv:1205.1742, 2012
o Performance Models for Split-execution Computing Systems by
Travis S. Humble, Alexander J. McCaskey, Jonathan Schrock, Hadayat
Seddiqi, Keith A. Britt, Neena
Imam, arXiv:1607.01084
o A quantum macro assembler by Scott Pakin, High Performance Extreme Computing Conference
(HPEC), 2016, QMASM github code
o QX: A high-performance quantum computer simulation platform by
Khammassi et al., DATE'17
o Quantum Error Correction for Beginners by
Simon J. Devitt, Kae Nemoto, William J. Munro,
arXiv:0905.2794
o Quantum Computing over Finite Fields: Reversible Relational
Programming with Exclusive Disjunctions by Roshan P. James,
Gerardo Ortiz, Amr Sabry, arXiv:1101.3764
o Quantum Supremacy through the Quantum Approximate
Optimization Algorithm, Edward Farhi, Aram
W Harrow, arXiv:1602.07674 (Submitted on 24 Feb 2016)
o Error mitigation for short-depth quantum circuits,
Kristan Temme, Sergey Bravyi, Jay M. Gambetta (Submitted on 6 Dec 2016 (v1),
arXiv:1612.02058, last revised 6 Nov 2017 (this version, v3))
o Physics: Hybrid Quantum-Classical Approach to Correlated Materials,
Bela Bauer, Dave Wecker, Andrew J. Millis, Matthew B.
Hastings, and Matthias Troyer, Phys. Rev. X 6, 031045, 21 September 2016
o Chemistry: A
variational eigenvalue solver on a photonic quantum processor, A. Peruzzo et al., Nature Comms 5, 4213 (2014)
o Quantum supremacy: Quantum
advantage with shallow circuits by Sergey Bravyi,
David Gosset, Robert Koenig in arXiv:1704.00690, Apr 2017, also in Science, 19 Oct 2018: Vol. 362, Issue 6412, pp.
308-311, DOI: 10.1126/science.aar3106, slides, video