5. Radix Sort

For the present we will look at one further sorting algorithm. This one is different, it is not based on the general algorithm strategy above, but on a totally different method. It is interesting because it requires the absolute minimum amount of space and the minimum amount of data movement, and, most amazing of all, it does no comparisons.

The sorting algorithm is called Radix Sort. It is ideal if you are using linked lists with integer keys. It sorts elements by looking at their KEY values one digit at a time. First it sorts them according to their least significant digit. It sorts the result of this according to the second least significant digit. And carries on like this until, at last, it has sorted according to the most significant digit.

Radix Sort Revealed

To illustrate this let's start with the list of 3-digit integers.

: Write this list vertically on the board, with lots of space to the right.

362 745 885 957 054 786 080 543 012 565

Because the keys consist of base 10 digits we will need an array of 10 buckets (linked lists) indexed by the possible values of the digits.

: Draw this to the right of the list:

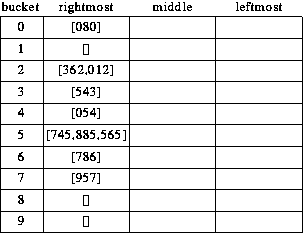
In the First Pass through the list, we look only at the least significant (rightmost) digit.

362 goes in bucket #2.
745 goes in bucket #5.
885 goes in bucket #5 - it is added after 745. In general, the contents of each bucket is a list; new values are added at the end of the list. This is not essential in the first pass, but it is absolutely essential in all the others. Bucket #5 now contains the list [745,885].
957 goes in bucket #7.
054 goes in bucket #4.
786 goes in bucket #6.
080 goes in bucket #0 (because of its rightmost 0, not the leftmost one).
543 goes in bucket #3.
012 goes in bucket #2. 362 is already there, 012 gets added after it. Bucket #2 now contains [362,012].
565 goes in bucket #5. The result is the list [745,885,565].

That's the end of the first pass. It doesn't look like much has really been accomplished, but wait and see! Here is the state of the buckets now.

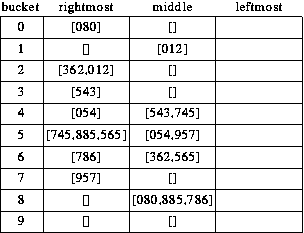
In the second pass we go through the buckets created in the first pass, doing them in order from 0 to 9, and, within each bucket, from first to last. In this pass we look only at the middle digit.

080 goes in bucket #8.
362 goes in bucket #6.
012 goes in bucket #1.
543 goes in bucket #4.
054 goes in bucket #5.
745 goes in bucket #4. The result is [543,745].
885 goes in bucket #8. The result is [080,885].
565 goes in bucket #6. The result is [362,565].
786 goes in bucket #8. The result is [080,885,786].
957 goes in bucket #5. The result is [054,957].

That's the end of the second pass. It still doesn't look like much has really been accomplished - be patient. Here is the state of the buckets now.

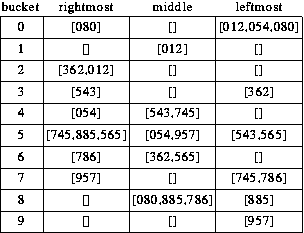
Now for the third pass. This is the final one, because each number has three digits. If there were more digits we'd just continue in the same manner digit by digit from right to left. Believe it or not, when we finish this pass the numbers will be sorted.

In this pass we look only at the high order (leftmost) digit.

012 goes in bucket #0. We know for sure it is the smallest value in the list, because we are on the last pass and it is the first value in the first bucket.
543 goes in bucket #5.
745 goes in bucket #7.
054 goes in bucket #0. We now know it's the second smallest number.
957 goes in bucket #9.
362 goes in bucket #3.
565 goes in bucket #5. The result is [543,565]. On previous passes we sometimes got sorted lists within buckets by chance. On the last pass this is guaranteed to happen.
080 goes in bucket #0. It is the third smallest value.
885 goes in bucket #8.
786 goes in bucket #7.

We are now completely finished sorting. All we have to do is join up all the lists in all the buckets in order to create the final sorted list.

It should be clear that the amount of work (adding things to the end of the lists in the buckets, and removing things from the front of these lists) is proportional to:

(Length of the original list) * (number of digits)