

Insertion
Because our heaps are complete trees, we know where the new node must
go. We have no choice, it must go in the bottom level, as far left as
possible. The new value is placed in this node. We then check if the
resulting tree is a heap: the place chosen for the new node guarantees
that the structural property will be satisfied, but the ordering
property might be be violated. The ordering property is re-established
by the `SIFT UP' operation.
The `SIFT UP' operation starts with a value in a leaf node. It
moves the value up the path towards the root by successively
exchanging the value with the value in the node above. The operation
continues until the value reaches a position where it is less than its
parent, or, failing that, until it reaches the root node.
Example:
insert 29 into the above heap.
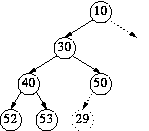
`29' must start where indicated; then it is sifted up.
Complexity = O(height) = O(logN)




