Deleting a Value From a Heap

1. V must not be in the resulting heap
2. the resulting heap must be a complete tree.

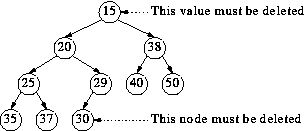
Condition (2) tells us which node must disappear: we must take away the rightmost node in the bottom level. This node must be `deleted' even if it is not the node containing V!

Example: delete 15 (the root) from this tree:

So we end up with a value (30) that has no node, and a node (`15') that has no value. The algorithm, then, is obvious.

1. save the value, X, in the rightmost node in the bottom level then delete this node.

2. Put X into the node containing V and then SIFT X UP, if it is smaller than its parent, or SIFT it DOWN if it is larger than either of its children.

Example: Delete 15 - delete the bottom right node, put its value (30) in the node where 15 was. 30 is smaller than 20 so we sift 30 down, with the final result:

Example: Delete 50 from this tree - delete the bottom right node, put its value (37) in the node where 50 was. 37 is smaller than 38 so we sift 37 UP, with the final result:

A special case of the DELETE operation is GET_SMALLEST, which returns the smallest value in a given heap and deletes the value from the heap.

How do you find the smallest value in a heap?

Answer: It is always in the root.