

In general, the relation between Height (H) and the number of nodes (N) in a tree can vary from H = N (degenerate tree) to H = log(N).
For efficiency's sake, we would like to guarantee that H was O(logN). One way to do this is to force our trees to be height-balanced.
A tree is perfectly height-balanced if the left and right subtrees of any node are the same height. e.g.
It is clear that at every level there are twice as many nodes as at the previous level, so we do indeed get H = O(logN). However, perfect height balance is very rare: it is only possible if there are exactly 2^H-1 nodes!
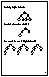
As a practical alternative, we use trees that are `almost' perfectly height balanced. We will say that a tree is height-balanced if the heights of the left and right subtree's of each node are within 1. The following tree fits this definition:
We will say this tree is height-balanced.
How can we tell if a tree is height-balanced? We have to check every node. The fastest is way is to start at the leaves and work your way up. When you reach a node, you will know the heights of its two subtrees; from that you can tell whether it is height-balanced and also compute the node's height (for use by its parent). For example, in the tree above
C and D are leaves. Their subtrees are all height 0 so C and D are both perfectly balanced. Having finished D we can compute the heights of B's subtrees.
B is not perfectly balanced, but the heights of of its subtrees differ only by 1, so B is regarded as height-balanced. Now we can compute the balance of A.
Like B, A's two subtrees differ by 1 in height. We have now looked at every node; every one is height-balanced, so the tree as a whole is considered to be height-balanced.
What about this tree - is it height-balanced?
Answer: no.
Finally, what about this one?
Answer: no (check node B).