AIxploratorium
Decision Trees - Page 6

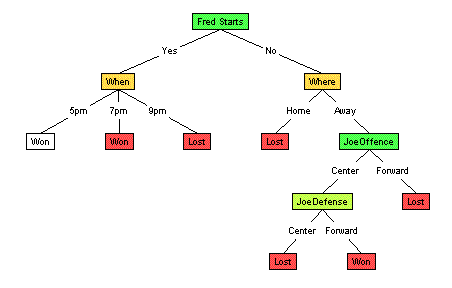
Evaluation Process + Cross Validation

You should have produced the tree shown below:

For comparison, the tree grown using InformationGain is:

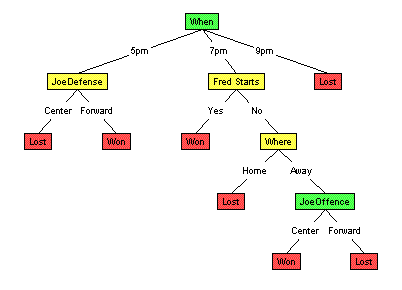
Evaluating Decision Trees

Hmmm... so now we have 2 different decision trees. Both are correct over the "training cases" --- the set of games whose outcomes we already know. And they have comparable size. Note, however, they give different answers here: The current tree, based on Gain Ratio, claims that the MallRat's will win.

Two different splitting criteria, leading to two different trees, leading to two different outcomes. Which outcome should we predict --- ie, which tree should we believe?

To help address this... recall that our goal is to predict the unknown outcome of a future game --- a challenge which is subtly different from correctly predicting the outcome of the known games. Here, it would be useful to see, for example, whether either tree could correctly predict the outcome of tomorrow's game, between the MallRats and the SnowBlowers. This is not our immediate task, which is to predict the outcome of next week's MallRat/Chinook game; we hope to use it, however, to help us determine which tree seems more correct.

Of course, we need to know the outcome of that MallRat/SnowBlower game, before we can use it in evaluating our two trees... which is not known, as that game has not been played.

However, we can use this basic idea -- of evaluating our learners based on the performance of their trees on unseen examples. The challenge, of course, is finding a source of "unseen examples": examples that the learner has not seen, but which we can see, and then use to evaluate the performance of the various classifiers obtained.

Why not use the examples we already have? For example, rather that train on all 20 games, we could instead train only on the first 19 games --- ie, not show the learner the final game:

(The complete dataset is here.)

The two learners (using Information Gain and Gain Ratio resp.) would each learn their respective trees based only on the first 19 games. We could then see which tree did best on the (unseen by the learner) 20^th game. Now if we find the InfoGain-based tree was correct on this 20^th game but the GainRatio-based tree was not, we would probably be more inclined to believe that Information Gain worked better than Gain Ratio, at least in this situation. ... and in the situation where we considered all 20 games. We would therefore use the InfoGain-based learner.  (Otherwise, if if GainRatio was correct but Gain was not, we would use the Gain Ratio-based tree.)

Cross-Validation

This is the basis for Cross-Validation: giving several learners only a subset of the training sample, then evaluating them on the remaining "hold-out" set. Here, are suggesting the idea of training on 19 records and testing on the 20^th.

To state this more precisely (sorry about the notation): Let IG₁₉ be the tree learned using the InformationGain splitting criterion, on the first 19 games and GR₁₉ be the tree learned using the GainRatio splitting criterion, on these 19 games; similarly IG₂₀ (resp, GR₂₀) is the tree learned using InformationGain (resp, GainRatio) on all 20 games. If IG₁₉ does well on the "unseen by the learner" 20^th game but GR₁₉ does not, then we would figure InformationGain seemed like a good idea, and so use IG₂₀ to classify the upcoming MallRat/Chinook game.

Of course, this only gives the outcome of a single game, and it is quite possible that both learners would be correct here (eg, both claim the MallRats will win) or both would be wrong. ... which would not help us discriminate between the two classifiers IG₁₉ and GR₁₉ and hence the two learners (based on Gain and Gain Ratio). It may be better instead to train on, say, the first 15 games, then compare the resulting decision trees on the remaining 5 games --- ie, determine the relative scores of IG₁₅ and GR₁₅, over these final 5 games. See chart.

This latter approach would give us a fairly accurate measure of the quality of the 2 decision trees produced (based on Gain and GainRatio). Wny not go even further, and train on 1 game, then test on the remaining 19? This would provide an even more accurate measure of the quality of the 2 decision trees produced, IG₁ based on Gain and GR₁ based on GainRatio. However, those two trees would (we expect) be worse than the trees produced using all 20 examples; that is we expect IG₁ to be less accurate than IG₁₅, which in turn is less accurate than IG₂₀; and similarly GR₁ is inferior to GR₁₅ will is inferior to GR₂₀.

Why less accurate? Our learning task has a lot in common with "estimating" some quantity --- eg, estimating the height of typical adult men. If we examine only one or two men, we are not likely to see a representative sample of men, and so the empirical average of the observed heights may not be correct. However, as we see more and more men, the empirical average is more and more likely to be close to the true average height. That is, we expect to get better estimates with more examples; in our current learning context, we similarly expect that IG₂₀ will be superior to IG₁₅. (See Relation to Estimation.)

Size of HoldOut Set

The only reason to use IG₁₅, rather than IG₂₀, is to help us contrast Gain versus Gain Ratio, as that means we have labeled instances "left over", which we use to evaluate the different learners. We still need some way to divide the given "labeled sample" into the "training sample" (shown to the various learning algorithms) and the "holdout sample" (used to evaluate the quality of the results produced by these algorithms). As suggested above, we need a large training sample to produce accurate decision trees, but we also need a large holdout sample to be able to identify which of these decision trees is really best. Of course, as these sets are disjoint, making one larger necessarily makes the other smaller...

For notation: we call the error on the training set the "resubstitution error"; this measures how well the learned decision tree can do, when tested on the data that it was trained on. By contrast, there is an underlying distribution of labeled instances (representing all possible games that the MallRats might play); the error, over this distribution, is called the "true error" or "generalization error". Note that we are interested in the generalization error, as this will allow us to predict the result of the future MallRat/Chinook game. It turns out that the error on the hold-out set is, in general, an unbiased estimate of the true error. By constrast, the resubstitution error is typically "overly optimistic" --- that is, this error score is typically LOWER than the true error, which means any decision based on this score is problematic. Eg, a classifier (such as a decision tree) might have 0% resubstitution error (as the decision tree fit the training data perfectly) but still have a very large true error.

What is a good partitioning? There are lots of ideas here -- given a training sample of m "labeled instances", perhaps use m * 0.632 instances for training and the remaining m * 0.368 for evaluation. (Why?)

There are many other ideas, including k-fold cross-validation and leave-one-out cross-validation.

Try it now

To create a holdout dataset (which the applet calls a "Testing" dataset), follow the steps below:

• Go back to the applet and clear the current tree by choosing "Initalize" from the "Algorithm" menu. Make sure you're still viewing the "Basketball" dataset.
• Hold down the <Ctrl> key and click on four or five examples (rows) at random from the "Basketball - Training Examples" table (in the upper left "Dataset View" panel). Each row you pick will be highlighted in yellow.
• Pull down the "Dataset" menu and choose the "Move to Testing Set" option to move the examples you selected into a new holdout dataset. You can use the "Show Testing/Training Set" option under the "Dataset" menu to toggle the table view between the training and testing/holdout datasets.

Now that you've created a holdout dataset, it's time to see how well a tree built using just the training data will perform on the holdout examples.

• First, make sure the splitting function is set to "Gain" or "Gain Ratio". This will keep our new tree at a reasonable size.
• Select "Run" from the "Algorithm" menu. You should see a new tree, created using the training examples.
• The pie chart, in the upper left-hand corner of the "Tree View" panel, should report that the tree correctly classifies 100% of the training examples (stated another way, the tree has zero "resubstitution" error, as we would expect).
• If you right-click on the "Tree View" panel, a popup menu will appear. Select the "Show Testing Results option to view the tree's performance on the holdout examples. Some nodes in the tree will change color, and the pie chart will now report the number of holdout examples that have been correctly classified.

If you were lucky, the tree might have correctly classified all the holdout examples. It's likely, however, that there were one or two (or more) holdout examples that the tree didn't properly classify. One way to reduce the number of errors is by "pruning" the tree, which is the subject of a later section...