Lecture 8 - Our Specification Of Binary Tree

3.2. Our Specification Of Binary Tree - Details

Let us now look at the details of the specification of the abstract type Binary Tree.

Structure

a binary tree is either empty, or it consists of a component value, and optional left and right subtrees (binary).

Note: a subtree exists only if it is not empty.

I use the phrases ``empty subtree'' and ``no subtree'' interchangeably, they mean exactly the same thing. I normally do not draw empty subtrees when I draw a tree (likewise ``subtree is empty'' means exactly the same thing as ``subtree does not exist'').

Direction (related type)

A direction will be used to describe the relationship between two trees or subtrees - Left and Right refer to the subtrees of a tree, Up refers to a subtree's parent.

Core Operations

Notational Conventions: T, T1, T2 are binary trees, V a component value, D a direction.

The basic creation operations are the usual ones - CREATE_EMPTY and DESTROY - plus one new one: CREATE_SINGLETON which, as discussed above, obviates the need for an INSERT operation.

IS_EMPTY is self-evident.

GET_ROOTVALUE does just what its name says; it is the counterpart of the GET_VALUE operation we had for lists.

The counterpart of the list operations MOVE_FORWARD and MOVE_BACKWARD is:

GET_TREE

Input: T1 and D.
Output: T2.
Preconditions: if D = up, T1 must be a subtree. If D = left or right, the corresponding subtree must exist (i.e. be non-empty).
Postconditions: T2 is T1's left subtree, right subtree, or parent tree, as specified by D.

This is the way we move around in a tree ... we move `down' (or `forward') by getting successive subtrees and we move `up' by getting parent trees. For example, suppose T1 was:

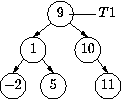
T2 = get_tree(T1,Left) would result in:

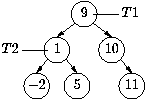
T2 is a subtree of T1. If we now did T2 = get_tree(T2,Left) we'd get:

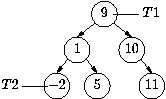
T2 = get_tree(T2,Up) would return us to the previous picture.

Note: The precondition that subtrees must exist... this means that GET_TREE never ever returns an empty tree. To check this precondition we use EXISTS.

EXISTS

Inputs: T and D.
Outputs: true or false.
Postconditions: true if there exists a tree in direction D.
- true if D is `up' and D is a subtree.
- true if D is `left' or `right' and T's subtree in direction D exists (i.e. is not empty).
- false otherwise

In other words:

D = left or right tests if T has a subtree in direction D.
D = up tests is D is a subtree, i.e. part of a larger tree (as opposed to being a whole tree).

This function should always returns false if T is empty. Why?

Answer: Because (1) empty trees have no subtrees, and (2) an empty tree can never be a subtree because empty subtrees do not exist - recall the preconditions for GET_TREE.

Example of these operations working together (traversal)

        void in_order_traverse(binary_tree *t, void (*f) (element))
        {
          if (! is_empty(t)) {
            if (exists(t,Left)) in_order_traverse(get_tree(t,Left),f);
            f(get_rootvalue(t));
            if (exists(t,Right)) in_order_traverse(get_tree(t,Right),f);
          }
        }

WHICH_SIDE

Input: T.
Output: a direction (`left' or `right').
Preconditions: T is a subtree
Postconditions: returns `left' if T is a left subtree, `right' if it is a right subtree.

Although this may seem a peculiar function, it is surprisingly useful. It is absolutely essential for doing non-recursive tree traversal, and many other applications.

JOIN

Inputs: T1, T2, and D.
Outputs: T1' and T2'.
Preconditions: D is not `up', T2 is not a subtree, T2 is not empty, and T1's subtree in direction D does not exist.
Postconditions: if T1 is empty, T1' is unified with T2. If T1 is nonempty, T1' has T2' as its subtree in direction D.

For example:

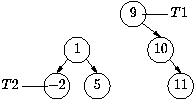
JOIN(T1,T2,Left) satisfies all the preconditions and produces:

The two preconditions that require explanation are:

T2 is not a subtree: we require this in order to avoid creating two trees that have a subtree in common.
T2 is not empty: empty subtrees do not exist.

PRUNE

Input: T.
Output: T'. The tree containing T is also changed.
Preconditions: T is a subtree (and therefore not empty).
Postconditions: T is unchanged, except it is no longer a subtree, and there is no longer any subtree in its place.

This is the exact inverse of JOIN. If we continue with the above example, and now do PRUNE(T2) the result is what we started with:

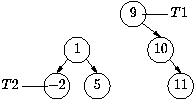
Note that the tree that T is a subtree of is not a parameter. We do not have a DELETE operation: we can achieve the same effect as DELETE(T) by the combination: PRUNE(T) and DESTROY(T).