1. Our Specification Of Lists - General Considerations

There is no unique way to specify an abstract data type. Last lecture we saw two `standard' specifications for lists, we will now develop our own. Specifications differ in two main ways:

what are the primitive parts out of which lists are composed.
what are the primitive operations on lists.

The choice of primitive operations is important, because it directly determines:

Functionality:

Users must write their functions using only the primitives that are provided. Some functions may be impossible to write with a given set of primitives. We must be sure that all the functions that might be needed by the user can be written using the primitives we provide.

For example, the primitive operations on arrays provided by Pascal do not permit the user to change the size of an array dynamically. This was a design decision made when Pascal was specified.

Efficiency:

How efficient will the user's code be?

User Convenience:

How much effort it will be for the user to write the functions he really needs? This is important because, in practice, the cost to develop software, and the number of tricky bugs that are in it, are closely linked with the amount of effort required to write the software.

For example, in the classical List specification, there is just one `current' node in any given list. This is actually very inconvenient: in many applications, it is necessary to access two elements of the same list simultaneously. It is not impossible to accomplish this within the classical specification, but doing so involves extra work and tricks which obscure the function being performed.

Maintainability:

A program is easily maintainable if it can easily be understood and changed. To ensure that the code that implements an abstract data type is very easily maintained, there should be as small a set of primitive operations as possible, and each primitive operation should be very simple.

We will view a list as a collection of elements that are organized in a linear fashion. The primitive operations that we will provide is determined by the following general considerations:

A list is a special kind of collection. In the most general notion of `collection' the elements in a collection are not organized in any particular way. Lists are collections having an additional property: the order on elements. There are many very powerful operations that can be defined on collections generally - we'll see several shortly - and we would like to be able to apply these to lists too.
We would like all our primitive operations to be very efficient. More precisely, we want them to be constant time and constant space operations - which means they will use the same time and space to process lists of any size. There will be obvious exceptions - operations which, by definition, must access each element in the list one-by-one - but all other operations should require constant time and space.
There are some very commonly-used operations that we would like to ensure are done as efficiently as possible. For example, one of the most common operations on a list or collection is determining its size (length). Another pair of common operations are joining together two lists and the inverse: splitting one list into two (the front and back). In the classical specification, these operations require going through the list element by element - therefore, they are not constant time operations - they are quick for short lists but very slow for very long lists. We will make them primitive operations and make them constant time.
We will generalize the classical idea of a current node: we will allow the user to access any number of list elements simultaneously. To do this, we will define an abstract type called window, which gives access to an element in a list; the user can have as many windows as he likes. We will have to define operations on windows, that permit them to be created, moved around, inspected, and so on.
We will not have any operations that result in the same element being a member of two different lists. This may sound strange, but it is a situation that can very easily arise, even with ordinary primitives like TAIL or our JOIN operation. To see this, consider the following example.

Suppose we have three lists,

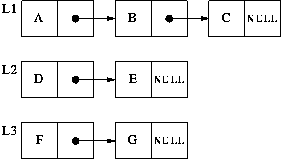
and we join L1 and L2 together using the JOIN operation. This operation captures the intuitive meaning of `join', resulting in list:

What is the relation between this list and the ones we started with? One possibility, which seems very natural, is that L1 and L2 have literally been glued together, so that L1 is the result of the operation (L2 has been glued onto the end of it), and L2 is the last 2 elements of L1:

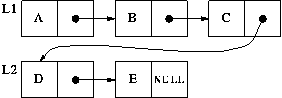
Why is this a problem? Well, because some operations on L2 will affect L1, and, likewise, some operations on L1 will affect L2. For example, if we now JOIN L1 and L3, L2 will be affected:

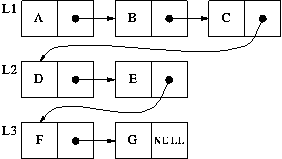
As you can imagine, if this happens, things get very confusing!

There are at least four ways to avoid this confusion:

return a copy. L1 and L2 are unaffected by JOIN. This solution tends to be memory hungry.
keep L1 and L2 completely separate: put all the elements that would normally be shared into just one of them. In this approach, JOIN(L1,L2) transfers the elements from L2 into L1: L2 ends up with nothing in it.
change the `type' of L2: it is now a `sublist' instead of a `list'. Then restrict some operations to operate only on lists, not on sublists (typically sublists can be inspected but not changed). This gives the advantages of sharing (efficient memory use) without the problems.
L1 and L2 become exactly the same list - all subsequent operations on one of them have identical effects on both. They become two names for the very same list: we say that they become `unified'.
```
        
```

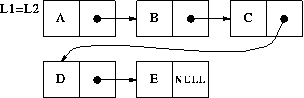
(2), (3), and (4) are equally acceptable. We will use (2) for lists, and (3) for trees later in the course. We will discuss (4) in more detail next lecture.

This decision is not a mere implementation detail. It is a crucial consideration in formulating our specification. It affects how we define the behaviour of our operations - we have just described 5 different ways the JOIN operation might behave. In order to write an application that uses JOIN, the applications programmer must know which of these five behaviours he will get.