# jemdoc: addcss{rbh.css}, addcss{jacob.css}
= nim game
~~~
{}{raw}
nim
tips
alg?
dag
equiv
memo
trace
time
demo
checkers
form
cgt
sol
~~~
~~~
{}{raw}
nim game
~~~
~~~
{your move: who wins ?}{}
*
*
*
*
* *
* * *
a b c
~~~
~~~
{nim game}
- k piles of stones
- on a move, player selects pile, removes any number stones from there
- last player to move wins
- [https://en.wikipedia.org/wiki/Nim nim wiki]
~~~
~~~
{}{raw}
algorithm tips
~~~
~~~
- use recursion
- avoid code duplication (e.g. negamax)
- avoid recomputation (e.g. memoization)
~~~
~~~
{memoization example}{}
def fib(n):
if n<=1: return n
return fib(n-2)+fib(n-1)
for j in range(40):
print(j, fib(j))
how long does this take to execute?
memoize, don't recompute
def dpfib(n):
F = [0,1]
for j in range(2,n+1):
F.append(F[j-1] + F[j-2])
return F[n]
~~~
~~~
{}{raw}
alg to solve nim (10 10 10 10 10) ?
~~~
~~~
- so far, tic-tac-toe, with simple minimax,alphabeta,negamax
- does this work for nim ?
- consider game state search tree for nim (10 10 10 10 10)
- move from root state (10 10 10 10 10)?
-- 1-10 from 1st pile or 2nd pile or ... or 5th pile
- so root state has 50 children, {{50*49}} grandchildren, ...
- at depth 10, this tree already has {{50*49*48*47* ... *41}} > 3 e16 nodes
- this tree too big ... what can we do ?
- answer: exploit isomorphisms and memoize
- as with tic-tac-toe, use a transposition table,
generate only one node per equivalence class (set of isomorphic states)
- eg. nim (1 2 3)
-- x remove 1 from pile a, y remove 1 from pile b
-- x remove 1 from pile b, y remove 1 from pile a
-- tree: these 2 paths lead to different nodes, but same state
- eg. tictactoe
-- x a1, o a2, x a3
-- x a3, o a2, x a1
-- again, tree: these 2 paths lead to different nodes, but same state
~~~
~~~
{solve nim(1 3 3) by hand}{}
0 0 0
0 0 1
0 0 2
0 0 3
0 1 1
0 1 2
0 1 3
0 2 2
0 2 3
0 3 3
1 1 1
1 1 2
1 1 3
1 2 2
1 2 3
1 3 3
start
0 0 0 L
0 0 1 ?
0 0 2 ?
0 0 3 ?
0 1 1 ?
...
next: states that get to losing state win
0 0 0 L
0 0 1 W
0 0 2 W
0 0 3 W
0 1 1 ?
...
next: states that get only to winning states lose
0 0 0 L
0 0 1 W
0 0 2 W
0 0 3 W
0 1 1 L <-
...
next: states that get to losing state win
0 0 0 L
0 0 1 W
0 0 2 W
0 0 3 W
0 1 1 L
0 1 2 W <-
0 1 3 W <-
0 2 2
0 2 3
...
next: states that get only to winning states lose
0 0 0 L
0 0 1 W
0 0 2 W
0 0 3 W
0 1 1 L
0 1 2 W
0 1 3 W
0 2 2 L <-
0 2 3
...
finished:
0 0 0 L 000
0 0 1 W 001
0 0 2 W 002
0 0 3 W 003
0 1 1 L 011
0 1 2 W 012
0 1 3 W 013
0 2 2 L 022
0 2 3 W 023
0 3 3 L 033
1 1 1 W 111
1 1 2 W 112
1 1 3 W 113
1 2 2 W 122
1 2 3 L 123
1 3 3 W 133
~~~
~~~
{}{raw}
game space search: dag vs tree
~~~
~~~
- dag: directed acyclic graph
- instead of search tree, use search dag
- ie. different paths from root can lead to same child
-- above tictactoe example: the 2 paths lead to same node
-- above nim example: the 2 paths lead to same node
- pro: fewer nodes in dag than tree, so less time to examine all nodes
- con: dag code usually more complicated than tree code, especially
if information from child is backed up to parent
-- tree: each child has 1 parent
-- dag: each child can have many parents
~~~
~~~
{}{raw}
state equivalence
~~~
~~~
- compress search space by grouping nodes into equivalence classes
- eg. nim: put isomorphic states in same class
-- eg. (1 2 3) {{≡}}
(1 3 2) {{≡}}
(2 1 3) {{≡}}
(2 3 1) {{≡}}
(3 1 2) {{≡}} (3 2 1)
~~~
~~~
{eg. nim (1 2 3)}{}
number states ?
(1+1)*(2+1)*(3+1) = 24
number non-isomorphic states ?
12
123
012 013 023 112 113 122
001 002 011 022
000
~~~
~~~
{nim (2 2 2) dag}
{{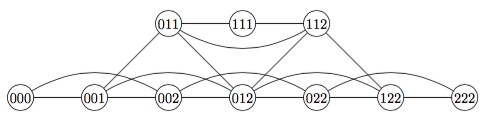 }}
- root node (222)
- all arcs go from right to left, eg. 222 has children 122, 022
- exercise: put an x under each losing state, put an arrow on each winning edge
~~~
~~~
{}{raw}
}}
- root node (222)
- all arcs go from right to left, eg. 222 has children 122, 022
- exercise: put an x under each losing state, put an arrow on each winning edge
~~~
~~~
{}{raw}
memoization
~~~
~~~
- also called dynamic programming
-- instead of recomputing, write and lookup
- memoization approach:
works if states can be ordered so that
value of a state depends only on values of previous states
~~~
~~~
{dp nim algorithm}
- order states by number of stones
-- so each move results in state with fewer stones
- in order, fewest stones to most,
-- compute win/loss value for each state
~~~
~~~
{algorithm to compute nim values}
definition
- position is *losing* if
every move from that position is to a winning position
- vacuously: any position with no moves is losing
- position is *winning* if is not losing, ie. if
some move from that position is to a losing position
algorithm
- value{{[ 0 0 ... 0 ] <- Loss}} ~ ~ (state with no stones is losing)
- (consider states by increasing number of total stones)
- for j in range{{[1 .. max possible number of stones]}}:
-- for each state k with j stones:
-- if value{{[ k ]}} not yet defined:
--- for each state w that can move to k: {{value[ w ] <- win}}
correctness? ~ ~ because we consider states
by increasing number of stones,
if the value of a state is not yet defined by the time we
get to it, it must be the case that every move from that
state is to a state whose value we have already seen,
and (since we would have set the value otherwise) all those
values must be wins, so the value of the undefined state
must be a loss
~~~
~~~
{dynamic program nim solver}{}
for each state:
value(state) = False
for k in range(1, sum_pilesizes):
for each k-stone state:
if not value(state):
for each state t reachable by adding stones to a pile of s:
value(t) = True
~~~
~~~
{}{raw}
trace dpsolve (3 3 3)
~~~
~~~
{}{}
showing sorted equiv classes only
0 stones: 000 F, update 001 002 003 T
1 stones: 001 T, no update
2 stones: 002 T
011 F 012 013 111 112 113 T
3 stones: 003 T
012 T
111 T
[exercise: show trace output for 4 stones]
...
~~~
~~~
{}{raw}
time
~~~
~~~
{dp nim solver runtime}
- each state causes an update at most one time
- number of states at most product_pilesizes
- each update takes time at most sum_pilesizes
- total time O(product_pilesizes * sum_pilesizes)
~~~
~~~
{}{raw}
demo dp nim solver
~~~
~~~
{}{}
- simple/nim/nim.py
~~~
~~~
{}{raw}
solving checkers
~~~
~~~
{solving games/puzzles: when dp works well ?}
- when number of positions (or equivalence classes) eventually
drops to a manageable number
- eg. [https://webdocs.cs.ualberta.ca/~mmueller/ps/ijcai05checkers.pdf solving checkers]
- 1994 (1996): Schaeffer's checkers program Chinook first *bot* to be world champion of some game
- 2007: Schaeffer's program solves checkers (a draw)
- key idea to solving checkers: endgame databases (dp on steroids)
- see picture of checkers search space in above paper
- quote from above paper:
/Using retrograde analysis, subsets
of a game with a small number of pieces on the board can
be exhaustively enumerated to compute which positions are
wins, losses or draws. Whenever a search reaches a database
position, instead of using an inexact heuristic evaluation function,
the exact value of the position can be retrieved./
~~~
~~~
{}{raw}
~~~
~~~
*theorem* a nim position losing if and only if
xorsum of pile sizes is 0
eg: {{xorsum(1 2 3) = 01 ^ 10 ^ 11 = 00}}, so (1 2 3) is losing.
eg: {{xorsum(3 5 3) = 011 ^ 101 ^ 111 = 001}}, so (3 5 7) is winning.
how to find a winning move? from (3 5 7) can move to
(0 5 7) xorsum 010 winning, no
(1 5 7) xorsum 011 winning, no
(2 5 7) xorsum 000 losing, yes
exercise: find all other winning moves from (3 5 7)
~~~
~~~
{sketch of proof}
*show* for each state P with xorsum 0, each move
is to state with xorsum nonzero
- each move is from pile j with p_j > 0
- let c_j be column of leftmost 1 in binrep p_j
- remove any number of stones from p_j
changes xorsum of column c_j from 0 to 1
- so xorsum(new P) has c_j 1, so nonzero
*show* for each state P with xorsum nonzero,
some move is to state with xorsum 0
- let c_j be column of leftmost 1 in binrep xorsum(P)
- let p_x be any pile with 1 in c_j
- z = xorsum(P ^ p_x) has 0 in all columns c_1 ... c_j,
so z < p_x, so can reduce p_x to z, leaves state with xorsum zero
~~~
~~~
{all winning moves}{}
def nimreport(P): # all nim winmoves from P, use formula
total = xorsum(P) # xor all elements of P
if total==0:
print(' loss')
return
for j in P:
tj = total ^ j # xor
if j >= tj:
print(' win: take',j - tj,'from pile with',j)
[ code: simple/nim/bignim.py ]
~~~
~~~
{nim formula example}{}
all winmoves from (1 2 6)
1 0 0 1
2 0 1 0
6 1 1 0
xor+ 1 0 1 <-- nonzero, so exists winmove
1-pile winmove?
after move, need new total xorsum 0, so
need to remove k = (xorsum of all other piles) stones
(xorsum of all other piles) = 110 ^ 010 = 100 = 4
remove 4 stones from 1-pile? 4 > 1 *no*
2-pile winmove?
remove 001 ^ 110 = 7 stones? 7 > 2 *no*
6-pile winmove?
remove 001 ^ 010 = 3 stones? 6 > 3, *yes*
after remove 3 from 6-pile:
1 0 0 1
2 0 1 0
3 0 1 1
sum 0 0 0 <--- losing state, as desired
- exercise: find all winmoves from (3 5 6 7)
~~~
~~~
{}{raw}
combinatorial game theory
~~~
~~~
- nim is one of the games whose math gave rise to combinatorial game theory
- combinatorial game:
-- includes games where *whoever cannot move loses*
-- variant: whoever cannot move wins
- math of cgt is essential to solving go endgame puzzles
- some cgt games
-- amazons
-- breakthrough
-- clobber
-- dots and boxes
~~~
~~~
{}{raw}
exercise solutions
~~~
~~~
{nim (1 2 6): who wins?}{}
*
*
* only win:
* take 3 from
* * pile c, leave
* * * (1 2 3)
a b c
~~~
~~~
{nim dp trace}{}
4 stones: 013 T
022 F 023 122 222 223 T
112 T
...
~~~
~~~
{nim (3 5 6 7): all winning moves}{}
3 0 1 1
5 1 0 1
6 1 1 0
7 1 1 1
sum 1 1 1
* piles 5,6,7 have 1 in this column
winning: remove 3 from 5-pile, leaves
3 0 1 1
2 0 1 0
6 1 1 0
7 1 1 1
sum 0 0 0 or
remove 5 from 6-pile, leaves
3 0 1 1
5 1 0 1
1 0 0 1
7 1 1 1
sum 0 0 0 or
remove all from 7-pile, leaves
3 0 1 1
5 1 0 1
6 1 1 0
0 0 0 0
sum 0 0 0
~~~
~~~
{nim (2 2 2) dag}
{{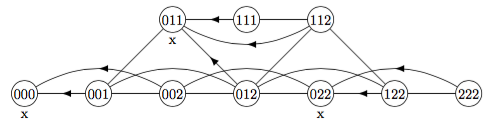 }}
~~~
}}
~~~
 }}
- root node (222)
- all arcs go from right to left, eg. 222 has children 122, 022
- exercise: put an x under each losing state, put an arrow on each winning edge
~~~
~~~
{}{raw}
}}
- root node (222)
- all arcs go from right to left, eg. 222 has children 122, 022
- exercise: put an x under each losing state, put an arrow on each winning edge
~~~
~~~
{}{raw}
 }}
~~~
}}
~~~