nim game
nim game
*
*
*
*
* *
* * *
a b c
k piles of stones
on a move, player selects pile, removes any number stones from there
last player to move wins
algorithm tips
use recursion
avoid code duplication (e.g. negamax)
avoid recomputation (e.g. memoization)
def fib(n):
if n<=1: return n
return fib(n-2)+fib(n-1)
for j in range(40):
print(j, fib(j))
how long does this take to execute?
memoize, don't recompute
def dpfib(n):
F = [0,1]
for j in range(2,n+1):
F.append(F[j-1] + F[j-2])
return F[n]
alg to solve nim (10 10 10 10 10) ?
so far, tic-tac-toe, with simple minimax,alphabeta,negamax
does this work for nim ?
consider game state search tree for nim (10 10 10 10 10)
move from root state (10 10 10 10 10)?
1-10 from 1st pile or 2nd pile or … or 5th pile
so root state has 50 children, 50*49 grandchildren, …
at depth 10, this tree already has 50*49*48*47* ... *41 > 3 e16 nodes
this tree too big … what can we do ?
answer: exploit isomorphisms and memoize
as with tic-tac-toe, use a transposition table, generate only one node per equivalence class (set of isomorphic states)
eg. nim (1 2 3)
x remove 1 from pile a, y remove 1 from pile b
x remove 1 from pile b, y remove 1 from pile a
tree: these 2 paths lead to different nodes, but same state
eg. tictactoe
x a1, o a2, x a3
x a3, o a2, x a1
again, tree: these 2 paths lead to different nodes, but same state
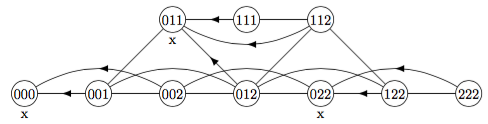
0 0 0 0 0 1 0 0 2 0 0 3 0 1 1 0 1 2 0 1 3 0 2 2 0 2 3 0 3 3 1 1 1 1 1 2 1 1 3 1 2 2 1 2 3 1 3 3 start 0 0 0 L 0 0 1 ? 0 0 2 ? 0 0 3 ? 0 1 1 ? ... next: states that get to losing state win 0 0 0 L 0 0 1 W 0 0 2 W 0 0 3 W 0 1 1 ? ... next: states that get only to winning states lose 0 0 0 L 0 0 1 W 0 0 2 W 0 0 3 W 0 1 1 L <- ... next: states that get to losing state win 0 0 0 L 0 0 1 W 0 0 2 W 0 0 3 W 0 1 1 L 0 1 2 W <- 0 1 3 W <- 0 2 2 0 2 3 ... next: states that get only to winning states lose 0 0 0 L 0 0 1 W 0 0 2 W 0 0 3 W 0 1 1 L 0 1 2 W 0 1 3 W 0 2 2 L <- 0 2 3 ... finished: 0 0 0 L 000 0 0 1 W 001 0 0 2 W 002 0 0 3 W 003 0 1 1 L 011 0 1 2 W 012 0 1 3 W 013 0 2 2 L 022 0 2 3 W 023 0 3 3 L 033 1 1 1 W 111 1 1 2 W 112 1 1 3 W 113 1 2 2 W 122 1 2 3 L 123 1 3 3 W 133
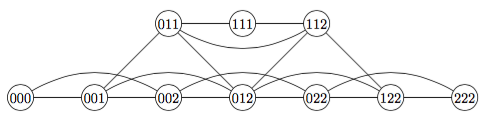
game space search: dag vs tree
dag: directed acyclic graph
instead of search tree, use search dag
ie. different paths from root can lead to same child
above tictactoe example: the 2 paths lead to same node
above nim example: the 2 paths lead to same node
pro: fewer nodes in dag than tree, so less time to examine all nodes
con: dag code usually more complicated than tree code, especially if information from child is backed up to parent
tree: each child has 1 parent
dag: each child can have many parents
state equivalence
compress search space by grouping nodes into equivalence classes
eg. nim: put isomorphic states in same class
eg. (1 2 3) ≡ (1 3 2) ≡ (2 1 3) ≡ (2 3 1) ≡ (3 1 2) ≡ (3 2 1)
number states ?
(1+1)*(2+1)*(3+1) = 24
number non-isomorphic states ?
12
123
012 013 023 112 113 122
001 002 011 022
000
root node (222)
all arcs go from right to left, eg. 222 has children 122, 022
exercise: put an x under each losing state, put an arrow on each winning edge
memoization
also called dynamic programming
instead of recomputing, write and lookup
memoization approach: works if states can be ordered so that value of a state depends only on values of previous states
order states by number of stones
so each move results in state with fewer stones
in order, fewest stones to most,
compute win/loss value for each state
definition
position is losing if every move from that position is to a winning position
vacuously: any position with no moves is losing
position is winning if is not losing, ie. if some move from that position is to a losing position
algorithm
value[ 0 0 ... 0 ] <- Loss (state with no stones is losing)
(consider states by increasing number of total stones)
for j in range[1 .. max possible number of stones]:
for each state k with j stones:
if value[ k ] not yet defined:
for each state w that can move to k: value[ w ] <- win
correctness? because we consider states by increasing number of stones, if the value of a state is not yet defined by the time we get to it, it must be the case that every move from that state is to a state whose value we have already seen, and (since we would have set the value otherwise) all those values must be wins, so the value of the undefined state must be a loss
for each state:
value(state) = False
for k in range(1, sum_pilesizes):
for each k-stone state:
if not value(state):
for each state t reachable by adding stones to a pile of s:
value(t) = True
trace dpsolve (3 3 3)
showing sorted equiv classes only
0 stones: 000 F, update 001 002 003 T
1 stones: 001 T, no update
2 stones: 002 T
011 F 012 013 111 112 113 T
3 stones: 003 T
012 T
111 T
[exercise: show trace output for 4 stones]
...
time
each state causes an update at most one time
number of states at most product_pilesizes
each update takes time at most sum_pilesizes
total time O(product_pilesizes * sum_pilesizes)
demo dp nim solver
- simple/nim/nim.py
solving checkers
when number of positions (or equivalence classes) eventually drops to a manageable number
eg. solving checkers
1994 (1996): Schaeffer's checkers program Chinook first bot to be world champion of some game
2007: Schaeffer's program solves checkers (a draw)
key idea to solving checkers: endgame databases (dp on steroids)
see picture of checkers search space in above paper
quote from above paper:
Using retrograde analysis, subsets of a game with a small number of pieces on the board can be exhaustively enumerated to compute which positions are wins, losses or draws. Whenever a search reaches a database position, instead of using an inexact heuristic evaluation function, the exact value of the position can be retrieved.
nim formula
theorem a nim position losing if and only if xorsum of pile sizes is 0
eg: xorsum(1 2 3) = 01 ^ 10 ^ 11 = 00, so (1 2 3) is losing.
eg: xorsum(3 5 3) = 011 ^ 101 ^ 111 = 001, so (3 5 7) is winning.
how to find a winning move? from (3 5 7) can move to
(0 5 7) xorsum 010 winning, no
(1 5 7) xorsum 011 winning, no
(2 5 7) xorsum 000 losing, yes
exercise: find all other winning moves from (3 5 7)
show for each state P with xorsum 0, each move is to state with xorsum nonzero
each move is from pile j with p_j > 0
let c_j be column of leftmost 1 in binrep p_j
remove any number of stones from p_j changes xorsum of column c_j from 0 to 1
so xorsum(new P) has c_j 1, so nonzero
show for each state P with xorsum nonzero, some move is to state with xorsum 0
let c_j be column of leftmost 1 in binrep xorsum(P)
let p_x be any pile with 1 in c_j
z = xorsum(P ^ p_x) has 0 in all columns c_1 … c_j, so z < p_x, so can reduce p_x to z, leaves state with xorsum zero
def nimreport(P): # all nim winmoves from P, use formula
total = xorsum(P) # xor all elements of P
if total==0:
print(' loss')
return
for j in P:
tj = total ^ j # xor
if j >= tj:
print(' win: take',j - tj,'from pile with',j)
[ code: simple/nim/bignim.py ]
all winmoves from (1 2 6) 1 0 0 1 2 0 1 0 6 1 1 0 xor+ 1 0 1 <-- nonzero, so exists winmove 1-pile winmove? after move, need new total xorsum 0, so need to remove k = (xorsum of all other piles) stones (xorsum of all other piles) = 110 ^ 010 = 100 = 4 remove 4 stones from 1-pile? 4 > 1 *no* 2-pile winmove? remove 001 ^ 110 = 7 stones? 7 > 2 *no* 6-pile winmove? remove 001 ^ 010 = 3 stones? 6 > 3, *yes* after remove 3 from 6-pile: 1 0 0 1 2 0 1 0 3 0 1 1 sum 0 0 0 <--- losing state, as desired - exercise: find all winmoves from (3 5 6 7)
combinatorial game theory
nim is one of the games whose math gave rise to combinatorial game theory
combinatorial game:
includes games where whoever cannot move loses
variant: whoever cannot move wins
math of cgt is essential to solving go endgame puzzles
some cgt games
amazons
breakthrough
clobber
dots and boxes
exercise solutions
*
*
* only win:
* take 3 from
* * pile c, leave
* * * (1 2 3)
a b c
4 stones: 013 T
022 F 023 122 222 223 T
112 T
...
3 0 1 1
5 1 0 1
6 1 1 0
7 1 1 1
sum 1 1 1
* piles 5,6,7 have 1 in this column
winning: remove 3 from 5-pile, leaves
3 0 1 1
2 0 1 0
6 1 1 0
7 1 1 1
sum 0 0 0 or
remove 5 from 6-pile, leaves
3 0 1 1
5 1 0 1
1 0 0 1
7 1 1 1
sum 0 0 0 or
remove all from 7-pile, leaves
3 0 1 1
5 1 0 1
6 1 1 0
0 0 0 0
sum 0 0 0