np hard problems
exact (accept non-poly time)
brute force
backtracking
branch and bound
heuristic (accept non-optimal)
approximation (non-optimal, but some bound?)
brute force
n variables: 2n possible assignments
backtracking
consider partial solutions, abort when partial cannot extend
branch and bound (optimization problems)
keep upper bound on extension value
abort extension when bound less than best value of some complete solution
#generate random t-uniform formula
import random
# literals x1 -x1 x2 -x2 ... output as 1 -1 2 -2 ...
# for sorting clauses,
# literals 1 -1 2 -2 ... n -n represented by
# integers 0 1 2 3 ... n-2 n-1
def litToInt(lit):
if lit>0: return 2*lit-2
return 2*(-lit)-1
def intToLit(n):
if 0==n%2: return 1+n/2
return -(1+n/2)
def randclause(n,k): # n-var uniform random k-clause
# floyd's alg, from Bentley's prog. pearls "A sample of brilliance"
# if lit in clause then -lit not in clause
S = []
for j in range(n+1-k,n+1):
t = random.randint(1,j)
if S.count(t)>0: S.append(j)
else: S.append(t)
S.sort()
for j in range(k):
if random.randint(0,1)==0: S[j] *= -1
return S
def formula(n,t,m): # n variables, t-uniform, m clauses
f = []
while len(f)<m:
new = randclause(n,t)
duplicate = False
for j in f:
if new == j: duplicate = True
if not duplicate: f.append(new)
# sort lexicographic using x1 < -x1 < x2 < -x2 < ...
for m in range(len(f)):
for c in range(len(f[m])): f[m][c] = litToInt(f[m][c])
f.sort()
for m in range(len(f)):
for c in range(len(f[m])): f[m][c] = intToLit(f[m][c])
return f
def prettyClause(c):
psn = -1
for lit in c:
psn, psnOld = litToInt(lit), psn
for j in range(psn-(psnOld+1)): print ' ',
print '%2d' % lit,
print ''
def plainClause(c):
print '[',
for j in range(len(c)-1): print '%2d,' % c[j],
print '%2d]' % c[len(c)-1]
def show(f,pretty):
for c in f:
if pretty: prettyClause(c)
else: plainClause(c)
f = formula(5,3,20)
show(f,False)
show(f,True)
# literals x_1 ... x_n represented by 1 2 ... n
# literals -x_1 ... -x_n represented by -1 -2 ... -n
def clausesat(clause,asnmt):
for var in clause:
if ((var>0 and asnmt[var-1]==1) or
(var<0 and asnmt[-(var+1)]==0)):
return True
return False
def sat(formula, asnmt):
for clause in formula:
if not clausesat(clause,asnmt): return False
return True
def showf(f):
for j in f: print j
n,m = 10,40 #max m is n choose k times 2^k, where k=2or3
allAsn = itertools.product([0,1],repeat=n)
myf = randsat.formula(3,n,m)
print "\nrandom formula",n,"vars",m,"clauses"
showf(myf)
for a in allAsn:
if sat(myf,a):
print a
break
S <- original problem
while not S.isempty()
P <- S.pop()
P yields solution?
yes: return "solved"
no:
maybe: add resulting subproblems to S
return "no solution"
subproblems ?
set next variable TRUE
set next variable FALSE
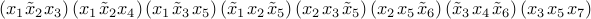
subproblems:
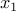 F/T,
F/T, 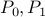
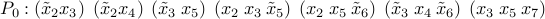
subproblems:
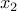 F/T,
F/T, 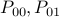
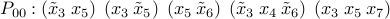
no solution (2-clauses), abort this subproblem
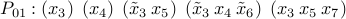
must have
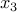 T,
T, 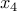 T,
T, 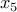 T, solution
T, solution
return solution: F T T T T * *
better: Davis-Putnam-Logemann–Loveland
# assignment vector: one entry for each variable
# set a[0] to UNSAT if formula unsatisfiable
UNSAT, UNKNOWN, FALSE, TRUE = -2, -1, 0, 1
def emptyAsnmt(n):
a = [UNKNOWN]*n
return a
def showf(f):
for j in f: print j
def showfa(f,a):
for x in a: print x,
print ''
showf(f)
def fixliteral(t, f, a): # in f, set literal t True, update a
index = abs(t)-1
#print "set var",index+1, ("T" if t>0 else "F")
assert a[index]== UNKNOWN
a[index] = (TRUE if t>0 else FALSE)
for clause in f[:]:
clauseSat = False
for literal in clause[:]:
if literal == -t:
clause.remove(literal)
if len(clause)==0: # f unsat
a[0] == UNSAT
return
elif literal == t:
clauseSat = True
if clauseSat: f.remove(clause)
def mycopy(f,a):
newa = list(a)
newf = []
for clause in f: newf.append(list(clause))
return newf, newa
def sat(f): return (True if len(f)==0 else False)
def unsat(a): return (True if a[0]==UNSAT else False)
def backsat(f,a):
if unsat(a): return f,a
if sat(f): return f,a
minj = f.index(min(f,key=len)) # clause with fewest literals
if len(f[minj])==0:
a[0]= UNSAT
return f,a
if len(f[minj])==1:
fixliteral(f[minj][0], f, a)
return backsat(f,a)
#split: 2 possible bool. vals for literal f[minj][0]
#print "split A:", f[minj][0]
fcopy, acopy = mycopy(f,a)
fixliteral(f[minj][0], f, a)
f,a = backsat(f,a)
if sat(f): return f, a
f,a = fcopy, acopy
#print "split B:", -f[minj][0]
fixliteral(-f[minj][0], f, a)
return backsat(f, a)
n,m = 6,20 #max m is n choose k times 2^k, where k=2or3
myf = randsat.formula(3,n,m)
asn = emptyAsnmt(n)
showfa(myf, asn)
f,a = backsat(myf,asn)
showfa(f,a)
for typical subpath, e.g. AXCDR…
a lower bound on an extension is:
cost of subpath AXCDR, plus …
min cost edge from A to rest of vertices, plus …
min cost edge from R to rest of vertices, plus …
MST cost on rest of vertices
A 1 B
4 | | 3
H - - - - - 2 - - - - - C
2 5 4 5
G - - - - - 6 - - - - - D
6 | | 1
F 3 E
start anywhere, say A
AB: bound ? cost AB, 1 +
min edge A to rest of vertices, 4 +
min edge B to rest of vertices, 3 +
MST on rest of vertices, 13 = 21
AF: bound ? cost AF, 5 +
min edge A to rest, 1 +
min edge F to rest, 3 +
MST on rest, 13 = 22
AH: bound ? cost AH, 4 +
min edge A to rest, 1 +
min edge H to rest, 2 +
MST on rest, 17 = 24
so try AB first ...
ABC: bound 22
ABE: bound 25 so try ABC first ...
ABCD: bound 25
ABCH: bound 23 so try ABCH first ...
ABCH extends uniquely to to ABCHGDEFA, cost 23
... ABCD (>= 25) cannot be better
... ABE (>= 25) cannot be better
... AH (>= 24) cannot be better
At this point, we can stop: have found best
tour that starts from A and next vertex is one of B,H
(and every such TSP has this property; if we explore AF...
we will just find our TSP in reverse).
greedy algorithm (repeatedly pick set covering most uncovered vertices) gives log-base-2(n) approx ratio
not hard to find inputs that achieve this ratio
classic 1.5 approximation for metric (i.e. satisfying triangle inequality) TSP