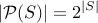sets

counting, subsets, binom. coef., pascal tri.,

why counting ?

fibonacci numbers

  • compare iterative and recursive programs

  • which is faster ?

  • iterative version: about 2n arithmetic operations

  • recursive version ?

    • total number of function calls: r(n) = 1 + r(n-1) + r(n-2)

    • r(0) = 1     r(1) = 1

    • notice: for n ≥ 0,   r(n) = 2f(n+1) - 1

    • exercise: prove by induction

    • f(100) = 354224848179261915075

    • r(100) = 1146295688027634168201

section 1: see text

  • set notation

  • set properties and proofs

    • algebraic rules for sets

    • Venn diagrams and proofs of set equations

    • element method for proofs of set equations

    • tabular method for proofs of set equations

    • an algebraic proof

  • ordering sets

    • lex order

      • really, defined only for sequences

      • for (multi-)sets, first order elements in (multi-)set

subsets etc

intro

binomial coefficients

theorem

  • defn: for integers n,k, C(n,k) = number of k-element subsets of n-set

  • defn: for non-negative integer n, n!

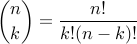
  • defn: for non-negative integers n,k, {displaystyle{n choose k} = frac{n!}{k!(n-k)!}}

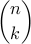
  • theorem: C(n,k) = {displaystyle{n choose k}}

  • proof: in text

why values C(n,k) called binomial coefficients ?

because of this identity:

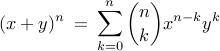
(x + y)^n : = : sum_{k=0}^{n} {nchoose k} x^{n-k}y^{k}
combinatorial identity

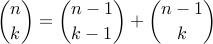
for integers 0 ≤ k ≤ n,     displaystyle {nchoose k} = {n-1choose k-1}+{n-1choose k}

  • proof: consider n-set with 1 element marked

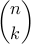
    • k-subsets ?     displaystyle {nchoose k}

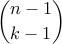
    • k-subsets with marked element?     displaystyle {n-1choose k-1}

    • k-subsets without marked element?     displaystyle {n-1choose k}

    • QED

pascal's triangle

pascal(11)
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]
[1, 6, 15, 20, 15, 6, 1]
[1, 7, 21, 35, 35, 21, 7, 1]
[1, 8, 28, 56, 70, 56, 28, 8, 1]
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]
[1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]
[1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1]
computing Pascal's triangle
#   assume n at least 1
#   print rows 0..n of Pascal's triangle
def pascal(n):
    print [1] # row 0
    a = [1,1]
    print a   # row 1
    for j in range(n-1): # j = 0..n-2
        a.append(1)
        a.reverse()
        for k in range(j+1):
            a[k+1] += a[k+2]
        print a  #row j+2
representing subsets

  • consider set U = { a, b, …, k }

  • to describe subset S of U:

    • can list elements, eg. S = { c, f, g, k }

    • can give characteristic vector, eg. S = (0 0 1 0 0 1 1 0 0 0 1)

    • (0 0 0 0 0 0 0 0 0 0 0) represents what subset ?

    • (1 1 1 0 0 0 0 0 0 0 0) represents what subset ?

another combinatorial identity

for non-negative integers n,

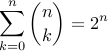
sum_{k=0}^{n} {nchoose k} = 2^n

proof

  • sum is total number of subsets of n-set

  • 1-1 correspondence between subsets of n-set and 0/1-n-vector

  • number 01-n-vectors = number n-sequences of 2-set = 2n

another proof

  • binomial coefficients identity, with x=y=1

power set

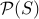
  • set of all subsets of set S is power set mathcal{P}(S)

  • by preceding identity,

| mathcal{P}(S) | = 2^{|S|}