logic
propositional logic
| boolean algebra | logic |
| 0/ 1 | T/F |
| bool. fn. | statement form |
| value | truth value |
| equality | equivalence |
- tautology
statement form, always T
(↔ boolean function, always 1)
- contradiction
statement form, always F
(↔ boolean function, always 0)
logical operators
| ~ | negation | complement | ||
| ∧ | and | conjunction | min | |
| ∨ | or | disjunction | max | |
| ⇔ | if and only if | equivalence | ⊕ | = |
| ⇒ | implies | ~( ) ∨ ( ) | ≤ | |
| ⇐ | implied by | ( ) ∨ ~( ) | ≥ |
| p | q | ∧ | ∨ | ⇔ | ⇒ | ⇐ |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
operator precedence
| ( ) | ~ | ∧ | ∨ | ⇒ | ⇔ |
implication
“if X then Y” corresponds to “X ⇒ Y”
but when X does not hold
English meaning of “if X then Y” may be ambiguous
logical value of “X ⇒ Y” is T (statement form is vacuously true)
p: "it is raining" q: "my hair is wet" value of p ⇒ q when . . .
it is raining and my hair is wet ?
it is raining and my hair is not wet ?
it is not raining and my hair is not wet ?
it is not raining and my hair is wet ?
contrapositive of p ⇒ q: ~q ⇒ ~p
equivalent
converse of p ⇒ q: q ⇒ p
inverse of p ⇒ q: ~p ⇒ ~q
equivalent to converse
let be p,q as above, let I be p ⇒ q . in English, state
I
contrapositive of I
converse of I
inverse of I
equivalent
if p then q
q only if p
p is sufficient for q
q is necessary for p
not p, or q
equivalent
p if and only if q
p is necessary and sufficient for q
equivalent
unless
or
equivalent
and
but
logic and sets
| boolean algebra | logic | sets |
| min | ∧ | ∩ |
| max | ∨ | ∪ |
| (1-x) | ~ | complement |
| min(p, max(q,r)) = | p ∧ (q ∨ r) ⇔ | P ∩ (Q ∪ R) = |
| max(min(p,q), min(p,r)) | (p ∧ q) ∨ (p ∧ r) | (P ∩ Q) ∪ (P ∩ R) |
predicate logic
- predicate
says something about its subject
- predicate logic
allows reasoning about statement collections
| ∀ | for all | universal quantifier | ∀ x ∈ D, S(x) |
| ∃ | exists, for some | existential quantifier | ∃ x ∈ D, S(x) |
 integers integers | 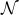 ≥ 0 ≥ 0 | 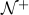 ≥ 1 ≥ 1 | 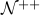 ≥ 2 ≥ 2 | 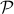 prime prime | 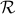 reals reals | 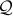 rationals rationals
|
∀ n ∈ 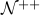 , ∃ p,q ∈
, ∃ p,q ∈ 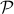 , p+q = 2n
, p+q = 2n
∀ n . . . ∃ p . . . means:
for each value of n, there is a particular p
for different values of n, the values of p may differ
∃ p . . . ∀ n . . . means:
there is some p, such that for this p and all values of n, . . .
∃ p,q ∈ 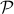 , ∀ n ∈
, ∀ n ∈ 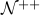 , p+q = 2n
, p+q = 2n
disprove this conjecture
negating quantifiers
| ~ ( ∀ x ∈ D, S(x) ) | ⇔ | ∃ x ∈ D, ~ S(x) |
| ~ ( ∃ x ∈ D, S(x) ) | ⇔ | ∀ x ∈ D, ~ S(x) |
all items not available in all stores ?
A(i,s)
- item i available at store s
∀ i ∈ I, ∀ s ∈ S, A(i,s)
- every item available in every store
∀ i ∈ I, ∀ s ∈ S, ~ A(i,s) ?
∀ i ∈ I, ~ ( ∀ s ∈ S, A(i,s) ) ?
~ ( ∀ i ∈ I, ∀ s ∈ S, A(i,s) ) ?
| ∀ i ∈ I, ∀ s ∈ S, ~ A(i,s) | ||
| ∀ i ∈ I, ~ ( ∀ s ∈ S, A(i,s) ) | ∀ i ∈ I, ∃ s ∈ S, ~ A(i,s) | |
| ~ ( ∀ i ∈ I, ∀ s ∈ S, A(i,s) ) | ∃ i ∈ I, ~ ( ∀ s ∈ S, A(i,s) ) | ∃ i ∈ I, ∃ s ∈ S, ~ A(i,s) |
every item in every store is unavailable ?
every item is unavailable in some store?
some item in some store is unavailable ?
it is not the case that every item is available in every store
not every item is available in every store
set min/max
- set
collection (possibly empty) of distinct elements
- finite set S
empty, or exists pos. int. t, elements can be labelled s1 . . . st
S = { } or ∃ t ∈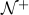 , S = { s1 . . . st }
, S = { s1 . . . st }- max
of S ⊆
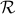 : x ∈ S, ∀ s ∈ S, x ≥ s
: x ∈ S, ∀ s ∈ S, x ≥ s- min
of S ⊆
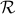 : y ∈ S, ∀ s ∈ S, y ≤ s
: y ∈ S, ∀ s ∈ S, y ≤ s
min/max of
{ 1, 3, 5 } ?
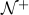 ?
? { r ∈
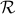 , 0 < r < 1 } ?
, 0 < r < 1 } ?
meaning?
∃ m ∈ S, ∀ s ∈ S, m ≥ s
∀ m ∈ S, ∃ s ∈ S, m < s
∃ n ∈
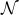 , ∀ s ∈ S, s < n
, ∀ s ∈ S, s < n∀ n ∈
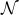 , ∃ s ∈ S, s ≥ n
, ∃ s ∈ S, s ≥ n
for every nonempty finite S ⊆ 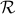 , S has max/min
, S has max/min
min ← max ← s_1
for j ← 2 to t
#invariant: max >= s_1, ..., s_{j-1}
if s_j < min then min ← s_j
if s_j > max then max ← s_j
prove by induction on t that, when program terminates, max is the value of the maximum element of S. hint: prove the invariant. remark: last time through the loop, j is set to t+1 in for-check
for every nonempty S ⊆ 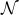 , S has min
, S has min
min ← any s in S for j ← min downto 0 # invariant: ? if is_in(j,S) and j < min then min ← j
find and prove invariants
for every nonempty S ⊆ 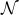 , S has max ⇔ S finite
, S has max ⇔ S finite
X: “S has max” F: “S is finite” want to show X ⇔ F.
first show X ⇒ F
assume X.
so S has max x.
so S ⊆ { 0, 1, . . . , x } .
so F.
next show F ⇒ X.
assume F.
use above theorem.
examples with quantifiers
S(p)
≡ (p ∈ 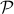 ) ∧ (p + 2 ∈
) ∧ (p + 2 ∈ 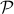 )
)
conjecture
∀ m ∈ 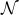 , ∃ p ∈
, ∃ p ∈ 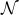 , (p > m) ∧ S(p)
, (p > m) ∧ S(p)
abc ≡ a(bc) Fn ≡ 1 + 22n wikipedia Q(n) ≡ Fn ∈ 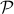
- Fermat conjecture
∀ n ∈
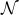 , Q(n)
, Q(n)
- Euler counterexample
not Q(5)
- open
∀ m ∈
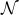 , ∃ n > m, Q(n) ?
, ∃ n > m, Q(n) ?
R(n) ≡ regular n-polygon straightedge/compass constructible wikipedia
- ancient Greeks
∀ k ∈
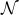 , R(3 ⋅ 2k) ∧ R(5 ⋅ 2k)
, R(3 ⋅ 2k) ∧ R(5 ⋅ 2k)
- Gauss
∀ m,k ∈
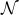 , m odd ⇒ ( R(m ⋅ 2k) ⇔ ∃ finite S ⊂
, m odd ⇒ ( R(m ⋅ 2k) ⇔ ∃ finite S ⊂ 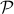 , ( ∀ s ∈ S, Q(s) ) ∧ (m = Π s ∈ S) )
, ( ∀ s ∈ S, Q(s) ) ∧ (m = Π s ∈ S) )
Mersenne number: Mn ≡ 2n - 1
Mersenne prime: Mersenne number and prime wiki
- open
∀ k ∈
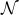 , ∃ p ∈
, ∃ p ∈ 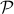 , ( (p > k) ∧ (Mp ∈
, ( (p > k) ∧ (Mp ∈ 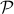 ) ) ?
) ) ?
- open
∀ k ∈
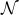 , ∃ t ∈
, ∃ t ∈ 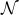 , ( (t > k) ∧ (Mt ∈
, ( (t > k) ∧ (Mt ∈ 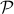 ) ) ?
) ) ?
- around 1637
Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos ejusdem nominis fas est dividere : cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.
∀ n ∈ 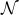 , n ≥ 3, ~ ( ∃ x,y,z ∈
, n ≥ 3, ~ ( ∃ x,y,z ∈  , xn + yn = zn )
, xn + yn = zn )
predicates: algebraic rules
- no quantifiers? same as prop. logic
P(x) ∨ ( Q(y) ∧ R(x,y) ) ⇔ ( P(x) ∨ Q(y) ) ∧ ( P(x) ∨ R(x,y) )
- quantifiers?
∀ x, ( P(x) ∧ Q(x) ) ⇔ ( ∀ x, P(x) ) ∧ ( ∀ x, Q(x) )
∀ x, ( P(x) ∨ Q(x) ) ?? ( ∀ x, P(x) ) ∨ ( ∀ x, Q(x) )
∃ x, ( P(x) ∧ Q(x) ) ?? ( ∃ x, P(x) ) ∧ ( ∀ x, Q(x) )
∃ x, ( P(x) ∨ Q(x) ) ⇔ ( ∃ x, P(x) ) ∨ ( ∃ x, Q(x) )