induction

history dominoes example problem:

∀ integers n ≥ 0	define s(n) = 0+1+…+n = 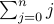$sum_{j=0}^{n} j$
∀ integers n ≥ 0	define f(n) = n(n+1)/2
∀ integers n ≥ 0	s(n) = f(n) ?

how proof by induction works
- prove claim holds in base case
- assume claim holds in arbitrary case (possibly base)
- prove claim holds in next case
domino analogy
- show that the 1st domino falls
- assume that an arbitrary domino falls
- show that, under this assumption, the next domino falls

claim ∀ integers n ≥ 0, s(n) = f(n)

base case: n = 0

s(0) = 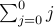$sum_{j=0}^{0} j$ = 0, and

f(0) = 0(0+1)/2 = 0, so claim holds in case case

inductive case

inductive hypothesis: let k be a fixed integer at least 0 (base case), and assume s(k) = f(k)
now we want to show s(k+1) = f(k+1), so

s(k+1)	=	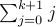$sum_{j=0}^{k+1} j$	defn s( )
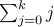	=	$sum_{j=0}^{k} j$ + k+1	regroup terms of s(k+1)
	=	s(k) + k+1	defn s( )
	=	f(k) + k+1	ind. hyp.
	=	k(k+1)/2 + k+1	defn f( )
	=	(k+1)(k+2)/2	arithmetic
	=	f(k+1)	defn f( )
			QED

induction song (copyright RBH 1998-2012)
to tune of Amazing Grace

chorus: induction is a very strange thing
        there are so many value for n
        oh how do we prove that something is true
        over and over again ?

the basis case we want to show
it's true for the smallest n
the inductive case we then will prove
it's true again and again.

        chorus

so assume it's true for n equals k
where k might be very small
then show it's true for k plus one
so then it's true for them all

        chorus