functions

defn, count, types, partitions, count by image, composition, perm.composititon, perm.cyc.form, perm.order,

function

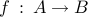
f : : : A rightarrow B

  • f (rule/map) from A (domain) to B (range)

representing functions on finite sets

  • dot/line diagram

    • dots for domain

    • dots for range

    • (dot x) — (dot y)    iff    f:x→y

  • as one-line notation sequence

    • eg. A = { a, b, c, d, e }     B = { 3, 7, 9 }

    • order elements of domain, eg. a b c d e

    • write vector ( f(a), f(b), f(c), f(d), f(e) ), eg. (7, 7, 3, 9, 7)

counting functions

number of functions f:A to B

  • = |B||A|

  • proof

    • number of |A|-sequences of an |B|-set

types of function f:A to B

surjection

  • for every b in B, exists ≥ one a in A, f(a) = b

  • onto

injection

  • for every b in B, exists ≤ one a, f(a) = b

  • one-to-one     (better: at-most-one - to - one)

bijection

  • for every b in B, exists exactly one a, f(a) = b

  • iff surjection and injection

  • matching

partitions

definition: partition of an n-set S

  • set P of subsets of S

  • each element of P, called a block, is non-empty

  • each element of S in exactly one element of P

  • e.g. S = { a b c d e }

    • P = { { a }   { c }   { b d e } }

    • Q = { { a }   { c }   { d e } } is not a partition of S

    • R = { { a }   { c }   { a d e } } is not a partition of S

S(n,k) = number of k-partitions of n-set

  • Stirling numbers of the 2nd kind

  • S(n,0) = 0   (why ?)

  • for n ≥ 1, S(n,1) = S(n,n) = 1   (why ?)

  • for n > k > 1:     pick element x of S

    • number k-partitions with block { x }   = S(n-1,k-1)

    • number k-partitions with block { x , … }   = kS(n-1,k)

  • for n > k > 1:     S(n,k) = S(n-1,k-1) + k S(n-1,k)

S(n,k)
n\k 0   1   2   3   4   5   6   7  ...
0   0                              ...
1   0   1                          ...
2   0   1   1                      ...
3   0   1   3   1                  ...
4   0   1   7   6   1              ...
5   0   1  15  25  10   1          ...
6   0   1  31  90  65  15   1      ...
7   0   1  63 301 350 140  21   1  ...

counting functions by image size

image, coimage

  • image of f:A to B       set { b ∈ B   |   ∃ a ∈ A, f(a) = b }

  • coimage of f:A to B       partition { f-1(b)   |   b ∈ image(f) }

number of functions from m-set to n-set with image size k

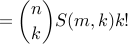
displaystyle = {nchoose k} S(m,k) k!

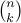
  • pick image: nchoose k

  • pick coimage: S(m,k)

  • match coimage blocks ↔ image elements: k!

number of surjections from m-set to n-set

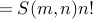
displaystyle = S(m,n) n!

  • why ?

  • surjection, so size of image = n

  • previous formula, k=n

  • eg. number of surjections from 6-set to 4-set is S(6,4)4!=1560

number of injections from m-set to n-set

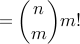
displaystyle = {n choose m} m!

  • why ?

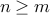  • injection, so size of image = m (and so n geq m)

  • previous formula, k=m

  • eg. number of injections from 4-set to 6-set is C(6,4)4!=360

function composition

defn

composition

composition of permutations

  • permutation p of A = { 1 … n } is function p:A to A

  • e.g. let p = (1 3 5 2 4)       (function in one-line form)

  • pp = (? ? ? ? ?)

    • pp(1) = p(p(1)) = p(1) = 1

    • pp(2) = p(p(2)) = p(3) = 5

    • pp(3) = p(p(3)) = p(5) = 4

    • pp(4) = p(p(4)) = p(2) = 3

    • pp(5) = p(p(5)) = p(4) = 2

  • so pp = (1 5 4 3 2)

  • p-1 = (? ? ? ? ?)

    • p(?) = 1     ?=1     so p-1(1) = 1

    • p(?) = 2     ?=4     so p-1(2) = 4

    • p(?) = 3     ?=2     so p-1(2) = 2

    • p(?) = 4     ?=5     so p-1(2) = 5

    • p(?) = 5     ?=3     so p-1(2) = 3

  • so p-1 = (1 4 2 5 3)

permutation: cyclic form

  • for permutation p:A to A, for every element a, sequence (a p(a) pp(a) ppp(a) … ) eventually cycles

  • e.g. p = (1 3 5 2 4)

    • (1)

    • (2 3 5 4)

    • (3 5 4 2)

    • (5 4 2 3)

    • (4 2 3 5)

  • so permutation is often described in cyclic form

cyclic form examples
one-line form              cyclic form
(1 2 3)                    (1) (2) (3)
(1 3 2)                    (1) (2 3)
(2 3 1)                    (1 2 3)
(1 3 5 2 4)                (1) (2 3 5 4)
(9 10 8 7 3 1 4 2 6 5)     (1 9 6) (2 10 5 3 8) (4 7)

permutation order

let p = (1) (2 3 5 4)     cyclic form

  • p0 = (1) (2) (3) (4) (5)       identity permutation

  • p1 = (1) (2 3 5 4)

  • p2 = (1) (2 5) (3 4)

  • p3 = (1) (2 4 5 3)

  • p4 = (1) (2) (3) (4) (5)

  • p5 = p4 p1 = p

  • p6 = p4 p2 = p2

  • p7 = p4 p3 = p3

  • p8 = p4 p4 = (1) (2) (3) (4) (5)

  • etc

order of permutation p = smallest positive integer t, pt = identity

permutation to a power
def addone(p):
  for j in range(len(p)): p[j]+=1
  return p

def permpower(p,t):
  q = []
  for j in range(len(p)): q.append(j)
  if t==0: return q
  for j in range(len(p)):
    indx = j
    for _ in range(t): indx = p[indx]-1
    q[j] = indx
  return q

#p = [9, 10, 8, 7, 3, 1, 4, 2, 6, 5]
p = [3,1,4,2]
print 'perm ',p
for t in range(5):
  print 'power',t,':', addone(permpower(p,t))
how to find order of permutation ?

e.g. p = (9 10 8 7 3 1 4 2 6 5)       one-line form

  • hint: find cyclic form of p

    • (9 10 8 7 3 1 4 2 6 5) (1 9 6) (2 10 5 3 8) (4 7)

powers of p
01   (1  9  6)  (2  0  5  3  8)    (4  7)
02   (1  6  9)  (2  5  8  0  3)    (4)(7)
03   (1)(6)(9)  (2  3  0  8  5)    (4  7)
04   (1  9  6)  (2  8  3  5  0)    (4)(7)
05   (1  6  9)  (2)(3)(5)(8)(0)    (4  7)
06   (1)(6)(9)  (2  0  5  3  8)    (4)(7)
..   .........  ...............    ......

??   (1)(6)(9)  (2)(3)(5)(8)(0)    (4)(7)