equivalence and order

eq.rel'n, bin.rel'n, which?, pigeonhole?, birthdays, php-div, posets, min coloring

equivalence relation

equivalence relation on a set S: defn
equivalent elements: in same block
equivalence class: block
example S={a,b,…,g}, partition={ {a,g} {c,d,f} {b} {e} }

example

let S = 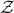define x ≡ y iff x = y (mod 4)
5 ≡ 9 ? (yes) 5 ≡ 99 ? (no)
equivalence classes:

example

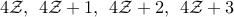
can use any function f:A→B to define an eq.rel.
define x ≡ y iff f(x) = f(y)
example f:{1,…,6}→{a,b,c,d} with f=(a,c,d,a,b,a)
here, partition is { {1,4,6} {2} {3} {5} }

binary relation

binary relation on a set S: a relation r:S→S (so, subset of S×S) defn
notation
- usually, R is the set of related order pairs
- xRy means (x,y) ∈ R
example S={a,..,f}, R={ (c,b) (d,a) (d,b) (e,e) }
- here, dRb ? (yes) bRd ? (no)

every equivalence relation is a binary relation

why ?

which binary relations are equivalence relations ?

RST

answer: every binary relation that is reflexive, symmetric, transitive

reflexive: for all x ∈ S, xRx
symmetric: for all x,y ∈ S, xRy iff yRx
transitive: for all x,y ∈ S, (xRy ∧ yRz) ⇒ xRz

exercise

for each relation: is it reflexive ? symmetric ? transitive ? an equivalence relation ? (if no, add the fewest ordered pairs that makes it an eq.rel.)

S = { a }, R = { }
S = { a }, R = { (a,a) }
S = { a,b }, R = { (a,b) (b,a) }
S = { a,b }, R = { (a,a) (a,b) (b,b) }
S = { a,b }, R = { (a,a) (a,b) (b,a) (b,b) }
S = { a,b,c }, R = { (a,a) (a,b) (b,a) (b,b) (c,c)}
S = { a,b,c }, R = { (a,b) (b,c) (a,c) }

how many …

binary relations on a k-set ? (why ?)
equivalence relations on a k-set ? (why ?)

example: fractions

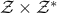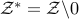
define S = $mathcal{Z}timesmathcal{Z}^{*}$ , where $mathcal{Z}^{*}=mathcal{Z}backslash 0$
define r:S→S by (a,b) R (c,d) iff a ⋅ d = b ⋅ c
(1,3) ≡ (2,4) ?
- no
(1,3) ≡ (3,9) ?
- yes
(0,1) ≡ (0,2) ?
- yes
(1,0) ≡ (2,0) ?
- no: neither (1,0) nor (2,0) are in S
exercise: verify that r is an equivalence relation
how does r represent equality of fractions ?

pigeonhole principle

theorem

every k-partition of an n-set has some block with at least 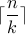$displaystyle lceil frac{n}{k} rceil$ elements

if there are n pigeons in a total of k holes, some hole has at least 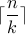$displaystyle lceil frac{n}{k} rceil$ pigeons

proof

let p_j = number pigeons in hole j. let m = max p_j.

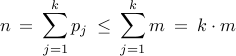
notice $displaystyle n : = : sum_{j=1}^{k} p_j : leq : sum_{j=1}^{k} m : = : kcdot m$

so displaystyle m geq n/k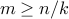

so some hole has ≥ n/k pigeons

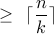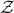so some hole has $displaystyle geq : : lceil frac{n}{k} rceil$ pigeons (since each p_j ∈ mathcal{Z} ) .

birthdays

birthday problem

how many people in a room so that, always, ≥ 2 have same birthday ?

k = 366 (number of different birthdays) n = number people
want smallest n so that n/k > 1
answer: n = 367

birthday paradox

how many people in a room so that, with probability ≥ .5, ≥ 2 have same birthday ?

answer: n = 23

PHP division problem

notice

let n = 3
does n divide any number, or difference of numbers, in {4,5} ?
does n divide any number, or difference of numbers, in {4,5,7}?
does n divide any number, or difference of numbers, in {a,b,c}, where a,b,c are fixed integers?

question

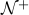
let n ∈ $mathcal{N}^+$
what is smallest integer k, so that for all S = { t₁, ... , t_k } ⊆ ,
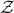- n divides some t_j or
- n divides some t_y - t_x ?

notice

neither property holds if k = n-1 and S = { 1, 2, …, n-1 }
so k ≥ n

notice

suppose k = n
first property holds if n divides some t_j
so assume n divides no t_j
so there are at most n-1 different values for t_j (mod n)
by PHP, exist t_x, t_y with same remainder (mod n)
so second property does not hold

conclusion

smallest integer above is k=n
for any set S, with k ≥ n, at least one of two properties holds

party trick

pick any sequence of five integers, eg. (9 -3 7 7 1)
find consecutive subsequence with sum a multiple of 5: (9 -3 7 7 *)
always possible ?

theorem

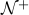for any n ∈ $mathcal{N}^+$ , any sequence (a₁ ... a_n), some consecutive subsequence has sum a multiple of n

proof

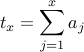
for each x ∈ {1, … n}, define $displaystyle t_x = sum_{j=1}^{x} a_j$
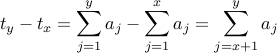
notice $displaystyle t_y - t_x = sum_{j=1}^{y} a_j - sum_{j=1}^{x} a_j = sum_{j=x+1}^{y} a_j$
by above conclusion, for S = { t₁, ..., t_j }, n divides some t_x or n divides some t_y - t_x
so, n divides some consecutive subsequence of (a₁ ... a_n)

partially ordered sets (posets)

what is a poset?

a binary relation that is
- reflexive
- antisymmetric
- transitive
e.g. S = subsets of {a,b,c} and relation "is subset of"
e.g. S = {1,2,…,12} and relation "divides"

what is a Hasse diagram?

a map of an IKEA store ? no
a simplified drawing of a poset:
- links that follow by transitivity are omitted

finding a min coloring of a poset

min coloring of a poset

stable set: a subset S of points of a poset, such that no two points of S are related
coloring (of points of poset): partition of points of a poset into stable sets (color classes)
min coloring: coloring with fewest number of color classes
finding a min coloring of a poset is easy (below)
finding min coloring of arbitrary binary relation can be harder

min coloring of poset
input: poset P
output: min coloring of P

j = 0
while not empty(P):
  C[j] = set of all sources of P
  remove C[j] from P
  j += 1

correctness

1) algorithm terminates
2) the partition is a coloring of P
3) the partition is a min coloring of P

the algorithm terminates

a binary relation with no cycles has a source
every poset has no cycles
so every iteration removes at least one point from P

the partition is a coloring

it suffices to prove that the set C of all sources of a poset is a stable set
suppose C is not stable
then it contains points a,b such that aRb
then b is not a source, and so should not be in C, contradiction

the coloring is minimum

it suffices to show that P has a chain of the same size as the number of color classes
to prove this, prove that every maximal chain contains a source
so the set C[0] intersects every maximal — and so also maximum — chain
finally, by induction, construct a chain of P that includes one point from every block (details omitted)