boolean functions: number, algebraic rules, rep'n thm, dnf/cnf

boolean functions

• 

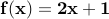
• function

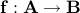
• rule/map, domain/input, range/output

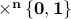• set of boolean n-tuples

• boolean function

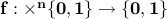
truth table

p	q	r	f(p,q,r)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

boolean operators

~	negation
∧	and	conjunction	min
∨	or	disjunction	max
⊕	xor	exclusive or	not equal

p	q	∧	∨	⊕
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

operator precedence

( )

~

∧

∨

p ∨ ~ r ∧ u     =     p ∨ ( (~r) ∧ u )

number n-variable bool. fn.

• consider n-variable truth table

• 2ⁿ rows

• each row, 2 choices for f( ) entry

• so num. diff't f( ) columns = 2⁽²ⁿ⁾

0,1,2-variables

0-variables

f( ) = 0, 1

1-variable

f(x) = 0, x, negations

2-variables

f(x,y) = 0, x, y, x∧y, x∨y, x⊕y, ~x∨y, x∨~y, negations

algebraic rules

~~p = p	double negation
p ◊ p = p	idempotent
p ◊ q = q ◊ p	commutative
p ◊ (p ∗ q) = p	absorption
p∧~p = 0 p∨~p = 1	negation
~(p ◊ q) = ~p ∗ ~q	DeMorgan
(p ◊ q) ◊ r = p ◊ (q ◊ r)	associative
p ◊ (q ∗ r) = (p ◊ q) ∗ (p ◊ r)	distributive
p∧0 = 0 p∧1 = p p∨0 = p p∨1 = 1	bound

◊ = ∧/∨         ∗ = ∨/∧ respectively

rep'n thm

proof (sketch)

case 0: 0 variables

case f( ) = 0: then f( ) = p∧~p = ~~(p∧~p) = ~(~p∨p)
case f( ) = 1: exercise

case 1: f( ) ≠ 0

so f( ) has a tabular representation, say
so f( ) = (x1 ∨ x2 ∨ … ∨ xk) where xj ↔ j'th input that gives output 1 notice that this is a disjunctive normal form (DNF) representation so to finish the proof …

eliminate

either ∨/∧ using ~~ and deMorgan

QED

example: represent f(p,q,r) defined above, using only ~ ∨ ∧

start ?

get DNF rep'n from truth table, so …

let

a = (~p ∧ ~q ∧  r)
b = (~p ∧  q ∧  r)
c = ( p ∧  q ∧ ~r)

f(p,q,r)

= a ∨ b ∨ c
= (~p ∧ ~q ∧ r) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ ~r)

example: represent f(p,q,r) defined above, using only ~ ∧

a,b,c as above

f(p,q,r)

= a ∨ b ∨ c
= ~~(a ∨ b ∨ c)
= ~( ~a ∧ ~b ∧ ~c)
= ~( ~(~p ∧ ~q ∧  r)   ∧ ~(~p ∧  q ∧  r)   ∧ ~( p ∧  q ∧ ~r)

example: represent f(p,q,r) defined above, using only ~ ∨

f(p,q,r)

= a ∨ b ∨ c
= ~~a ∨ ~~b ∨ ~~c
= ~~(~p ∧ ~q ∧  r)   ∨ ~~(~p ∧  q ∧  r)   ∨ ~~( p ∧  q ∧ ~r)
=  ~( p ∨  q ∨ ~r)   ∨ ~( p ∨ ~q ∨ ~r)   ∨ ~(~p ∨ ~q ∨  r)

dnf, cnf

disjunctive normal form

a1 ∨ a2 ∨ … ∨ at
where each aj is ∧ of ≥ 1 (negated) variable

conjunctive normal form

a1 ∧ a2 ∧ … ∧ at
where each aj is ∨ of ≥ 1 (negated) variable

rep'n thm

converts function into dnf

tabular to cnf

example: consider above f()

so ~f(p,q,r)

= v ∨ w ∨ x ∨ y ∨ z

where

v = (~p ∧ ~q ∧ ~r)
w = (~p ∧ q ∧ ~r)
x = (p ∧ ~q ∧ ~r)
y = (p ∧ ~q ∧ r)
z = (p ∧ q ∧ r), so

so f() = ~~f(p,q,r)

= ~(v ∨ w ∨ x ∨ y ∨ z)
= ~v ∧ ~w ∧ ~x ∧ ~y ∧ ~z
= (p ∨ q ∨ r) ∧ ~w ∧ ~x ∧ ~y ∧ ~z
= . . .