beans (variants and invariants)

beans, loops, example, inv.1, inv.2, var., post., another,

coffee beans

repeat
  bn1 := removeBean()
  bn2 := removeBean()
  if (bn1.col == white) ∧ (bn2.col == white) then
    putBlack()
  elsif (bn1.col == black) ∧ (bn2.col == black) then
    putBlack()
  else
    putWhite()

input/output ? preconditions ? postconditions ?

reasoning about loops

variant: nonneg. int. expression, decreases each iteration
invariant: expresssion, holds each time execution reaches it

a ≡ b (mod n)
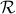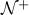a, b ∈ mathcal{R} n ∈ $mathcal{N}^+$ ∃ z ∈ mathcal{Z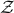} , a = b + n ⋅ z (so a,b differ by a multiple of n)

exercise

let w_k,b_k: number white,black beans after k iterations

let W,B: number white,black beans at start (so W=w₀, B=b₀)

use definition of mod

assume w_k = W (mod 2) and w_k+1 = w_k - 2

prove w_k+1 = W (mod 2)

simple example

# w/b: white/black beans in tin
# precondition: pos. int. W,B
w := W  b := B
while
  # invariant: w + b ≥ 1
  # invariant: w ≡ W (mod 2)
  # variant:   w + b
  w + b > 1
do
  bn1 := removeBean()
  bn2 := removeBean()
  if (bn1.col == white) ∧ (bn2.col == white) then
    putBlack()
  elsif (bn1.col == black) ∧ (bn2.col == black) then
    putBlack()
  else
    putWhite()
  endif
endwhile
# postcondition: w + b = 1
# postcondition: w ≡ W (mod 2)

1st invariant

proof of 1st invariant (by induction) (sketch)

w_t, b_t ≡ value of w,b after t iterations of loop body

1st time execution reaches inv. point: w₀ = W ≥ 1 b₀ = B ≥ 1 so
w₀ + b₀ = W + B ≥ 1 + 1 ≥ 1
(k+1)st time execution reaches inv. point: execution passed while guard/test, so
w_k + b_k > 1 so w_k + b_k ≥ 2
case 1 (bn1.col == white) ∧ (bn2.col == white): w_k+1 + b_k+1 = (w_k - 2) + (b_k+1) = w_k + b_k - 1 ≥ 1
case 2 (bn1.col == black) ∧ (bn2.col == black): exercise
case 3 (else): w_k+1 + b_k+1 = w_k + b_k - 1 = w_k + b_k - 1 ≥ 1

so, by induction, invariant holds each time execution reaches it

2nd invariant

proof of 2nd invariant (by induction) (sketch)

1st time
w₀ = W so w₀ ≡ W (mod 2)

(k+1)st time
assume inv. holds k'th time, so w_k ≡ W (mod 2)

case 1
w_k+1 = w_k - 2 ≡ W - 2 (mod 2) ≡ W (mod 2)

case 2
(exercise)

case 3
w_k+1 = w_k ≡ W (mod 2)

so, by induction, invariant holds each time execution reaches it

variant

variant valid (proof by induction) (sketch)

want to show
variant stays nonneg. and always decreases

1st time
by above, w₀+b₀ ≥ 1 so non-neg.

(k+1)st time
by above, in each case w_k+1 + b_k+1 = w_k + b_k - 1 so variant decreases
execution crossed guard so w_k + b_k ≥ 2 so w_k+1 + b_k+1 ≥ 1

postconditions

loop terminates
variant x+y

w + b = 1
w + b ≥ 1 (last variant) and w + b ≯ 1 (failed guard)

last bean color
white ⇔ W ≅ 1 (mod 2)

another example

while
  w + b > 1
do
  bn1 := removeBean()
  bn2 := removeBean()
  if (bn1.col == black) ∧ (bn2.col == black)
    then putBlack()
  elsif (bn1.col != bn2.col)
    then putWhite()

exercise

assume: b,w start non-negative, body executes t times
describe final b_t,w_t in terms of starting b₀,w₀
hint: possibilities for b_t,w_t are 0,0 0,1 1,0

w₀ is odd ?

b_t,w_t = 0,1

w₀ is even ?

b₀ = 0 ⇒ b_t,w_t = 0,0
b₀ ≥ 1 ∧ w₀ = 0 ⇒ b_t,w_t = 1,0
b₀ ≥ 1 ∧ w₀ ≥ 2 ⇒ b_t,w_t = 0,0 or 1,0 in every case, both are possible (prove this)