computer arithmetic

comp. arith.: psn. num. sys., convert, bin. arith, n-bit reg., 2's-comp.

computer arithmetic

computers use binary arithmetic

positional number systems

binary (2) octal (8) decimal (10) hexadecimal (16: digits 0 … 9 A … F}

positional number systems

decimal (10)

6270310 =
6 × 104 +
2 × 103 +
7 × 102 +
0 × 101 +
3 × 100

binary (2)

1010012 =
1 × 25 +
0 × 24 +
1 × 23 +
0 × 22 +
0 × 21 +
1 × 20

base b

(ad-1ad-2...a1a0)b =
ad-1 × bd-1 +
ad-2 × bd-2 +
. . . +
a1 × b1 +
a0 × b0

convert decimal to base b

repeat: divide by b, take remainder

217 = 2 × 108 + 1
108 = 2 × 54 + 0
54 = 2 × 27 + 0
27 = 2 × 13 + 1
13 = 2 × 6 + 1
6 = 2 × 3 + 0
3 = 2 × 1 + 1
1 = 2 × 0 + 1

21710 = 110110012

check ? convert back (see below)

convert base b to decimal

n <- most sig. digit
while digits remain:
  n <- n*b + next digit
110110012 ?
1 1
1 × 2 + 1 3
3 × 2 + 0 6
6 × 2 + 1 13
13 × 2 + 1 27
27 × 2 + 0 54
54 × 2 + 0 108
108 × 2 + 1 217

check with web calculator:

1 + 2 * (0 + 2 * (0 + 2 * (1 + 2 * (1 + 2 * (0 + 2 * (1 + 2 * (1) ) ) ) ) ) ) = 21710

6253017 ?
6 6
6 × 7 + 2 44
44 × 7 + 5 313
313 × 7 + 3 2194
2194 × 7 + 0 15358
15358 × 7 + 1 107507

1 + 7 * (0 + 7 * (3 + 7 * (5 + 7 * (2 + 7 * (6) ) ) ) ) ) = 10750710

convert binary to hexadecimal

16=24, so start at least sig. bit, group each 4 bits

10100111100110101002 =

101 0011 1100 1101 0100 =

5 3 C D 416

binary arithmetic

use algorithms from elementary school

  1 1  11              00
  1101 0110      1101 0110
+  101 0011    -  101 0011
-----------    -----------
1 0010 1001      1000 0011

                 11010110
               *  1010011
               ----------
                 11010110
                11010110
             11010110
         + 11010110
         ----------------
          100010101100010

              10111
           --------
    1001 | 11010110
           1001
           ----
            1000
            0000
            ----
            10001
             1001
             ----
             10001
              1001
              ----
              10000
               1001
               ----
               0111

n-bit registers

register

  • arithmetic: special-purpose ⇒ small

  • 4-bit: 0000 to 1111 ⇒ 24 numbers

  • 8-bit: 0000 0000 to 1111 1111 ⇒ 28 numbers

  • n-bit: 000…0 to 111…1 ⇒ 2n numbers

  • fixed-size ⇒ can overflow

  • 4-bit: 1101 + 0111 = 0100 ⇒ arith. mod 24

  • 8-bit: 1111 1111 + 0000 0001 = 0000 0000 ⇒ arith. mod 28

  • n-bit: ⇒ arith. mod 2n

neg. numbers: 2's-complement

how to get n-bit pos. and neg. numbers ? (arith mod 2n)

  • -x (mod 2n) = 2n -x (mod 2n)

  • so, pick positive/negative numbers

  • negative: leading bit 1

  • ⇒ negatives: -2n-1 . . . -1

  • ⇒ positives: 1 . . . 2n-1-1

0000      0      0
0001      1      1
0010      2      2
0011      3      3
0100      4      4
0101      5      5
0110      6      6
0111      7      7
1000      8     -8
1001      9     -7
1010     10     -6
1011     11     -5
1100     12     -4
1101     13     -3
1110     14     -2
1111     15     -1
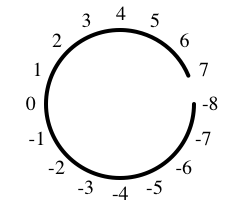
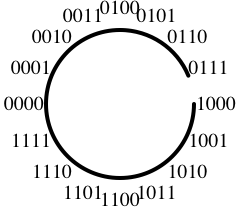
twos complement wheel   wheel bits

2's-complement arithmetic

negate(x)

= 2n – x
= 2n–1 –x + 1
= flip_bits(x) + 1

overflow ?

only if x = –2n-1     (why?)

  neg( 0010 1010 )       neg( 1101 0110 )
   =   1101 0101 + 1      =   0010 1001 + 1
   =   1101 0110          =   0010 1010
x + y

usual method: + (mod 2n)

overflow ?

only if sign(x) = sign(y) ≠ sign(x+y) (why?) 

   1011 1010    1011 0110    1011 0111
 + 1101 1101  + 0101 1101  + 1001 1011
   ---------    ---------    ---------
   1001 0111    0001 0011    0101 0010
x – y

= x + negate(y)