graphs : paths
weighted graphs/digraphs
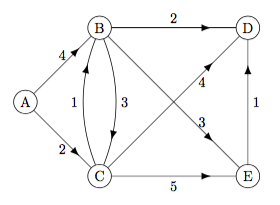
single source shortest path
input: graph/digraph, non-negative edge/arc weights, start node s
output: for each node v, shortest path from s to v
Dijkstra's sssp algorithm
includes proof of correctness

dist parent fringe pick
A B C D E A B C D E -
0 - - - - A - - - - A initialize
A min-dist fringe node
0 4 2 - - A A A - - BC update nbrs
C min-dist fringe node
0 3 2 6 7 A C A C C BDE update nbrs
B min-dist fringe node
0 3 2 5 6 A C A B B DE update nbrs
D min-dist fringe node
0 3 2 5 6 A C A B B E update nbrs
E min-dist fringe node
0 3 2 5 6 A C A B B E update nbrs
dist[s] == 0 fringe = { s }
while not isempty(fringe):
v = a fringe vertex with min dist
remove v from fringe
for each nbr w of v:
add w to fringe (if not there already)
newdist = dist[v] + wt(v,w)
if newdist < dist[w]:
dist[w] = newdist parent[w] = v
def weightSum(G):
sum = 0
for u in G:
for (v,weight) in G[u]: sum += weight
return sum
def showAll(G,D,P):
print '\nprnt',
for v in sorted(G): print P[v],
print '\nnode',
for v in sorted(G): print v,
print '\ndist',
for v in sorted(G): print D[v],
print ''
def showFringe(G,F,D,inf):
print ' fringe',
for v in sorted(F):
if D[v]!=inf:
print v,D[v],' ',
def sssp(G,start):
infinity = 999 + weightSum(G)
dist, parent, fringe = {}, {}, []
for v in G:
dist[v], parent[v] = infinity, -1
fringe.append(v)
dist[start],parent[start] = 0, start
doneEarly = False
while len(fringe)>0 and not doneEarly:
showFringe(G,fringe,dist,infinity)
ndxMin = 0
for j in range(1,len(fringe)):
if dist[fringe[j]] < dist[fringe[ndxMin]]: ndxMin = j
u = fringe.pop(ndxMin)
print '\npick',u,':',
if (dist[u] == infinity): doneEarly = True
for (v,duv) in G[u]:
if dist[v] > dist[u] + duv:
dist[v] = dist[u] + duv
parent[v] = u
print v,dist[v],' ',
print ''
showAll(G,dist,parent)
G = {'A': [['B',4],['C',2]],
'B': [['C',3],['D',2],['E',3]],
'C': [['B',1],['D',4],['E',5]],
'D': [],
'E': [['D',1]]}
sssp(G,'A')
Dijkstra snapshot
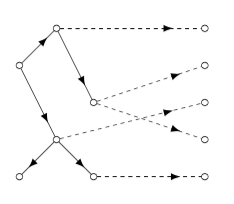
Dijkstra (no priority queue) runtime
n nodes removed from fringe
updating distance values when node v removed from fringe takes Θ(degree v) time
each vertex removed from fringe once, so total Θ(m) time
finding node to remove from fringe takes Θ(k) time, where k is number of nodes in fringe, so total &Theta(n2) time
so total Θ(m + n2) = Θ(n2) time
yes, if we can use priority queue: allows updates and deletemins in o(n2) time
first improvement: implement PQ with binary minheap
better: implement PQ with Fibonacci heap (not in this course)
binary minheap
n nodes, each with key, stored in array H[0 ... n-1]
array represents a complete binary tree
for node H[j]
parent H[ floor( (j-1)/2 ) ]
left child H[ 2*j +1 ]
right child H[ 2*j +2 ]
min-heap property
for each node v with a parent, key(parent(v)) <= key(v)
warning: text uses array indices
H[] is minheap, n is number items in H
trickledown(H,n,j):
while haschild(j) and out-of-order(j, minchild(j)):
newj <- index of smaller child
swap(node(j), node(newj))
j <- newj
bubbleup(H,n,j):
while hasparent(j) and out-of-order(parent(j), j):
newj <- index of parent
swap(node(newj), node(j))
j <- newj
insert(H,n,x):
n <- n+1
H[n] <- x
bubbleup(n)
decreasekey(H,n,j, x):
H[j] <- x
bubbleup(j)
deletemin(H,n):
m <- H[0]
H[0] <- H[n-1]
n <- n-1
trickledown(H,n,0)
buildheap(H,n):
for j in range(n):
H[j] <- new node
bubbleup(j)
buildheapfast(H,n):
for j in range(n): H[j] <- new node
for j in range(0, (n-2)/2, -1): # descending order
trickledown(j)
buildheap time/correctness
for j: 1 .. n-1: bubbleup(j)
array: 4 7 2 1 6 9 5 3 0 8
compact binary tree:
4
7 2
1 6 9 5
3 0 8
bubbleup(1)
4
7 *
* * * *
* * *
bubbleup(2)
2
* 4
* * * *
* * *
bubbleup(3)
1
2 *
7 * * *
* * *
bubbleup(4)
*
2 *
* 6 * *
* * *
bubbleup(5)
*
* 4
* * 9 *
* * *
bubbleup(6)
*
* 4
* * * 5
* * *
bubbleup(7)
*
* *
3 * * *
7 * *
bubbleup(8)
0
1 *
2 * * *
* 3 *
bubbleup(9)
*
* *
* 6 * *
* * 8
minheap
0
1 4
2 6 9 5
7 3 8
array: 0 1 4 2 6 9 5 7 3 8
for j: n/2 .. 0: trickledown(j)
start:
4
7 2
1 6 9 5
3 0 8
trickledown(4)
*
* *
* 6 * *
* * 8
trickledown(3)
*
* *
0 * * *
3 1 *
trickledown(2)
*
* 2
* * 9 5
* * *
trickledown(1)
*
0 *
1 6 * *
3 7 *
trickledown(0)
0
1 2
3 6 * *
4 7 *
minheap
0
1 2
3 6 9 5
4 7 8
array: 0 1 2 3 6 9 5 4 7 8
*
1 1
2 2 2 2
3 3 3 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
bup(1) bup(2) bup(3) … bup(n-1)
worst case: each bup goes to root
wc kc
Σ(j: 2 to n) ⌊ lg j ⌋
∈ Θ(n log n)
(wc kc is 2 times these values)
4
3 3
2 2 2 2
1 1 1 1 1 1 1 1
* * * * * * * * * * * * * * * *
n=3 1 = 3-2
n=7 1+1 +2 = 7-3
n=15 1+1+1+1 +2+2 + 3 = 15-4
n=31 1+1+1+1+1+1+1+1 +2+2+2+2 + 3+3 + 4 = 31-5
n=2^t-1 2^{t-1} + 2(2^{t-2}) + 3(2^{t-3}) + ... + (t-2)(2^1) + (t-1)2^0
sum 1*8 + 2*4 + 3*2 + 4*1 represented by 8A, 8B, 6C, 4D. notice sum is 16+15-5 = 26 * D * C C D * B B B B C C D * A A A A A A A A B B B B C C D *
td(n/2) td(n/2 -1) td(n/2 -3) … td(0)
worst case: each trickledown goes to leaf
simplifying assumption: n = 2k-1
wc kc
2 * ( 1*2k-2 + 2*2k-3 + 3*2k-4 + ... + (k-1)*2k-k )
2k+1 Σ(j: 1 to k-1) j / 2j+1
2k+1 Σ(j: 1 to k-1) j / 2j+1
2k+1 (1 - (k+1)/2k ) = 2(2k - (k+1))
∈ Θ(n)
claim: after bup(j), array[0 1 2 .. j] is a minheap
argue by induction
assume after bup(j-1), array]1 … j-1] is a minheap
now we call bup(j)
case: key[ parent(j) ] ≤ key[ j ]
now every node satisfies the heap property, we are done
case: key[ parent(j) ] > key[ j ]
now we swap these two, and since before the swap key[ parent(j) ] was no greater than the key of any other child, and we have made it smaller, it is still no greater than the key of any other child. continue arguing in this fashion if we bubbleup from parent(j).
2
5 8
8 7 ? *
* * * * * * * *
Dijkstra, with minheap, runtime
trickledown, bubbleup, insert, decreasekey WC Θ(log n)
buildheap WC Θ(n log n)
buildheapfast WC Θ(n)
buildheapfast Θ(n)
n extractmins: Θ(n log n)
m decreasekeys: Θ(m log n)
total Θ((m+n) log n) = Θ(m log n)
with Fibonacci heap, Θ(m + n log n)
negative weights
if neg wt edges and reachable neg wt cycle, then no sssp solution
if neg wt edges but no neg wt cycles, Bellman-Ford solves sssp
def infinity(): return 999
def myprint(d):
if d==infinity(): print '--',
else: print '%2s' % d,
def update(x,y,dxy,D,P):
change = 0
if D[x]<infinity() and D[y] > D[x] + dxy:
D[y], P[y], change = D[x] + dxy, x, 1
return change
def sssp(G,source):
dist, parent = {}, {}
for v in G:
dist[v], parent[v] = infinity(), -1
dist[source],parent[source] = 0, source
print 'from',source,' ',
for v in sorted(G): print '%2s' % v,
print '\ndistance ',
for v in sorted(G): myprint(dist[v])
for _ in range(len(G)-1):
updates = 0
for v in G:
for (w,dvw) in G[v]:
updates += update(v,w,dvw,dist,parent)
print '\ndistance ',
for v in sorted(G): myprint(dist[v])
if updates==0: break
print '\nparent ',
for v in sorted(G): print '%2s' % parent[v],
print ''
G = {'A': [['E',2]],
'B': [['A',1],['C',1]],
'C': [['D',3]],
'D': [['E',-1]],
'E': [['B',-2]],
'F': [['A',-4],['E',-1]],
'G': [['F',1]],
'S': [['A',10],['G',8]]}
sssp(G,'S')