algorithms with numbers

theme

factoring(n): find a prime factor
isprime(n): is n prime ?

logs basic modular gcd isprime genprime RSA

logarithms

logarithm means ‘exponent that gives’
- e.g. logarithm base 2 of n is exponent base 2 that gives n
- exponent x such that 2^x = n
in this course
- lg(x) = lg x is log base 2
- ln(x) = ln x is log base n
- log(x) = log x is log to some undefined base

logs to different bases differ by a constant factor

n = d^lg_dn so …
lg_b n = lg_b d^lg_dn = (lg_b d) (lg_d n), and lg_b d is a constant
e.g. lg₂ n = (lg₂ e) ln n
so Θ(lg₂ n) = Θ(ln n) = Θ(lg₁₇ n) = Θ(log n)

how many bits in binary rep'n of n? 1 + floor( lg(n) ) = Theta( log(n) )

let n positive integer
let k number of bits in binary rep'n of n
in binary
- 1 0 0 . . 0 n smallest 2^k-1
- 1 1 1 . . 1 n largest 2^k-1 < 2^k
2^k-1 ≤ n < 2^k
lg(2^k-1) ≤ lg(n) < lg(2^k)
k-1 ≤ lg(n) < k
lg(n) < k ≤ 1+lg(n)
k = 1 + ⌊ lg(n) ⌋ and k ∈ Θ(lg n)

basic arithmetic

decimal-binary conversion: 206
   1   3   6  12  25  51 103 206
   1   1   0   0   1   1   1   0
decimal -> binary: from right
binary  -> decimal: from left

school addition (binary)
  1     1 1 1     carry
    1 1 0 1 0 1   (53)
  + 1 0 0 0 1 1   (35)
 ---------------
  1 0 1 1 0 0 0   (88)

correctness lemma

In any base at least 2, the sum of any three 1-digit numbers has at most 2 digits.

how long does it take to add two numbers, larger has k bits?

number of bits in sum is k or k+1
school algorithm takes time proportional to number of bits in sum
so school algorithm takes Θ(k) time
can we do better ?
any algorithm takes Ω(k) time to write out answer
so addding two numbers, larger has k bits, takes Θ(k) time

how long does it take to add two numbers, larger is n?

Θ(lg n) bits in n
so addding two numbers, larger is n, takes Θ(lg n) ) time

multiplication

school multiplication (binary)
         1 1 0 1  (13)
      x  1 0 1 1  (11)
-----------------
         1 1 0 1
       1 1 0 1
     0 0 0 0
+  1 1 0 1
-----------------
 1 0 0 0 1 1 1 1  (143)

Al Khwarizmi mult, aka peasant mult
+   13   11
+   26    5
    52    2 (even, omit)
+  104    1
----------
   143

why this works
13 * 11 =  26 * 5.5
        =  26*.5 + 26 * 5
        =  13 +  26 * 5
        =  13 +  52*2.5
        =  13 +  52*.5 + 52*2
        =  13 +  26  + 52 * 2
        =  13 +  26  + 104 * 1
        =  143

recursive mult
def rmult(x,y): # x,y >= 0
  if y==0:
    return 0
  elif 0== y%2:
    return 2*rmult(x, y/2)
  else:
    return x + 2*rmult(x, y/2)

correct ?

claim: for all non-negative integers x,y, rmult(x,y) returns x*y

proof (sketch): induction on y
base case
- assume y=0. then rmult(x,y) returns 0, and x*y=0, done.
inductive case
- let t be a non-negative integer at least 0
- assume claim holds for all y up to and including t
- want to show claim holds for y = t+1
- case 0: assume t even, say t = 2*j
- so t+1 = 2*j+1 is odd, and (t+1)/2 = j
- so rmult(x,t+1) returns x+2*rmult(x,(t+1)/2) = x+2*rmult(x, j)
- = x+2*(x*j) by induction hypothesis, since j non-neg and at most t
- = x*(2j+1) = x*(t+1), so claim holds in this case.
- case 1: assume t odd. exercise.
QED

runtime ?

assume x,y each have k bits
with each call, number of bits of y-parameter decreases by 1
so 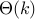calls
each call is either shift (multiply by 2), at most 2k bits
also might have add (at most k-bits)
so each call
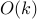
total time

exercise

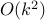
how long to multiply 2 k-bit numbers with school algorithm?}

how long does it take to multiply?

unless otherwise specified, assume that we want to answer as a function of the size of the input
so, what is the size of the input?
unless otherwise specified, this is the space need to represent the input
so here, this would be the number of bits needed to represent the two numbers
answer: 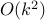time, where k is the number of bits needed to store the input
why do I not write 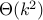here?

can we do better ?

yes (later)

recursive div: motivation
= q * 13 + r  ?
50  25  12  6  3  1  0
= 0 * 13 + 0
= 0 * 13 + 1    <--2*0+1
= 0 * 13 + 3    <--2*1+1
= 0 * 13 + 6    <--2*3
= 0 * 13 + 12   ...
= 0 * 13 + 25
    = 1 * 13 + (25-13) <-- 12
= 2 * 13 + 24
    = 3 * 13 + (24-13) <-- 11
= 6 * 13 + 22
    = 7 * 13 + (22-13) <-- 9

recursive div
def rdiv(x,y): # y >= 1, x >= 0
  print 'rdiv(',x,y,')'
  if x==0:
    return 0,0
  q,r = rdiv(x/2,y)
  q,r = 2*q, 2*r
  if 1==x%2:
    r = r+1
  if r >= y:
    q,r = q+1, r-y
  print x,'=',q,'*',y,'+',r
  return q,r

rdiv( 100 13 )
rdiv( 50 13 )
rdiv( 25 13 )
rdiv( 12 13 )
rdiv( 6 13 )
rdiv( 3 13 )
rdiv( 1 13 )
rdiv( 0 13 )
1 = 0 * 13 + 1
3 = 0 * 13 + 3
6 = 0 * 13 + 6
12 = 0 * 13 + 12
25 = 1 * 13 + 12
50 = 3 * 13 + 11
100 = 7 * 13 + 9

recursive div

correct ?
runtime ? 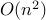, where 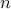is the number of bits in x,y
can we do better ?

modular arithmetic

x (mod n)

for integer n > 1, x (mod n) is the remainder upon division of x by n:
integer r s.t. x = qn + r, where 0 ≤ r < n
x ≡ y (mod n) iff exists k, x-y = kn
if x ≡ x' (mod n) and y ≡ y' (mod n), then
- x + y ≡ x' + y' (mod n)
- x - y ≡ x' - y' (mod n)
- x - y ≡ x' - y' (mod n)
consequence: can do modular arithmetic so that numbers stay small

113 * (167 + 484) + 192 * 145  (mod 21)
113 * (167 + 484) + 192 * 145  (mod 21) =
113 * (   651   ) + 192 * 145  (mod 21) =
113 * (   651   ) +   27840    (mod 21) =
   73563          +   27840    (mod 21) =
                101403         (mod 21) =
                  15           (mod 21)
instead:

113 * (167 + 484) + 192 * 145  (mod 21) =
 8  * (-1  +  1 ) +  3  * (-2) (mod 21) =
    0             +    -6      (mod 21) =
                  15           (mod 21)

modular exponentiation
def modexp(x,y,n): #integers, y >= 0, n >= 2
  if y==0:
    return 1
  z = modexp(x,y/2,n)
  if 0==y%2:
    return (z*z)%n
  else:
    return (x*z*z)%n

for j in range(-5,5):
  for k in range(10):
    for m in range(10):
      assert modexp(j,k,m+2)==pow(j,k,m+2)

mod exp

correct ?
runtime ? 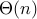calls, mult'n, so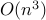
better ?

Euclid's gcd

history

Euclid circa 325-265 BC (?)
Elements VII.2
improvement: a%b instead of a-b
today: inverse (mod n): primality testing, RSA

Euclid gcd
def euclid(a,b): # a >= b >= 0
  print a,
  while b>0:
    a, b = b, a % b
    print a,
  print ''
  return a

euclid(9873,3627)
  9873 3627 2619 1008 603 405 198 9
euclid(144,89)
  144 89 55 34 21 13 8 5 3 2 1

correctness: gcd(a,b) = gcd(b, a-b)

assume x divides a, x divides b
- so exists j, x*j = a
- so exists k, x*k = b
- so a-b = x*(j-k)
- so exists m, x*m = a-b
- so x divides a-b
so { common divisors a,b } subset of { common divisors b,a-b }
similarly, { common divisors b,a-b } subset of { common divisors a,b }
so … QED

corollary: gcd(a,b) = gcd(b, a%b)

euclid(a,b) returns gcd(a,b)

prove by induction on b
- after each iteration
  - gcd(a,b) = gcd(a.prev, b.prev)
  - 0 ≤ b < b.prev

complexity: for a at least b, a mod b less than a/2

case b ≤ a/2: a mod b < b ≤ a/2
case b > a/2: a mod b = a - b < a/2

corollary: two consecutive rounds halves a,b, so ≤ 2 lg(b) iterations

corollary: number iterations in O( lg(b) )

complexity: at most 1.44.. lg(b) iterations, and this can happen

proof: Lame 1844, induction
smallest b causing n iterations is Fibonacci(n)
so ≤ lg(b) / lg(1.618…) iterations, and
- Fib sequence gives this many iterations
corollary: worst case iterations in Theta( lg(b) )

euclid gcd

correct ? above
runtime ?
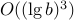
can we do better ?

linear combo lemma

integers a,b,x,y,d: d > 0 d | a d | b d = ax + by then
d = gcd(a,b)

proof:

every common divisor of a,b divides every linear combination of a,b
every common divisor of a,b ≤ every postive linear combo of a,b
every common divisor of a,b ≤ d, so gcd(a,b) ≤ d
d | a,b, so d common divisor of a,b, so d ≤ gcd(a,b)

example
7 > 0
7 | 135716                           (?)
7 | 8616909                          (?)
8616909 * -321 + 135716 * 20381 = 7  (?)
so 7 = gcd(8616909,135716)

extended euclid gcd: find x,y s.t. ax+by=gcd(a,b)
def exteuclid(a,b): #a>=b>=0: x,y,d: ax+by=d=gcd(a,b)
  if b==0:
    print a,'* 1 +',b,'* 0 =',a
    return 1, 0, a
  x, y, d = exteuclid(b, a%b)
  print a,'*',y,'+',b,'*',x-(a/b)*y,'=',d
  return y, x-(a/b)*y, d

exteuclid(8616909,135716)
  7 * 1 + 0 * 0 = 7
  420 * 0 + 7 * 1 = 7
  847 * 1 + 420 * -2 = 7
  1267 * -2 + 847 * 3 = 7
  2114 * 3 + 1267 * -5 = 7
  66801 * -5 + 2114 * 158 = 7
  135716 * 158 + 66801 * -321 = 7
  8616909 * -321 + 135716 * 20381 = 7

extended euclid gcd

correct ?
runtime ?
can we do better ?

modular division

x is multiplicative inverse of a mod n if ax ≡ 1 (mod n)

a has mult. inv. mod n iff gcd(a,n) = 1, in which case use ext.euc. to find it

examples using extended Euclid gcd

find 193^-1 (mod 905)
193*347 + 905*-74 = 1, so
193^-1 (mod 905) = 347
find 39^-1 (mod 60)
60*2 + 39*-3 = 3, so
39^-1 (mod 60) does not exist
find 23^-1 (mod 37)
37*5 + 23*-8 = 1, so
23^-1 (mod 37) = -8 = 29

primality

one of these two numbers is probably prime

9807557252 8648173575 5038095692 9736165065 8570516592 8591379633

1 0545319355 9649383033 0184689288 7085596360 3199992904 9022641801

simple
def isprime(n):
  for j in range(2,n):
    if 0==n%j:
      return False  # composite
  return True      # prime

for t in range(2, 1000):
  if isprime(t):
    print t

correct ?
runtime? worst case Θ(n (log n)²)
runtime? exponential in size of input
- assume numbers stored in binary
- size of input is k = Θ(lg n)
- runtime? worst case Θ(2^k k²)
can we do better?

theorems

p prime, a ∈ [1 ... p-1] ⇒
- a^p-1 = 1 (mod p) Fermat a^j (mod p)
- a² = 1 (mod p) ⇒ a = ± 1 (mod p) Euclid

corollaries

n composite if exists a ∈ [2 ... n-2] s.t.
- a^n-1 ≠ 1 (mod n) (Fermat) or
- a² = 1 (mod n) (Euclid, nontrivial square root of 1)

composite witness examples

is 561 prime ?
- notice 396⁵⁶⁰ (mod 561) = 528
- so 396 is Fermat witness that 561 is composite
is 8911 prime ?
- notice 6698² (mod 8911) = 1
- so 396 is Euclid witness that 8911 is composite

efficient computation of 396^560 (mod 561)
560 280 140 70 35 17 8 4 2 1
a^1 = 396 (mod 561)
a^2 = (a^1)^2 = 396*396 = 297 (mod 561)
a^4 = (a^2)^2 = 297*297 = 132 (mod 561)
a^8 = (a^4)^2 = 132*132 =  33 (mod 561)
a^17 = a*(a^8)^2 = 396*33*33 = 396 (mod 561)
a^35 = a*(a^17)^2 = 396*(396*396) = 363 (mod 561)
a^70 = (a^35)^2 = 495 (mod 561)
a^140 = (a^70)^2 = 429 (mod 561)
a^280 = (a^140)^2 = 33 (mod 561)
a^560 = (a^280)^2 = 528 (mod 561)

Miller Rabin probabilistic primality test

repeat k times
- pick random a ∈ [2 ... n-2]
- compute a^n-1 (mod n), at same time look for nontrivial root
- if a^n-1 ≠ 1 (mod n) or nontrivial root found:
  - return composite
return probably prime

Miller Rabin success probability

one-sided error
if witness found, then n composite
if no witness found, then n probably prime
- if n composite, then at least 3/4 of [2 .. n-2] are witnesses
- Probability(false positive) = Prob(n composite but no witness found) ≤ 1/4^k
- e.g. k = 10, Prob(false positive) ≤ 1/4¹⁰ < 1e-6
- e.g. k = 20, Prob(false positive) < 1e-12

miller rabin examples: n = 561
z = 560 280 140 70 35
a = 12
a^35          (mod 561) =  45
a^70  =  45^2 (mod 561) = 342
a^140 = 342^2 (mod 561) = 276
a^280 = 276^2 (mod 561) = 441
a^560 = 441^2 (mod 561) = 375  <= not 1, report composite

a = 101
a^35          (mod 561) = 560  = -1 :(
a^70  = 560^2 (mod 561) =   1
a^140 =   1^2 (mod 561) =   1
a^280 =   1^2 (mod 561) =   1
a^560 =   1^2 (mod 561) =   1    (if only this a, report prob prime)

a = 29
a^35          (mod 561) = 164
a^70  = 164^2 (mod 561) = 529
a^140 = 529^2 (mod 561) = 463
a^280 = 463^2 (mod 561) =  67
a^560 =  67^2 (mod 561) =   1  <= 67^2 = 1, report composite

miller rabin
def compositeWitness(w,n,verbose): # miller rabin
  # is w witness for n composite ?
  assert 1==n%2
  s,z = 0, n-1
  while (0== z%2):
    s+=1
    z/=2
  y = pow(w,z,n)
  for j in range(s):
    z = (y*y)%n
    if z == 1 and y !=1 and y != n-1:
      if verbose: print w, 'yields root', y
      return True  # yes, composite
    y = z
  if (z != 1):
    if verbose: print w, '  fails Fermat'
    return True    # yes, composite
  return False       # no, probably prime

def isComposite(n,t,verbose): # t tries to show composite
  if verbose: print n,
  knownComposite = False
  tries = 0
  while (not knownComposite) and (tries < t):
    tries += 1
    a = random.randint(2,n-2)
    knownComposite = compositeWitness(a,n,verbose)
    if verbose and not knownComposite: print a,
  return knownComposite

def primetest(n,t):
  if isComposite(n,t,False):
    print n,'composite'
  else:
    print n,'prime\nProb >= 1.0 -', pow(.25,t)

which number is prime?
x = 980755725286481735755038095692973616506585705165928591379633
y = 1054531935596493830330184689288708559636031999929049022641801
primetest(x,5)
primetest(y,5)
primetest(x,200)

AKS primality test

generating primes

cryptography: need primes several hundred bits long

Lagrange etc

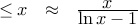
the number of primes $leq x : : : approx ::: frac{displaystyle x}{displaystyleln x - 1}$
corollary: prob(number with at most 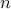-bits is prime)
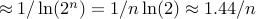
so on average 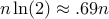picks suffice to find 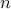-bit prime
e.g. prob(number with at most 33-bits is prime) 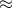1.44/33 = .043
average number of picks to find 33-bit prime 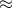23
1/2 as many picks if you skip even numbers
1/6 as many picks if you skip numbers divisible by 2 or 3
etc.

miller-rabin prime generation
def primegen(n,t,verbose): # find n-bit probable-prime
  found = False
  low, high = pow(2,n-2), pow(2,n-1)-1
  attempts = 0
  while not found:
    attempts += 1
    a = 2*random.randint(low,high)+1
    if verbose: print a
    found = not isComposite(a,t,verbose)
  if verbose: print attempts, 'attempts'
  return a, attempts  # Prob(a prime) >= 1 - (1/4)^t

numbits, experiments, sum = 100, 100, 0
for j in range(experiments):
  sum += primegen(numbits,20,False)[1]
print 'avg trials to find prime', sum/(experiments*1.0)
print 'expected number of trials', math.log(pow(2,numbits))/2.0