# jemdoc: addcss{rbh.css}, addcss{jacob.css}
= p vs np
~~~
{}{raw}
history
P
NP
NP-C
sat
21 others
sat->3sat
3sat->IS
longest path
clique
wc time
~~~
~~~
{}{raw}
complexity theory: history
~~~
~~~
- [http://aleph0.clarku.edu/~djoyce/hilbert/ 1900 Hilbert 23 problems]
- [https://en.wikipedia.org/wiki/Millennium_Prize_Problems 2000 Clay 7 problems]
- [https://simple.wikipedia.org/wiki/P_versus_NP P = NP? simple.wiki]
- [https://en.wikipedia.org/wiki/Bombe Turing et al Bombe]
- [https://en.wikipedia.org/wiki/Colossus_computer Colossus]
- [https://en.wikipedia.org/wiki/ENIAC ENIAC]
- [https://en.wikipedia.org/wiki/Blossom_algorithm blossoms]
- [http://www.math.uiuc.edu/documenta/vol-ismp/34_pulleyblank-william.pdf good algorithm]
~~~
~~~
{}{raw}
class P
~~~
~~~
- decision problem: answer yes or no
-- e.g. here is a graph, is there a path between A,B with distance at most 31?
-- e.g. here is a graph, does it have a clique of size 32?
-- e.g. here is a CNF formula, is it satisfiable?
- class P: set of decision problems that can be solved in polytime
-- e.g. at-most-k distance problem: given a graph G, nodes A,B, integer k,
is there a path between A,B with distance at most k?
-- (how does this differ from the shortest path problem?)
- not known:
-- k-clique in P ?
-- sat (satisfiability) in P ?
~~~
~~~
{}{raw}
class NP
~~~
~~~
- decision problem yes(no)-instance: instance of problem where answer is yes(no)
- class NP
-- decision problem
-- for every yes-instance, exists yes-proof (proof that answer is yes)
that can be verified in polytime
- e.g. is sat in NP ?
-- yes, because
-- consider a yes instance, i.e. a satisfiable formula
-- it must have a satisfying assignment
-- so a yes-proof for sat is a satisfying assignment
-- if someone gives you a formula in CNF, and an assignment, how long does it take you to verify that this assignment satisfies the formula?
-- you assign truth values to the n variables, time O(n)
-- for each clause, you check that the assignment is satisfied, time O(nm)
-- so in O(nm) time you can verify that the formula is satisfiable
-- so sat is in NP
~~~
~~~
{}{raw}
class NP-C
~~~
~~~
- class NP-C: NP-complete problems
-- informally, each problem in NP-C is as hard as any problem in NP
-- formally, a problem X in NP is +complete+ if, for each problem A in NP,
there is a polytime process that
--- takes an instance a of A
--- converts it into an instance x of X
--- preserves yes-answers: answer(a) is yes if and only if answer(x) is yes
- consequence
-- suppose exists polytime algorithm for some such X
-- then any problem in NP can be solved in polytime
- above consequence is why we say NP-C are hardest problems in NP
~~~
~~~
{}{raw}
sat NP-C
~~~
~~~
- 1971 (Cook) CNF-sat is NP-complete.
- [https://en.wikipedia.org/wiki/Cook-Levin_theorem Cook-Levine theorem and proof]
- unrestricted sat is a generalization of CNF-sat, and also in NP,
so unrestricted sat is also NP-complete
- transform from sat to cnf-sat with [https://en.wikipedia.org/wiki/Conjunctive_normal_form Tseitin's method]
- transform from cnf-sat to 3-sat (at most 3, or exact 3) [https://cse.iitkgp.ac.in/~palash/2018AlgoDesignAnalysis/SAT-3SAT.pdf like this]
- transform from exact-3-sat to 3-coloring
[https://cgi.csc.liv.ac.uk/~igor/COMP309/3CP.pdf like this]
~~~
~~~
{}{raw}
21 others NP-C
~~~
~~~
- suppose we want to show problem X is NP-complete (so, hard)
- what can we do ?
-- 1) show X is in NP
-- 2) show that some NP-complete problem C can be poly-transformed into X,
so that answers (yes/no) are same for C instance and transformed X instance
-- 3) then we have shown X is NP-complete. why ?
-- because any problem T in NP can be transformed into sat, and then into X
-- so if we could solve X in poly T, we could solve T in poly time
- 1972 (Karp) 21 problems NP-C:
-- 3-sat (each clause has {{≤}} 3 literals)
-- clique
-- knapsack
-- set cover
-- {{...}}
- [https://en.wikipedia.org/wiki/Karp%27s_21_NP-complete_problems Karp's 21 reductions]
~~~
~~~
{}{raw}
sat reduces to 3-sat
~~~
~~~
{example reduction}{}
consider an instance of sat:
[ 1 2 3 -4 -6 ]
[ 1 2 -3 -5 ]
[ 1 -2 3 -5 -6 ]
[ 1 3 4 ]
[ 2 -3 4 -6 ]
replace each long clause with
equivalent set of 3-literal clauses
[ 1 2 3 -4 -6] => [ 1 2 10] [-10 3 11] [-11 -4 -6]
[ 1 2 -3 -5] => [ 1 2 12] [-12 -3 -5]
[ 1 -2 3 -5 -6] => [ 1 -2 13] [-13 3 14] [-14 -5 -6]
[ 2 -3 4 -6] => [ 2 -3 15] [-15 4 -6]
corresponding instance of 3-sat
[ 1 2 10 ]
[ -10 3 11 ]
[ -11 -4 -6 ]
[ 1 2 12 ]
[ -12 -3 -5 ]
[ 1 -2 13 ]
[ -13 3 14 ]
[ -14 -5 -6 ]
[ 1 3 4 ]
[ 2 -3 15 ]
[ -15 4 -6 ]
~~~
~~~
{above reduction implies 3-sat is NP-C}
- number literals in new instance < 3 times original, so reduction polytime
- reduction maps yes-instance to yes-intance, no-instance to no-instance
- by Cook's theorem
-- sat is NP-C
-- so any instance t of problem T in NP can be polytime reduced to instance s of sat, with answer preserved
- as above, instance s can be polytime reduced to instance u of 3-sat, with
answer preserved
- so t can be polytime reduced to u, with answer preserved
- so polysolving 3-sat implies polysolving T, for every T in NP
- so 3-sat is NP-complete
~~~
~~~
{clique and independent set}
- [https://en.wikipedia.org/wiki/Clique_(graph_theory) clique] in a graph, set of nodes, each pair adjacent
- [https://en.wikipedia.org/wiki/Independent_set_(graph_theory) independent set] in a graph, set of nodes, each pair non-adjacent
- independent set decision problem: given a graph G and an integer k, does G have an independent set of size k ?
- clique decision problem: given a graph G and an integer k, does G have a clique of size k ?
~~~
~~~
{}{raw}
3-sat reduces to ind. set
~~~
~~~
{example reduction}
- consider an instance of 3-sat
- each clause with t literals becomes clique with t nodes
- e.g. clause {{[ a b -c ]}} becomes clique \{a b -c\}
- for each literal pair x,-x from different clauses, add edge in graph
- e.g. what is graph reduced from this CNF formula?
{{[-1 2 -3] [ 1 -2 3] [ 1 2 3] [-1 2]}}
~~~
~~~
{}
{{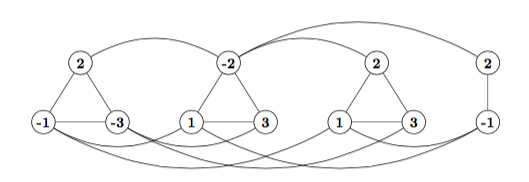 }}
~~~
~~~
{claim: formula satisfiable iff graph has m-independent set}
- assume formula satisfiable, say with assignment A
-- in each clause, at least one literal true
-- in graph, pick one true node from each clause
-- picked nodes form independent set (why?)
-- so graph has m-ind set
- assume graph has m-ind set
-- set has exactly one node in each clauseclique
-- set corresponding literal true
-- cannot have both x and -x true (why?)
-- each clause satisfied by this assignment
~~~
~~~
{consequence of claim ?}
- independent set is NP-C :)
- why ?
~~~
~~~
{exercise}
show independent set reduces to clique
~~~
~~~
{consequence of exercise ?}
- clique is NP-C :)
- why ?
~~~
~~~
{}{raw}
}}
~~~
~~~
{claim: formula satisfiable iff graph has m-independent set}
- assume formula satisfiable, say with assignment A
-- in each clause, at least one literal true
-- in graph, pick one true node from each clause
-- picked nodes form independent set (why?)
-- so graph has m-ind set
- assume graph has m-ind set
-- set has exactly one node in each clauseclique
-- set corresponding literal true
-- cannot have both x and -x true (why?)
-- each clause satisfied by this assignment
~~~
~~~
{consequence of claim ?}
- independent set is NP-C :)
- why ?
~~~
~~~
{exercise}
show independent set reduces to clique
~~~
~~~
{consequence of exercise ?}
- clique is NP-C :)
- why ?
~~~
~~~
{}{raw}
longest path
~~~
~~~
- *longest path* ~ given graph G, find a longest path
- how hard is longest path ?
- longest path not in NP (not a yes/no question)
- decision version of longest path ?
- *k-path* ~ given graph G and integer k, does G have path with {{≥ k}} nodes?
- *Hamiltonian path* ~ given graph G, does G have path with all nodes?
- *Hamiltonian cycle* ~ given graph G, does G have cycle with all nodes?
- H-cycle is in NP-C: Karp's reduction from
[http://cs.indstate.edu/~bdhome/HamCycle.pdf vertex cover]
- can you prove that H-path is NP-C ?
- proof: reduction from H-cycle. ~
let G be input to H-cycle. ~
for each edge (x,y) of G, construct graph G(x,y) as follows:
-- remove edge (x,y)
-- add new node w, adjacent only to x
-- add new node z, adjacent only to y
- claim: G has H-cycle through edge (x,y) iff G(x,y) has H-path
- so G has H-cycle iff at least one G(x,y) has H-path
- so assume H-path is in P
- use some such alg on each graph G(x,y)
- so, in this way,
if we can solve H-path in time {{O(nt)}} for fixed t,
we can solve H-cycle in time {{O(nt+2)}}
- so we have proved that H-path is in NP-C
- this {{H-cycle->H-path}} reduction,
with multiple calls to the target algorithm,
is called a *Cook* reduction
- other reductions we have seen, with 1 call to target algorithm,
are called *Karp* reductions
- a problem is *NP-hard* if it is as hard as some NP-C problem, but not
necessarily in NP
- longest path is NP-hard
~~~
~~~
{}{raw}
brute force k-clique time
~~~
~~~
- try each k-subset
-- (n choose k) = ${\Large\mathbf{n \choose k}}$ {{= n! / (k!) (n-k)! = n(n-1)...(n-(k-1)) / k!}} subsets
-- checking each takes {{Θ(k2)}} time
- if k constant, {{Θ(nk)}} subsets,
total WC time {{Θ(k2 nk) = Θ(nk) }} polynomial :)
- here, WC time polynomial :)
- if k not constant, e.g. can grow with n ?
-- largest (n choose k) ? when {{k = n/2}} (CMPUT 272)
-- how big is (n choose n/2) ?
-- {{ n! ≈
√
2 π n
(n/e)n }} (Stirling)
-- better: {{4^n/(sqrt(pi*(n+1/3))) <= (2n choose n) <= 4^n/(sqrt(pi*(n+1/4)))}}
-- so (n choose n/2) grows
--- slower than {{2^n}}
--- faster than {{(2-eps)^n}}, for any positive epsilon
- try each subset, worst case runtime {{Θ( n1.5 2n )}}
- here, WC time exponential :(
~~~
~~~
{1000 choose 500}{}
2.7035582144 e+299 Stirling approx
2.7028824093 e+299 better "
2.7028824095 e+299 exact (rounded)
~~~
~~~
{}{raw}
wc time for some NP-C problems
~~~
~~~
- brute force clique, also independent set
-- {{Θ( n1.5 2n )}}
- knapsack, n items, each value/wt n bits, capacity .5 total wt, input size {{t = Θ( n2 )}}
-- {{Θ( n2 2n ) = Θ( t 2√ t )}}
- brute force set cover, m subsets of an n-set
-- {{Θ( n 2m )}}
- brute force sat, total m literals, n variables
-- {{Θ( m 2n )}}
~~~
 }}
~~~
~~~
{claim: formula satisfiable iff graph has m-independent set}
- assume formula satisfiable, say with assignment A
-- in each clause, at least one literal true
-- in graph, pick one true node from each clause
-- picked nodes form independent set (why?)
-- so graph has m-ind set
- assume graph has m-ind set
-- set has exactly one node in each clauseclique
-- set corresponding literal true
-- cannot have both x and -x true (why?)
-- each clause satisfied by this assignment
~~~
~~~
{consequence of claim ?}
- independent set is NP-C :)
- why ?
~~~
~~~
{exercise}
show independent set reduces to clique
~~~
~~~
{consequence of exercise ?}
- clique is NP-C :)
- why ?
~~~
~~~
{}{raw}
}}
~~~
~~~
{claim: formula satisfiable iff graph has m-independent set}
- assume formula satisfiable, say with assignment A
-- in each clause, at least one literal true
-- in graph, pick one true node from each clause
-- picked nodes form independent set (why?)
-- so graph has m-ind set
- assume graph has m-ind set
-- set has exactly one node in each clauseclique
-- set corresponding literal true
-- cannot have both x and -x true (why?)
-- each clause satisfied by this assignment
~~~
~~~
{consequence of claim ?}
- independent set is NP-C :)
- why ?
~~~
~~~
{exercise}
show independent set reduces to clique
~~~
~~~
{consequence of exercise ?}
- clique is NP-C :)
- why ?
~~~
~~~
{}{raw}