p vs np
complexity theory: history
class P
decision problem: answer yes or no
e.g. here is a graph, is there a path between A,B with distance at most 31?
e.g. here is a graph, does it have a clique of size 32?
e.g. here is a CNF formula, is it satisfiable?
class P: set of decision problems that can be solved in polytime
e.g. at-most-k distance problem: given a graph G, nodes A,B, integer k, is there a path between A,B with distance at most k?
(how does this differ from the shortest path problem?)
not known:
k-clique in P ?
sat (satisfiability) in P ?
class NP
decision problem yes(no)-instance: instance of problem where answer is yes(no)
class NP
decision problem
for every yes-instance, exists yes-proof (proof that answer is yes) that can be verified in polytime
e.g. is sat in NP ?
yes, because
consider a yes instance, i.e. a satisfiable formula
it must have a satisfying assignment
so a yes-proof for sat is a satisfying assignment
if someone gives you a formula in CNF, and an assignment, how long does it take you to verify that this assignment satisfies the formula?
you assign truth values to the n variables, time O(n)
for each clause, you check that the assignment is satisfied, time O(nm)
so in O(nm) time you can verify that the formula is satisfiable
so sat is in NP
class NP-C
class NP-C: NP-complete problems
informally, each problem in NP-C is as hard as any problem in NP
formally, a problem X in NP is complete if, for each problem A in NP, there is a polytime process that
takes an instance a of A
converts it into an instance x of X
preserves yes-answers: answer(a) is yes if and only if answer(x) is yes
consequence
suppose exists polytime algorithm for some such X
then any problem in NP can be solved in polytime
above consequence is why we say NP-C are hardest problems in NP
sat NP-C
1971 (Cook) CNF-sat is NP-complete.
unrestricted sat is a generalization of CNF-sat, and also in NP, so unrestricted sat is also NP-complete
transform from sat to cnf-sat with Tseitin's method
transform from cnf-sat to 3-sat (at most 3, or exact 3) like this
transform from exact-3-sat to 3-coloring like this
21 others NP-C
suppose we want to show problem X is NP-complete (so, hard)
what can we do ?
1) show X is in NP
2) show that some NP-complete problem C can be poly-transformed into X, so that answers (yes/no) are same for C instance and transformed X instance
3) then we have shown X is NP-complete. why ?
because any problem T in NP can be transformed into sat, and then into X
so if we could solve X in poly T, we could solve T in poly time
1972 (Karp) 21 problems NP-C:
3-sat (each clause has ≤ 3 literals)
clique
knapsack
set cover
...
sat reduces to 3-sat
consider an instance of sat: [ 1 2 3 -4 -6 ] [ 1 2 -3 -5 ] [ 1 -2 3 -5 -6 ] [ 1 3 4 ] [ 2 -3 4 -6 ] replace each long clause with equivalent set of 3-literal clauses [ 1 2 3 -4 -6] => [ 1 2 10] [-10 3 11] [-11 -4 -6] [ 1 2 -3 -5] => [ 1 2 12] [-12 -3 -5] [ 1 -2 3 -5 -6] => [ 1 -2 13] [-13 3 14] [-14 -5 -6] [ 2 -3 4 -6] => [ 2 -3 15] [-15 4 -6] corresponding instance of 3-sat [ 1 2 10 ] [ -10 3 11 ] [ -11 -4 -6 ] [ 1 2 12 ] [ -12 -3 -5 ] [ 1 -2 13 ] [ -13 3 14 ] [ -14 -5 -6 ] [ 1 3 4 ] [ 2 -3 15 ] [ -15 4 -6 ]
number literals in new instance < 3 times original, so reduction polytime
reduction maps yes-instance to yes-intance, no-instance to no-instance
by Cook's theorem
sat is NP-C
so any instance t of problem T in NP can be polytime reduced to instance s of sat, with answer preserved
as above, instance s can be polytime reduced to instance u of 3-sat, with answer preserved
so t can be polytime reduced to u, with answer preserved
so polysolving 3-sat implies polysolving T, for every T in NP
so 3-sat is NP-complete
clique in a graph, set of nodes, each pair adjacent
independent set in a graph, set of nodes, each pair non-adjacent
independent set decision problem: given a graph G and an integer k, does G have an independent set of size k ?
clique decision problem: given a graph G and an integer k, does G have a clique of size k ?
3-sat reduces to ind. set
consider an instance of 3-sat
each clause with t literals becomes clique with t nodes
e.g. clause [ a b -c ] becomes clique {a b -c}
for each literal pair x,-x from different clauses, add edge in graph
e.g. what is graph reduced from this CNF formula?
[-1 2 -3] [ 1 -2 3] [ 1 2 3] [-1 2]
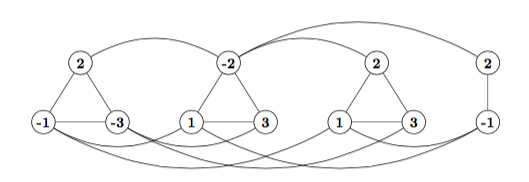
assume formula satisfiable, say with assignment A
in each clause, at least one literal true
in graph, pick one true node from each clause
picked nodes form independent set (why?)
so graph has m-ind set
assume graph has m-ind set
set has exactly one node in each clauseclique
set corresponding literal true
cannot have both x and -x true (why?)
each clause satisfied by this assignment
independent set is NP-C :)
why ?
show independent set reduces to clique
clique is NP-C :)
why ?
longest path
longest path given graph G, find a longest path
how hard is longest path ?
longest path not in NP (not a yes/no question)
decision version of longest path ?
k-path given graph G and integer k, does G have path with ≥ k nodes?
Hamiltonian path given graph G, does G have path with all nodes?
Hamiltonian cycle given graph G, does G have cycle with all nodes?
H-cycle is in NP-C: Karp's reduction from vertex cover
can you prove that H-path is NP-C ?
proof: reduction from H-cycle. let G be input to H-cycle. for each edge (x,y) of G, construct graph G(x,y) as follows:
remove edge (x,y)
add new node w, adjacent only to x
add new node z, adjacent only to y
claim: G has H-cycle through edge (x,y) iff G(x,y) has H-path
so G has H-cycle iff at least one G(x,y) has H-path
so assume H-path is in P
use some such alg on each graph G(x,y)
so, in this way, if we can solve H-path in time O(nt) for fixed t, we can solve H-cycle in time O(nt+2)
so we have proved that H-path is in NP-C
this H-cycle->H-path reduction, with multiple calls to the target algorithm, is called a Cook reduction
other reductions we have seen, with 1 call to target algorithm, are called Karp reductions
a problem is NP-hard if it is as hard as some NP-C problem, but not necessarily in NP
longest path is NP-hard
brute force k-clique time
try each k-subset
(n choose k) =
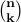= n! / (k!) (n-k)! = n(n-1)...(n-(k-1)) / k! subsetschecking each takes Θ(k2) time
if k constant, Θ(nk) subsets, total WC time Θ(k2 nk) = Θ(nk) polynomial :)
here, WC time polynomial :)
if k not constant, e.g. can grow with n ?
largest (n choose k) ? when k = n/2 (CMPUT 272)
how big is (n choose n/2) ?
n! ≈ √ 2 π n (n/e)n (Stirling)
better: 4^n/(sqrt(pi*(n+1/3))) <= (2n choose n) <= 4^n/(sqrt(pi*(n+1/4)))
so (n choose n/2) grows
slower than 2^n
faster than (2-eps)^n, for any positive epsilon
try each subset, worst case runtime Θ( n1.5 2n )
here, WC time exponential :(
2.7035582144 e+299 Stirling approx 2.7028824093 e+299 better " 2.7028824095 e+299 exact (rounded)
wc time for some NP-C problems
brute force clique, also independent set
Θ( n1.5 2n )
knapsack, n items, each value/wt n bits, capacity .5 total wt, input size t = Θ( n2 )
Θ( n2 2n ) = Θ( t 2√ t )
brute force set cover, m subsets of an n-set
Θ( n 2m )
brute force sat, total m literals, n variables
Θ( m 2n )