graphs: decompositions

rep'n dfs components runtime bfs digraph scc

a graph
D     A -- C  B -- H
      | \  |    \  |
      |  \ |     \ |
      E -- F       G

nodes   A B C D E F G H
degrees 3 2 2 0 2 3 2 2
edges  8
sum of degrees 16

graph lingo

wiki
G = (V,E)
graph, vertex/node/point, edge/line
adjacent
subgraph
connected
component: maximal connected subgraph
degree of a vertex
n or |V| number of nodes
m or |E| number of edges

graph representation

two ways to represent a graph
adjacency matrix

    A  B  C  D  E  F  G  H
A   0  0  1  0  1  1  0  0
B   0  0  0  0  0  0  1  1
C   1  0  0  0  0  1  0  0
D   0  0  0  0  0  0  0  0
E   1  0  0  0  0  1  0  0
F   1  0  1  0  1  0  0  0
G   0  1  0  0  0  0  0  1
H   0  1  0  0  0  0  1  0

adjacency list

      A   [C E F]
      B   [H G]
      C   [A F]
      D   [ ]
      E   [A F]
      F   [A C E]
      G   [B H]
      H   [B G]

which representation to use?

adjacency matrix uses n² bits
adjacency list uses n + 2m node labels
worst case, m ∈ Θ( n² )
if n large and average degree small, lists smaller than matrix

graph traversal: depth first search

depth first search
def dfs(G):
  seen = {}
  for v in G: seen[v] = False
  for v in G:
    if not seen[v]:
      explore(G,v,seen)

def explore(G,v,seen):
  print v, 'start explore'
  seen[v] = True
  for nbr in G[v]:
    if not seen[nbr]:
      explore(G,nbr,seen)
  print v, 'finish explore'

def show(G):
  for v in sorted(G):
    print v,':',
    for j in G[v]: print j,
    print ''
  print ''

G = {'A': ['C', 'E', 'F'],
     'B': ['G', 'H'],
     'C': ['A', 'F'],
     'D': [],
     'E': ['A', 'F'],
     'F': ['A', 'C', 'E'],
     'G': ['B', 'H'],
     'H': ['B', 'G']}
show(G)
dfs(G)

output?
A start explore
C start explore
F start explore
E start explore
E finish explore
F finish explore
C finish explore
A finish explore
B start explore
G start explore
H start explore
H finish explore
G finish explore
B finish explore
D start explore
D finish explore

dfs traversal orders

preorder: by dfs start (1st encounter)
- A C F E B G H D
postorder: by dfs finish (last encounter)
- E F C A H G B D

components

components via dfs
def dfs(G):
  pre,post,seen,cmpt = {},{},{},{}
  for v in G:
    seen[v] = False
  clock, cnum  = [0], 0    #clock[0] passed by ref
  for v in G:
    if not seen[v]:
      cnum += 1
      explore(G,v,seen,pre,post,clock,cmpt,cnum)
  showall(G,pre,post,cmpt)

def explore(G,v,seen,pre,post,clock,cmpt,c):
  print 'explore from', v
  seen[v] = True
  cmpt[v] = c
  timestamp(v, pre, clock)
  for nbr in G[v]:
    if not seen[nbr]:
      explore(G,nbr,seen,pre,post,clock,cmpt,c)
  timestamp(v, post, clock)

def timestamp(v, order, clock):
  clock[0]+= 1; order[v] = clock[0]

def showall(G,pre,post,cnum):
  print '     ',
  for v in sorted(G): print '%2s' % v,
  print '\npre  ',
  for v in sorted(G): print '%2s' % pre[v],
  print '\npost ',
  for v in sorted(G): print '%2s' % post[v],
  print '\ncmpt ',
  for v in sorted(G): print '%2s' % cnum[v],

def show(G):
  for v in sorted(G):
    print v,':',
    for j in G[v]: print j,
    print ''
  print ''

G = {'A': ['C', 'E', 'F'],
     'B': ['G', 'H'],
     'C': ['A', 'F'],
     'D': [],
     'E': ['A', 'F'],
     'F': ['A', 'C', 'E'],
     'G': ['B', 'H'],
     'H': ['B', 'G'] }
show(G)
dfs(G)

traversal runtime

dfs runtime

adjacency matrix:
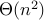
adjacency list:
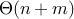
why? see text, then guess output from examples below

dfs list runtime example: output ?
def traverse(G):
  seen,cmpt,cnum,work = {},{},0,[0] #work reflects runtime
  for v in G:
    seen[v] = False
    cmpt[v] = 0
  for v in sorted(G):
    work[0] += 1
    if not seen[v]:
      cnum += 1
      dfs(G,v,seen,cmpt,cnum,work)
  print ''
  for v in sorted(G): print v,
  print ''
  for v in sorted(G): print cmpt[v],
  print '\nwork', work[0]

def dfs(G,v,seen,cmpt,c,work):
  seen[v],cmpt[v],work[0] = True,c,work[0]+1
  for nbr in sorted(G[v]):
    work[0] += 1
    if not seen[nbr]:
      dfs(G,nbr,seen,cmpt,c,work)
  print v,

def show(G):
  for v in sorted(G):
    print v,':',
    for j in G[v]: print j,
    print ''
  print ''

G = {'A': ['F'],
     'B': ['D','C'],
     'C': ['G','B','E','D'],
     'D': ['G','B','C'],
     'E': ['C','G'],
     'F': ['A'],
     'G': ['C', 'D']}

show(G)
traverse(G)

dfs matrix runtime example: output ?
def n(G): return len(G[0])
def alpha(j): return chr(j+ord('A'))

def traverse(G):
  seen,cmpt,cnum,work = {},{},0,[0]
  for v in range(n(G)):
    seen[v] = False
    cmpt[v] = 0
  for v in range(n(G)):
    work[0] += 1
    if not seen[v]:
      cnum += 1
      dfs(G,v,seen,cmpt,cnum,work)
  print ''
  for v in range(n(G)): print alpha(v),
  print ''
  for v in range(n(G)): print cmpt[v],
  print '\nwork', work[0]

def dfs(G,v,seen,cmpt,c,work):
  seen[v],cmpt[v],work[0] = True,c,work[0]+1
  for j in range(n(G)):  # possible nbr
    work[0] += 1
    if G[v][j]==1:     # j is nbr
      if not seen[j]:
        dfs(G,j,seen,cmpt,c,work)
  print alpha(v),

def show(G):
  print '   ',
  for v in range(n(G)): print alpha(v),
  print ''
  for v in range(n(G)):
    print alpha(v),':',
    for w in range(n(G)):
      if G[v][w]==1: print '1',
      else:          print '0',
    print ''
  print ''

G = ([0, 0, 0, 0, 0, 1, 0],
     [0, 0, 1, 1, 0, 0, 0],
     [0, 1, 0, 1, 1, 0, 1],
     [0, 1, 1, 0, 0, 0, 1],
     [0, 0, 1, 0, 0, 0, 1],
     [1, 0, 0, 0, 0, 0, 0],
     [0, 0, 1, 1, 0, 0, 0])

show(G)
traverse(G)

breadth first search

another graph
B - L - G   M   A
 \ / \ /     \ /
  I - E       H - K
   \ / \
    C - J - F - D

breadth first search
def bfs(G): # depth in bfs forest
  seen, depth = {}, {}
  for v in G:
    seen[v], depth[v] = False, 0
  print 'bfs order       ',
  for v in sorted(G):
    if not seen[v]:
      explorebfs(G,v,seen,depth)
  print '\nnodes           ',
  for v in sorted(G): print v,
  print '\nbfs forest depth',
  for v in sorted(G): print depth[v],
  print ''

def addtolist(L,v,seen):
  L.append(v); seen[v]=True

def explorebfs(G,v,seen,d):
  Q = []
  addtolist(Q,v,seen)
  while len(Q)>0:
    v = Q.pop(0); print v,
    for nbr in G[v]:
      if not seen[nbr]:
        d[nbr] = 1 + d[v]
        addtolist(Q,nbr,seen)

def show(G):
  for v in sorted(G):
    print v,':',
    for j in G[v]: print j,
    print ''

G = { 'A':['H'],
      'B':['I','L'],
      'C':['E','I','J'],
      'D':['F'],
      'E':['C','G','I','J','L'],
      'F':['D','J'],
      'G':['E','L'],
      'H':['A','K','M'],
      'I':['B','C','E','L'],
      'J':['C','E','F'],
      'K':['H'],
      'L':['B','E','G','I'],
      'M':['H']}

bfs(G)

directed graphs

arc list of a digraph
D = { 'A':['B'],
      'B':['C','E','F'],
      'C':['D','G'],
      'D':['C','H'],
      'E':['A','F'],
      'F':['G'],
      'G':['F'],
      'H':['D','G']
}

digraph lingo

scc pix
another another
arc
strongly connected: if, for each ordered pair of vertices (a,b), there is a path from a to b
strongly connected component:
- vertex subset
- the subset is strongly connected
- the subset is maximal (wrt being strongly connected)
transpose of a digraph: reverse direction of every arc
in a digraph
- source node/scc: has no in-arcs
- sink node/scc: has no out-arcs

strongly connected components

scc algorithm

to find sccs of digraph D:
- find node s in sink scc S
- find and remove S
- repeat until done
how to find s ?
- last in postorder of transpose T
how to find S?
- start from s, use dfs/bfs on D
runtime
- adjacency list
  - can find transpose in Θ(n+m) time
  - total Θ(n+m) time
- adjacency matrix
  - can find transpose in time Θ(n²)
  - total time Θ(n²)
correctness
- in acyclic digraph D postorder
  - each v appears after all w reachable from v, so
  - last vertex is D source, so
- in transpose T postorder
  - last vertex is T source, so
  - last vertex is D sink
- in postorder of transpose T of arbitrary digraph D,
  - last vertex is in D sink scc

strongly connected components
def dfs(G,v,seen,cmpt,c,S,phase):
  seen[v],cmpt[v] = True,c
  for nbr in sorted(G[v]):
    if not seen[nbr]: dfs(G,nbr,seen,cmpt,c,S,phase)
  if (phase==0): S.append(v) # append in postorder

def transpose(G):
  T = {}
  for v in G: T[v] = []
  for v in G:
    for w in G[v]: T[w].append(v)
  return T

def scc(G):
  phase,seen,cmpt,c,S = 0,{},{},0,[]
  for v in G: seen[v],cmpt[v] = False, 0
  T = transpose(G)
  for v in sorted(T):
    if not seen[v]: dfs(T,v,seen,cmpt,c,S,phase)
  showall(T,cmpt,S)

  phase,c = 1,0
  for v in G: seen[v],cmpt[v] = False, 0
  while len(S)>0:
    v = S.pop() # pop from end, so reverse order
    if not seen[v]:
      c += 1
      dfs(G,v,seen,cmpt,c,S,phase)
  showall(G,cmpt,S)

def showall(G,cmpt,S):
  print '     ',
  for v in sorted(G): print '%2s' % v,
  print '\ncmpt ',
  for v in sorted(G): print '%2s' % cmpt[v],
  print '\nstack', S

D = { 'A':['B'],
      'B':['C','E','F'],
      'C':['D','G'],
      'D':['C','H'],
      'E':['A','F'],
      'F':['G'],
      'G':['F'],
      'H':['D','G']
}

G = {'A':['F'],
     'B':['H'],
     'C':['B','F'],
     'D':['I'],
     'E':['B'],
     'F':['C','I'],
     'G':['E'],
     'H':['G'],
     'I':['A','G']}
scc(D)

scc example: part I

a digraph D

a digraph D

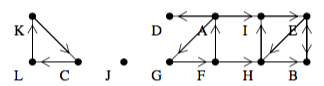
its transpose T

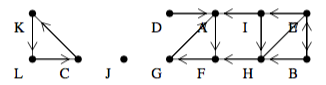
its transpose T

scc example: part II
D dfs traversal forest:

  A         C       J
D   G       L
    F       K
    H
  B   I
  E

D-dfs postorder
D E B I H F G A  K L C  J

notice:
postorder-first node in  sink  scc (why?)
postorder-last  node in source scc (why?)

T dfs traversal forest:

  A     B     C     D    J
  F     E     K
  G     I     L
        H

T-dfs postorder
G F A  H I E B  L K C  D  J

G dfs traversal forest, using reverse T postorder:

   J   D   C   B   A
           K   E   F
           L   I   G
               H

notice:
each tree in above forest is scc of T/D

scc exercise

how do the results of scc(D) compare with scc(transpose(D)) ?
try an example or two
explain