coping with NP-C

exhaustive search   backtrack   sat solver   2-sat   phase transition  

exhaustive tree search (ETS)

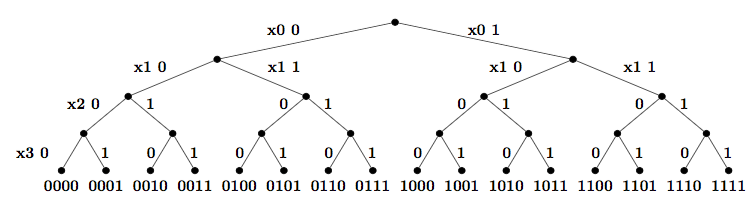
  • common form of exhaustive search: traverse a decision tree

  • tree search: traversal of search space based on a decision tree

  • e.g. sat: choice 0/1 for each boolean variable

    • left branch of node at depth k: variable k = 0

    • left branch of node at depth k: variable k = 1

  • usually, depth first traversal

  • in memory, only need path from root to current node

  • example below for n = 4, variables x0 x1 x2 x3

example: tree search of sat instance, n=4

decision tree search

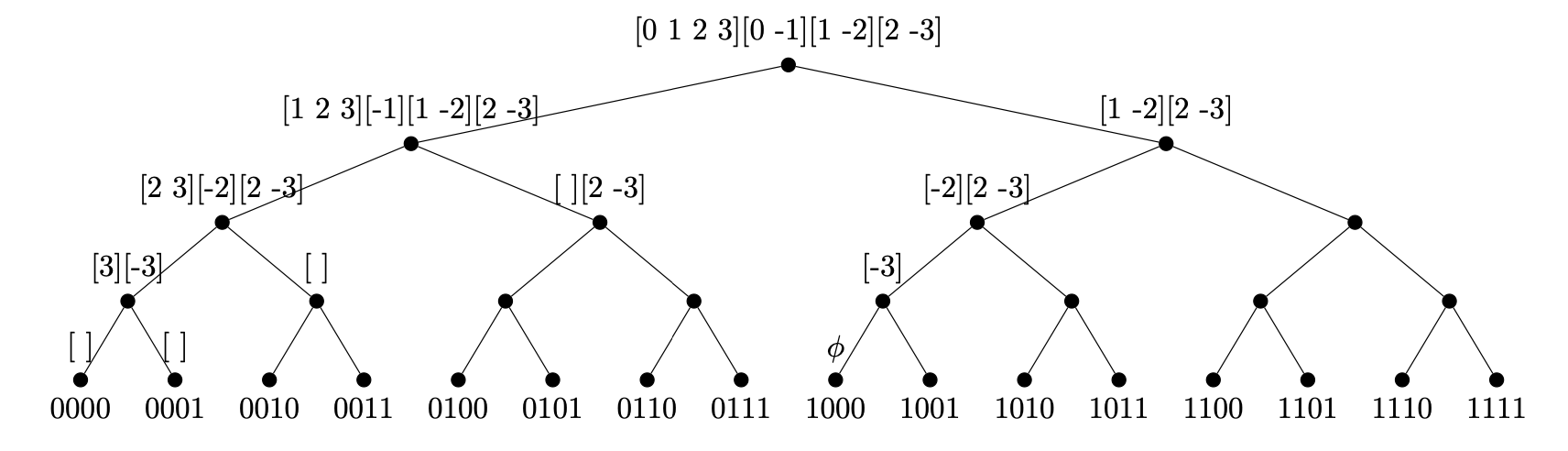
intelligent ETS: backtracking

how to make ETS intelligent ?

  • with no improvements, WC, whole tree traversed

  • how to avoid searching whole tree?

    • backtrack when current node cannot extend to solution

  • example below for n = 4, variables x0 x1 x2 x3

  • initialize formula f, say [0 1 2 3] [0 -1] [1 -2] [2 -3]

  • loop

    • if f has 0 clauses, return SAT

    • if some clause has 0 literals, return UNSAT

    • pick next variable not yet set, say x

    • for L in { x, -x } : # set x = True, x = False

      • if L in c, remove c from f

      • if -L in c, remove x from c

sat solvers

example: backtrack sat solver

backtrack sat solve

more intelligent exhaustive search

  • use current partial solution to pick next search step

more intelligent sat solver

  • use current reduced formula to pick next variable to set

    • e.g. if some clause has size 1, set variable so clause sat

    • more generally: set variable from any shortest clause

  • improving sat solvers is continuing research area

  • classic sat solver DPLL

    • unit propagation

    • pure literal elimination

  • best sat solvers still wc exptime

  • below: simple sat solver

    • set variable from any shortest clause

    • backtrack once some clause unsat

simple backtrack sat solver
def sat(f): return (True if len(f)==0 else False)
def unsat(a): return (True if a[0]==UNSAT else False)

def backsat(f,a):
  if unsat(a) or sat(f): return f,a
  minj = f.index(min(f,key=len))  # clause with fewest literals
  if len(f[minj])==0:
    a[0] = UNSAT
    return f,a
  if len(f[minj])==1:
    fixliteral(f[minj][0], f, a)
    return backsat(f,a)
  #split: 2 possible bool. vals for literal f[minj][0]
  fcopy, acopy = mycopy(f,a)
  fixliteral(f[minj][0], f, a)  # f[minj][0] True
  f,a = backsat(f,a)
  if sat(f): return f, a
  f,a = fcopy, acopy
  fixliteral(-f[minj][0], f, a) # f[minj][0] False
  return backsat(f, a)
time?

  • above solves random n, k, m = 30, 5, 600 instance in few seconds, while brute force takes much longer (why?)

restricted instances can be easier

  • e.g. knapsack, each value/wt has O(logk n) bits, polytime

  • e.g. 2-sat?

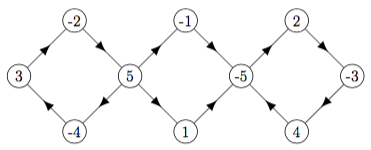
    • f1 = [[1,-5],[-2,-3],[3,4],[-4,-5],[2,5],[-1,-5]] satisfiable ?

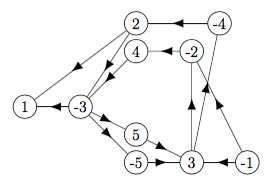
    • f2 = [[1,-2],[1,3],[-2,-3],[2,4],[-3,-4],[3,-5],[3,5]] satisfiable ?

polytime 2-sat via implication digraph

implication digraph of 2-sat formula

  • one node for each literal

  • for each clause [a,b]

    • draw arc from literal negate(a) to literal b

    • draw arc from literal negate(b) to literal a

  • e.g. formula f1 below

    • nodes (1) (2) (3) (4) (5) (-1) (-2) (-3) (-4) (-5)

    • clause [1 -5]     (-1) ----> (-5)       (1) <---- (5)

    • clause [-2 -3]     (2) ----> (-3)       (-2) <---- (3)

    • ...

f1 [1 -5] [-2 -3] [3 4] [-4 -5] [2 5] [-1 -5]

implication digraph f1

f2 [1 -2] [1 3] [-2 -3] [2 4] [-3 -4] [3 -5] [3 5]

implication digraph f2

2-sat in P

  • n variables, m clauses

  • construct implication digraph D

  • if some scc of D contains literal x and -x then unsat (why ?)

  • otherwise

    • consider sink scc S of D

    • assign literals according to S (no inconsistencies: why ?)

    • remove S, and all variables in S, from D

    • continue with remaining digraph D'

  • this algorithm takes polytime (why ?)

  • this algorithm correct (why ?)

example f1

  • f1 has sccs {-2 5 -4 3} {-1} {1} {2 -3 4 -5}

  • no scc contains both x and -x, so f1 satisfiable

  • sink scc {2 -3 4 -5} so set 2T 3F 4T 5F

  • from digraph, remove this scc and all instances of variables 2 3 4 5

  • remaining digraph has sccs {-1} {1}

  • each is sink scc, so pick either, assign 1F or 1T

example f2

  • f1 has sccs {-1} {-2 2 -3 3 -4 4 -5 5} {1}

  • some scc contain both x and -x, so f2 unsatisfiable

3-sat phase transition

  • if clause/variable ratio m/n small, say ≤ 3

    • Prob(sat) close to 1

    • easy to solve

  • if clause/variable ratio m/n big, say ≥ 5

    • Prob(sat) close to 0

    • easy to solve

  • if clause/variable ratio m/n ≈ 4.2

    • Prob(sat) close to .5

    • hardest to solve

  • see p3

  • easy-hard-easy common to NP-C