AIxploratorium
Decision Trees
 

Modifications to the LearnDT algorithm

[[This page is still being written. It will be completed soon!]]

Many Learning Algorithms: Why use InformationGain? Or even GainRatio? Yes, they do try to find the smallest decision tree, which is sometimes useful (see Occam). But there remain several issues: First, it is not clear that the smallest tree really is the most accurate. (see No Free Lunch). Second, even if the smallest really is best, our specific algorithm does not always find the absolute smallest, as it is only GREEDILY hill-climbing. (Note that finding the smallest is NP hard.) The third, and most damning, problem is that our learner is only using a SAMPLE of the instances (here, of the games), which may not be representative of the true distributions. For example, perhaps the MallRats will almost always lose away games where Fred starts and Joe plays center (both offense and defense). But in the one such game we actually saw, they just happen to win. (This is like flipping a 0.99-head coin, and getting tails.)

The pruning idea attempts to address this. There have been a variety of other "tweaks", towards addressing this. These include

  • learning a set of decision trees, based on different samples. See Four Current Trends

  • Use some other splitting criteria. From Article, there are several obvious criteria for splitting functions:
    • the best score should be for a distribution of the form [1,0,0,0]
    • the worst score should be for a distribution of the form [1/4, 1/4, 1/4, 1/4] and
    • the measure should be symmetric --- ie, the same for [0.3, 0.1, 0, 0.6] as for [0.1, 0, 0.6, 0.3], etc.

    Note that both InformationGain and GainRatio satisfy these properties. Another measure is GINI measure

    Gini(A) = 1 - sum_i p_i ^2

    You can try this out: In the applet, reset the "Split Function" pull-down menu to "GINI".

    (Other measures include "Statistical Chi2 test", "Marshall Correction", "G statistic", ...)

  • Try other PRUNING functions; see Other Pruners

Note: many researchers have found that the splitting criteria is not that useful, but pruning is essential. For that reason, essentially all decision tree learners include some pruning facility.


  • Each classifier has an associated "decision boundary", which separate the different classes. To introduce this idea, consider the far-simpler learning problem: Who is bald, given the person's gender (from {Male, Female}) and age range (from {Baby, Child, Teenager, Adult, OldAdult}), and imagine our data looks like this:
    Gender Age Bald
    Male Baby No
    Male Teenager No
    Female OldAdult No
    Female Teenager No
    Male OldAdult Yes

    We could graph this: using each attribute on an axis, each instance corresponds to a point. We could then put a BOX ([]) on each point representing a positive instance (ie, a bald person), and a circle (o) on each negative instance:

    [Produce this graph!]

    This graph also includes a line that separates the positive from the negative instances.

    Here, we drew a straight line. The obvious decision tree, here, would be

    [Draw this tree!]

    Its "decision surface" is a bit more complicated, as it first splits based on age, and then, for certain ages, further divides, based on gender:

    [Produce this revised graph!]

    Notice the decision boundary, here, is composed of a series of axis-parallel segments. This is true of decision-trees in general.

    Now recall our basketball example: Here, each instances corresponds to a point in a 6-dimensional "instance" space, as each instance has a "Where" value (either Home or Away) a "When" value (one of 5pm, 7pm or 9pm), a "Fred Starts" value (either Yes or No), etc. (As each game corresponds to exactly one of these, there are 2*3*2*2*2*2=96 possible types of games. Of course, several different games could have the same description.) Each of the decision trees considers again corresponds to a sequence of such axis-parallel "hyper-planes".

    Another approach is to consider "oblique" trees. See Salzberg, Kasif, ...

  • Why not MANY different decision trees, averaged together

    [[to be completed]]

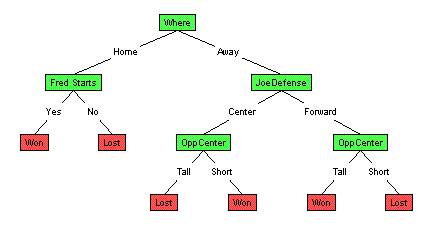
  • This algorithm is greedy --- trying to find the single split that most improves things. What if no single split effective --- eg, XOR. Here, there is NO advantage to a single split, but with 2 splits, we can be perfect. In fact, that is true for our current situation;

    Note the lower left is the exclusive-or of "OppC=Tall (+) JoeDefense=Center".

    [[to be completed]]

    Actually there is a yet-smaller tree. Can you find it?

    		•
     
    Commercial Successes Decision Trees Other Models